Кристаллы. Элементы кристаллографии
· Молярный объем кристалла
Vm = M/r,
где М — молярная масса вещества; r — плотность кристалла. Объем V элементарной ячейки в кристаллах:
а) при кубической сингонии V = a3;
б) при гексагональной сингонии 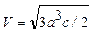 . Здесь а и с — параметры решетки.
. Здесь а и с — параметры решетки.
Если для гексагональной решетки принять теоретическое значение
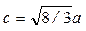 , то
, то 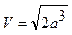 .
.
· Число Zm элементарных ячеек в одном моле кристалла
Zm = Vm/v, или Zm = kNA/n,
где k — число одинаковых атомов в химической формуле соединения (например, в кристалле AgBr число одинаковых атомов Ag или Вг в химической формуле соединения равно единице); NA — постоянная Авогадро; п— число одинаковых атомов, приходящихся на элементарную ячейку. Число Z элементарных ячеек в единице объема кристалла
Z = Zm/Vm
или в общем случае
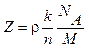
для кристалла, состоящего из одинаковых атомов (k = l),
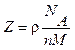
· Параметр а кубической решетки
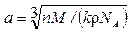
Расстояние d между соседними атомами в кубической решетке:
а) в гранецентрированной 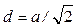 ,
,
б) в объемно центрированной 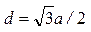 .
.
Электроны в металле (по квантовой статистике)
Распределение Ферми по энергиям для свободных электронов в металле:
при Т¹0 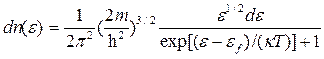 ;
;
при Т¹0 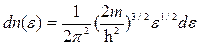 при (e<ef),
при (e<ef),
где dn(e)-концентрация электронов, энергия которых заключена в интервале, значений от e до e+de; m и e - масса и энергия электрона; eƒ- уровень (или энергия) Ферми.
Уровень Ферми в металле при Т=0
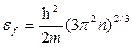 .
.
Температура Ткр вырождения
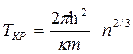 .
.
Удельная проводимость собственных полупроводников
g = en(bn + bp),
где e - заряд электрона; n - концентрация носителей заряда (электронов и дырок); bn и bp - подвижности электронов и дырок.
Напряжение UH на гранях образца при эффекте Холла
UH = RHBjℓ,
где RH - Постоянная Холла; В - индукция магнитного поля;
ℓ - ширина пластины; j - плотность тока.
Постоянная Холла для полупроводников типа алмаза, кремния; германия и др., обладающих носителями заряда одного вида (n или р),
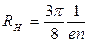 ,
,
где n - концентрация носителей заряда.
Примеры решения задач
Пример 1. В баллоне вместимостью V=6,9 л находится азот массой m=2,3 г. При нагревании часть молекул диссоциировали на атомы. Коэффициент диссоциации a=0,2. Определить: 1) общее число N1 молекул и концентрацию n1 молекул азота до нагревания; 2) концентрацию n2 молекул и n3 атомов азота после нагревания.
Решение. По определению, концентрация частиц газа есть отношение числа частиц к вместимости сосуда, занимаемого газом:
n=N/V. (1)
1. Число N1 молекул газа до нагревания найдем из соотношения
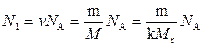 . (2)
. (2)
где v — количество вещества азота; na — постоянная Авогадро; М — молярная масса азота; Mr — относительная молекулярная масса азота; k=10-3 кг/моль. Подставив значения величин в (2), получим
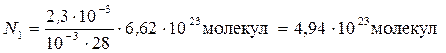 .
.
Концентрацию n1 найдем, подставив значения величин в (1):
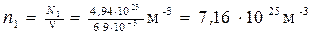 .
.
2. Концентрацию после нагревания найдем из соотношения
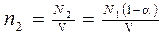 , (3)
, (3)
где N — число молекул, не распавшихся на атомы.
После подстановки значений величин в (3) получим
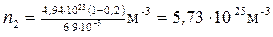 .
.
Концентрация атомов после нагревания азота
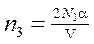 . (4)
. (4)
Число 2 в формуле (4) выражает тот факт, что каждая молекула после распада дает два атома.
Подставим в (4) значения величин и произведем вычисления:
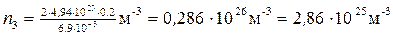 .
.
Пример 2. В колбе вместимостью V=0,5 л находится кислород при нормальных условиях. Определить среднюю энергию 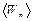 поступательного движения всех молекул, содержащихся в колбе.
поступательного движения всех молекул, содержащихся в колбе.
Решение. Средняя энергия 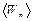 поступательного движения всех молекул может быть выражена соотношением
поступательного движения всех молекул может быть выражена соотношением
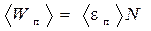 , (1)
, (1)
где <eп>— средняя энергия поступательного движения одной молекулы; N — число всех молекул, содержащихся в колбе.
Как известно,
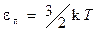 , (2)
, (2)
где k — постоянная Больцмана; Т — термодинамическая температура.
Число молекул, содержащихся в колбе, найдем по формуле
N=vNA, (3)
где v — количество вещества кислорода; NA — постоянная Авогадро.
Количество вещества v найдем из таких соображений: известно, что при нормальных условиях молярный объем Vm равен 22,4×10-3 м3/моль. Так как, по условию задачи, кислород в колбе находится при нормальных условиях, то количество вещества кислорода в колбе выражается соотношением
v=V/Vm. (4)
Подставив выражение v по (4) в (3), получим
N=VNA/Vm. (5)
С учетом (2) и (5) выражение (1) энергии поступательного движения молекул примет вид
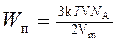
Проверим, дает ли правая часть расчетной формулы единицу энергии (джоуль). Для этого вместо символов величин подставим единицы, в которых эти величины выражаются:
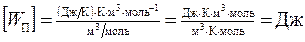 .
.
Подставив значения величин в (6) и произведя вычисления, найдем
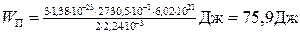 .
.
Пример 3. Средняя длина свободного пробега <l> молекулы углекислого газа при нормальных условиях равна 40 нм. Определить среднюю арифметическую скорость <J> молекул и число z соударений, которые испытывает молекула в 1 с.
Решение. Средняя арифметическая скорость молекул определяется по формуле
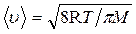 ,
,
где М — молярная масса вещества.
Подставив числовые значения, получим
<υ>=362 м/с.
Среднее число <z> соударений молекулы в 1 с определяется отношением средней скорости <υ> молекулы к средней длине ее свободного пробега <l>:
<z>=<υ>/<l>.
Подставив в эту формулу значения <υ>=362 м/с, <l>=40 нм=4×10-8 м, получим
<z>= 9,05×109 с-1.
Пример 4. Два тонкостенных коаксиальных цилиндра длиной l= 10 см могут свободно вращаться вокруг их общей оси z. Радиус Rбольшого цилиндра равен 5 см. Между цилиндрами имеется зазор размером d=2 мм. Оба цилиндра находятся в воздухе при нормальных условиях. Внутренний цилиндр приводят во вращение с постоянной частотой n1=20 с-1. Внешний цилиндр заторможен. Определить, через какой промежуток времени с момента освобождения внешнего цилиндра он приобретет частоту вращения n2=1c-1. При расчетах изменением относительной скорости цилиндров пренебречь. Масса m внешнего цилиндра равна 100 г.
Решение. При вращении внутреннего цилиндра слой воздуха увлекается им и начинает участвовать во вращательном движении. Вблизи поверхности этого цилиндра слой воздуха приобретает со временем практически такую же линейную скорость, как и скорость точек на поверхности цилиндра, т. е. υ=2pn1(R – d). Так как d«R, то приближенно можно считать
υ»2pn1R (1)
Вследствие внутреннего трения момент импульса передается соседним слоям газа и в конечном счете внешнему цилиндру. За интервал времени Dt внешний цилиндр Приобретает момент импульса L=pR, где р — импульс, полученный за Dt внешним цилиндром. Отсюда
p=L/R. (2)
С другой стороны,
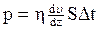 , (3)
, (3)
где h — динамическая вязкость; 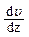 —градиент скорости; S —площадь поверхности цилиндра (S=2pRl).
—градиент скорости; S —площадь поверхности цилиндра (S=2pRl).
Приравняв правые части выражений (2) и (3) и выразив из полученного равенства искомый интервал Dt, получим
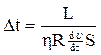 .
.
Найдем входящие в эту формулу величины L, 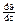 и S. Момент импульса L=Jw2, где J — момент инерции цилиндра (J=mR2); m — его масса; w2 — угловая скорость внешнего цилиндра (w2=2pn2). С учетом этого запишем
и S. Момент импульса L=Jw2, где J — момент инерции цилиндра (J=mR2); m — его масса; w2 — угловая скорость внешнего цилиндра (w2=2pn2). С учетом этого запишем
L=mR2×2pn2=2pmR2n2
Градиент скорости 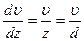 .Площадь цилиндра равна S=2pRl.
.Площадь цилиндра равна S=2pRl.
Подставив в (4) выражения L, 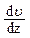 , S, получим
, S, получим
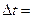
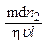 .
.
Заменив здесь υ по (1), найдем
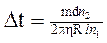 . (5)
. (5)
Динамическая вязкость воздуха h== 17,2 мкПа×с= 1,72∙10-5 Па∙с.
Подставив в (5) значения входящих в нее величин и произведя вычисления, получим
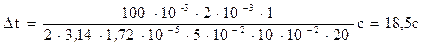 .
.
Пример 5. Найти среднюю кинетическую энергию одной молекулы аммиака NH3 при температуре t=27 °С и среднюю энергию вращательного движения этой молекулы при той же температуре.
Решение. Средняя полная энергия молекулы определяется по формуле
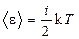 (1)
(1)
где i — число степеней свободы молекулы; k — постоянная Больцмана; Т—термодинамическая температура газа: T=t+Т0, где Т0=273 К.
Число степеней свободы i четырехатомной молекулы, какой является молекула аммиака, равно 6.
Подставим значения величин в (l):
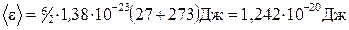 .
.
Средняя энергия вращательного движения молекулы определяется по формуле
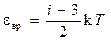 , (2)
, (2)
где число 3 означает число степеней свободы поступательного движения.
Подставим в (2) значения величин и вычислим:
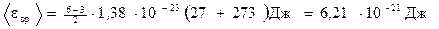 .
.
Заметим, что энергию вращательного движения молекул аммиака можно было получить иначе, разделив полную энергию (e) на две равные части. Дело в том, что у трех (и более) атомных молекул число степеней свободы, приходящихся на поступательное и вращательное движение, одинаково (по 3), поэтому энергии поступательного и вращательного движений одинаковы. В данном случае
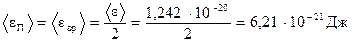
Пример 6. Пылинки массой m=10-18 г взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1 %. Температура Т воздуха во всём объеме одинакова и равна 300 К.
Решение. При равновесном распределении пылинок концентрация их зависит только от координаты z по оси, направленной вертикально. В этом случае к распределению пылинок можно применить формулу Больцмана
n=n0e-U/(kT). (1)
Так как в однородном поле силы тяжести U=mgz, то
n=n0e-mgz/(kT) (2)
По условию задачи, изменение Dn концентрации с высотой мало по сравнению с n (Dn/n=0,01), поэтому без существенной погрешности изменение концентрации Dn можно заменить дифференциалом dn.
Дифференцируя выражение (2) по z, получим
dп= —п0 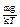 e-mgz/(kT)dz.
e-mgz/(kT)dz.
Так как п0e-mgz/(kT)=n, то
dn= - 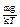 ndz.
ndz.
Отсюда находим интересующее нас изменение координаты:
dz= - 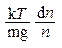
Знак минус показывает, что положительным изменениям координаты (dz>0) соответствует уменьшение относительной концентрации (dn<0). Знак минус опустим (в данном случае он несуществен) и заменим дифференциалы dz и dn конечными приращениями Dz и Dn:
Dz = 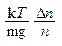 .
.
Подставим в эту формулу значения величин Dn/n=0,01, k=1,38×10-23 Дж/К, T=300 К, m= 10-21 кг, g=9,81 м/с2 и, произведя вычисления, найдем
Dz=4,23 мм.
Как видно из полученного результата, концентрация даже таких маленьких пылинок (m== 10-18 г) очень быстро изменяется с высотой.
Пример 7. В сосуде содержится газ, количество вещества v которого равно 1,2 моль. Рассматривая этот газ как идеальный, определить число DN молекул, скорости υ которых меньше 0,001 наиболее вероятной скорости υв.
Решение. Для решения задачи удобно воспользоваться распределением молекул по относительным скоростям u (u=υ/υв). Число dN(u) молекул, относительные скорости и, которых заключены в пределах от u до du, определяется формулой
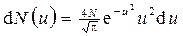 , (1)
, (1)
где N — полное число молекул.
По условию задачи, максимальная скорость интересующих нас молекул υmax=0,001υв, откуда umax=υmax/υв=0,001. Для таких значений и выражение (1) можно существенно упростить. В самом деле, для u«1 имеем е-2»1-u2. Пренебрегая значением u2=(0,001)2=10-6 по сравнению с единицей, выражение (1) запишем в виде
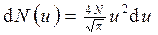 . (2)
. (2)
Интегрируя это выражение по и в пределах от 0 до umax, получим
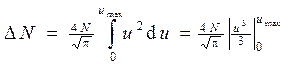 , или
, или 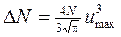 . (3)
. (3)
Выразив в (3) число молекул N через количество вещества и постоянную Авогадро, найдем расчетную формулу:
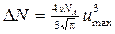 . (4)
. (4)
Подставим в (4) значения величин v, na и произведем вычисления:
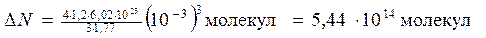 .
.
Пример 8. Зная функцию f(р) распределения молекул по импульсам, определить среднее значение квадрата импульса <p2>.
Решение. Среднее значение квадрата импульса <p2> можно определить по общему правилу вычисления среднего:
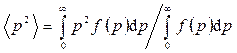 . (1)
. (1)
Функция распределения молекул по импульсам имеет вид
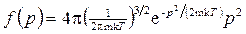 (2)
(2)
Эта функция распределения уже нормирована на единицу, т. е.
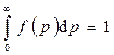 .
.
С учетом нормировки формулу (1) перепишем иначе:
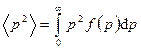 (3)
(3)
Подставим выражение f(p) по уравнению (2) в формулу (3) и вынесем величины, не зависящие от р, за знак интеграла:
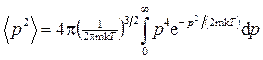
Этот интеграл можно свести к табличному.
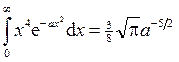 , положив
, положив 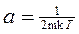 .
.
В нашем случае это даст
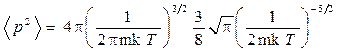
После упрощений и сокращений найдем
<p2>=3mkT.
Пример 9. Определить количество теплоты DQ, необходимое для нагревания кристалла NaCI массой m=20г на DТ=2К, в двух случаях, если нагревание происходит от температуры: 1) T1=qВ; 2) Т2=2К. Характеристическую температуру Дебая qD для NaCI принять равной 320 К.
Решение. Количество теплоты DQ, подводимое для нагревания тела от температуры t1 до t2, Может быть вычислено по формуле
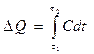 , (1)
, (1)
где С - теплоемкость тела (системы)
Теплоемкость тела связана с молярной теплоёмкостью Cm соотношением С=(m/М) Cm, где m-масса тела; М-молярная масса. Подставив это выражение С в формулу (1), получим
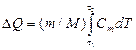 . (2)
. (2)
В общем случае Cm есть функция температуры, поэтому за знак Интеграла ее выносить нельзя. Однако в первом случае изменением теплоемкости по сравнению с ее значением при температуре Т, можно пренебречь и считать ее на всем интервале температур DT постоянной и равной Cm(Т1). Ввиду этого формула (2) примет вид
DQ=(m/M)Cm(Т1)DT. (3)
Молярная теплоёмкость Cm(Т1) в теории Дебая выражается формулой
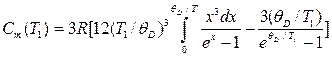 .
.
В первом случае при Т1=q интеграл
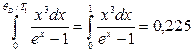
и, следовательно,
Cm =2,87R.
Подставляя это значение Cm в формулу (3),получим
DQ=2,87(m/M)RDT. (4)
Произведя вычисление по формуле (4), найдём
DQ=16,3Дж.
Во втором случае (Т<<qD) нахождение DQ облегчается тем, что можно воспользоваться предельным законом Дебая, в согласии с которым теплоемкость пропорциональна кубу абсолютной температуры. В этом случае теплоемкость сильно изменяется в пределах заданного интервала температур и ее нельзя выносить за знак интеграла в формуле (2)
Используя выражение предельного закона Дебая
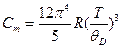 ,
,
получим
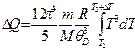
Выполним интегрирование:
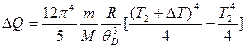 . (5)
. (5)
С учетом того, что Т2+DТ=2Т2, выражение (5) примет вид
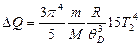 ,
,
или
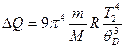 .
.
Подставив в последнюю формулу значения величин p, m, M, R, Т и qВ произведя вычисления, найдём DQ=1,22мДж.
Пример 10.Молярная изохорная теплоемкость аргона при температуре 4 К равна 0,174 Дж/(моль∙К). Определить значение молярной изохорной теплоемкости аргона при температуре 2 К.
Решение.Согласно теории Дебая, теплоемкость кристаллической решетки при низких температурах Т, когда Т<<θD, где θD – характеристическая температура Дебая, пропорциональна кубу термодинамической температуры,
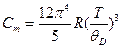 . (1)
. (1)
При высоких температурах, когда Т>>θD, теплоемкость кристаллической решетки описывается законом Дюлонга и Пти
С=3R=25 Дж/(моль∙К). (2)
Так как при Т1=4 К теплоемкость аргона С1=0,174 Дж/(моль∙К) много меньше, чем 3R=25 Дж/(моль∙К), выполняется закон Т3 Дебая, согласно которому
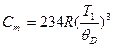 ,
, 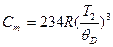 , (3)
, (3)
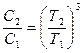
или
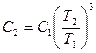 . (4)
. (4)
Подставляя числовые данные в (4), получим
С2=0,022 Дж/(моль∙К).
Пример 11.Дебаевская температура кристалла равна 150 К. Определить максимальную частоту колебаний кристаллической решетки. Сколько фотонов такой же частоты возбуждается в среднем в кристалле при температуре 300 К.
Решение.Дебаевская температура
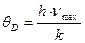 , (1)
, (1)
где νmax – максимальная частота колебаний кристаллической решетки, h=6,625∙10-34 Дж∙с, k=1,38∙10-23Дж/К – постоянная Больцмана.
Из (1) найдем
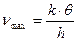 . (2)
. (2)
Подставляя в (2) числовые значения, получаем
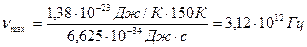 .
.
Среднее число фотонов с энергией εi:
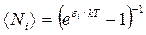 . (3)
. (3)
Энергия фотона, соответствующая частоте колебаний νmax,
εi=h∙ν=k∙θD. (4)
Подставляя (4) в (3),
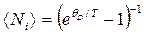 ,
,
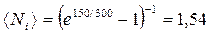 .
.
Пример 12. Определить число п узлов, приходящихся на одну элементарную ячейку в гранецентрированной кубической решетке.
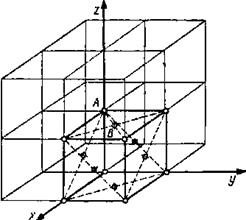 Решение. Выделим элементарную ячейку в кубической решетке (рис. 1) и определим, скольким соседним элементарным ячейкам принадлежит тот или иной узел выделенной ячейки. В этой ячейке имеются узлы двух типов: А (находящиеся в вершинах куба) и В (находящиеся на гранях куба в точке пересечения диагоналей).
Решение. Выделим элементарную ячейку в кубической решетке (рис. 1) и определим, скольким соседним элементарным ячейкам принадлежит тот или иной узел выделенной ячейки. В этой ячейке имеются узлы двух типов: А (находящиеся в вершинах куба) и В (находящиеся на гранях куба в точке пересечения диагоналей).
Узел А принадлежит одновременно восьми элементарным ячейкам. Следовательно, в данную ячейку узел А входит с долей 1/8. Узел В входит одновременно только в две ячейки и, следовательно, в данную ячейку узел В входит с долей 1/2. Если учесть, что число узлов
типа А в ячейке равно восьми, Рис. 1
а число узлов типа В равно шести, т. е. числу граней, то общее число узлов, приходящихся на одну элементарную ячейку в гранецентрированной решетке,
n = (1/8)×8 + (1/2)×6 = 1 + 3 = 4 узла.
Так как число узлов равно числу атомов, то в соответствующей структуре на элементарную ячейку приходится четыре атома.
Пример 13. Определить параметр а решетки и расстояние d между ближайшими соседними атомами кристалла кальция (решетка гранецентрированная кубической сингонии). Плотность r кристалла кальция равна 1,55×103 кг/м3.
Решение. Параметр а кубической решетки связан с объемом элементарной ячейки соотношением V = а3. С другой стороны, объем элементарной ячейки равен отношению молярного объема к числу элементарных ячеек в одном моле кристалла: V = Vm/Zm. Приравняв правые части приведенных выражений для V найдем
a3 = Vm/Zm (1)
 Молярный объем кальция Vm = M/r, где r — плотность кальция; М — его молярная масса. Число элементарных ячеек в одном моле
Молярный объем кальция Vm = M/r, где r — плотность кальция; М — его молярная масса. Число элементарных ячеек в одном моле
Zm =NA/n,
где п — число атомов, приходящихся на одну ячейку. Подставив в формулу (1) приведенные выражения для Vm и Zm, получим
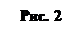 a3= nM/(rNA)
a3= nM/(rNA)
Отсюда
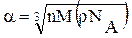 (2)
(2)
Подставим значения величин п, М, r и NA в формулу (2), учитывая, что п = 4 . Произведя вычисления, найдем
а =556 пм.
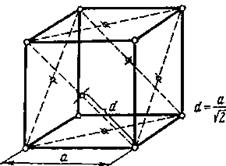
Расстояние d между ближайшими соседними атомами находится из простых геометрических соображений, ясных из рис. 2:
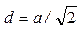 .
.
Подставив в это выражение найденное ранее значение а, получим d=393 пм.
Пример 14. Кусок металла объёма V=20 см³ находится при температуре Т=0. Определить число ΔN свободных электронов, импульсы которых отличаются от максимального импульса рmax не более чем на 0,1 рmax. Энергия Ферми eƒ=5эВ.
Решение. Для того чтобы установить распределение свободных электронов в металле по импульсам, воспользуемся распределением Ферми для свободных электронов при T=0:
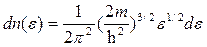 (1)
(1)
Так как dn(e) есть число электронов в единице объема, энергии которых заключены в интервале значений от e до e+de (e<eƒ), то оно должно быть равно числу электронов dn(p) в единице объема, заключённых в интервале значений импульса от р до p+dp, т. е.
dn(р)=dn(e). (2)
При этом должно соблюдаться следующее условие. Данной энергии e соответствует определенный импульс р(eƒ=p²(2m)) и интервалу энергий de отвечает соответствующий ему интервал импульсов
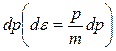 .
.
Заметив, что e1/2=p/(2m)1/2, подставим в правую часть равенства (2) вместо dn(e) выражение (1) с заменой e на р и
de на dp в соответствии с полученными соотношениями, т. е.
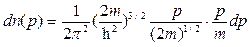 .
.
После сокращений получим искомое распределение свободных электронов в металле по импульсам при Т=0:
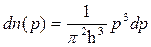 .
.
Число электронов в единице объема, импульсы которых заключены в интервале от рmax –0,1 рmax до рmax, найдем интегрированием в соответствующих пределах:
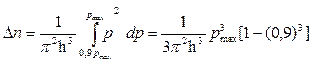 , или
, или 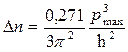 .
.
Учитывая, что максимальный импульс рmax и максимальная энергия e электронов и металле (при Т=0) связаны соотношением р²max=2meƒ, найдём искомое число ΔN свободных электронов в металле:
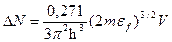 , или
, или 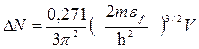 ,
,
Подставив значения величин p, m, eƒ, ћ и V и произведя вычисления (5эВ=8·10-19Дж), получим ΔN=2,9·1023 электронов.
Таблица вариантов
