Описание экспериментальная установки
Установка (рис.2) состоит из металлического баллона 1 который может быть соединен клапаном 4 либо с насосом 2 и манометром 3 , либо клапаном 5 с атмосферой. Водяной U-образный манометр измеряет разность между давлением в баллоне и атмосферном давлением в мм в.ст.
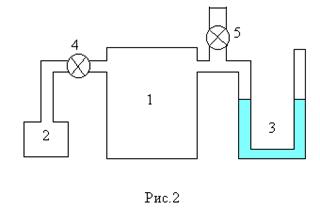 |
Рис.3 |
Вывод рабочей формулы
Выберем мысленно в баллоне объем воздуха массой m0 вдали от клапана. Назовем массу m0 рабочей массой газа. Эта масса останется все время в баллоне. Накачиваемый и выпускаемый из баллона воздух служит лишь для сжатия и расширения объема рабочей массы газа.
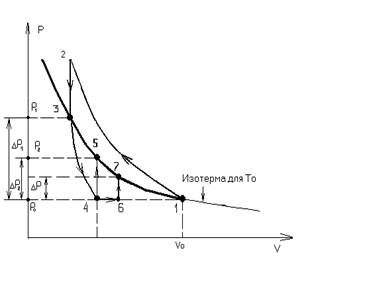
Для определения отношения теплоемкостей g воздуха находящегося в баллоне рассмотрим последовательность термодинамических процессов представленных на р - V - диаграмме (рис. 3). Обозначим через р0, V0, T0 исходные величины термодинамических параметров газа в баллоне (на диаграмме точка 1). Сначала в баллон накачивается воздух (процесс 1 - 2). При этом газ в баллоне сжимается и нагревается. После изохорного остывания до начальной комнатной температуры (процесс 2 - 3) газ имеет некоторое давление р1 и температуру Т0 (в точке 3 имеем параметры: р0,Т1,V). Затем газ адиабатически расширяется (процесс 3 - 4), т.к. баллон клапаном 5 соединяют с атмосферой. Газ при этом охлаждается и его давление падает до величины р0, а температура Т1 < Т0. В момент достижения давления р0 клапан должен перекрываться, и далее, газ будет изохорически нагреваться до комнатной температуры (процесс 4 - 5). В точке 5 давление газа р2 > р0, а температура равна Т0. В условиях реального эксперимента процесс (4-5) трудно осуществим, т.к. клапан баллона должен быть перекрыт в момент, когда давление в баллоне станет равным р0. С другой стороны время, в течение которого давление в баллоне уменьшается от р1 до р0, должно быть достаточно мало так, чтобы теплообменом с окружающем воздухом можно было бы пренебречь. Обозначим Δр1 = р1−р0 и Δр2 = р2−р0. Будем считать, что Δр1 << р0 и Δр2 << р0.
Рассмотрим влияние времени t, в течение которого клапан оставался открытым после достижения давления р0, на результат опыта. За это время t, пока клапан открыт, происходит изобарический нагрев (процесс 4 - 6) за счет теплообмена газа со стенками баллона, а также уход части газа из баллона, вызванный нагревом и расширением этого газа. Величину t назовем временем задержки.
После того, как клапан закрывается (6), происходит изохорический нагрев (процесс 6 - 7). Давление в баллоне достигает величины р0 + Δр. Конечное состояние (точка 7) лежит на той же изотерме, что и точки 1, 3, 5, но Δр ≠ Δр1 (Δр < Δр1).
Из этого рассмотрения видно, что Δр зависит от t. Таким образом, необходимо принять во внимание теплообмен и уход части газа из баллона за время t.
Рассмотрим процесс остывания (4-6) в течение времени t . Уравнение баланса энергии для газа находящегося в баллоне может быть записано в виде:
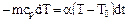 , (3)
, (3)
где сР- удельная теплоемкость газа, a - коэффициент теплоотдачи, m - переменная масса газа в баллоне:
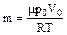 ,
,
где Т - температура газа в момент времени t, μ – молярная масса воздуха. Подставив массу m в левую часть выражения (3) и преобразуя выражение, получим:
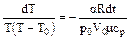 (4)
(4)
Используем, что 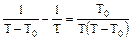 , тогда выражение (4) примет вид:
, тогда выражение (4) примет вид:
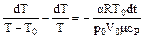 (5)
(5)
Интегрируя (5),получим уравнение:
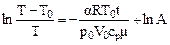
Константу интегрирования А найдем из условия, что при t = 0
Т1 = Т0 - DТ1 Окончательное соотношение имеет вид:
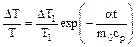 , (6)
, (6)
где 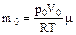 - масса газа, находящегося в начальном состоянии.
- масса газа, находящегося в начальном состоянии.
Температура газа Т тем больше, чем больше время выдержки t. После того, как в момент времени t клапан закрывается, нагрев газа в баллоне продолжается изохорно. Давление газа в конце концов достигает величины р = р0 + Δр.
Из условия изохорности следует:
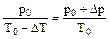
После преобразований имеем:
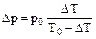 (7)
(7)
Уравнение адиабатического процесса (3 - 4) можно записать в виде:

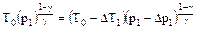 ,
,
после преобразований имеем выражение:

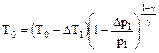 =>
=> 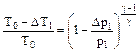 ,
,
учитывая малость Δр1 , получим: 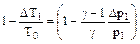 , и наконец:
, и наконец:
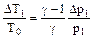 (8)
(8)
Подставляем соотношения (7, 8) в (6) и, учитывая, что Т1 = Т0 - DТ1, получаем формулу:
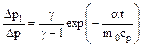 (9)
(9)
Это соотношение учитывает, как теплообмен, так и уход газа из баллона в процессе нагрева. Соотношение (10) позволяет найти g по измеренным при разных величинах t значениям Δр1 и Δр. График зависимости 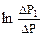 от t является линейной функцией. Если экстраполировать этот график до t = 0, то он будет отсекать на оси ординат отрезок:
от t является линейной функцией. Если экстраполировать этот график до t = 0, то он будет отсекать на оси ординат отрезок:
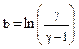 (10)
(10)
Из последнего выражения легко находится отношение теплоемкостей или показатель адиабаты:
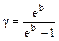 (11)
(11)