Основы молекулярно – кинетической теории газов
Термодинамическая система представляет собой совокупность большого числа частиц. В идеальном газе эти частицы движутся хаотично с различными скоростями, т.е. представляют собой статистическую систему. Для описания состояния статистической системы используются усредненные величины: среднее число столкновений, средняя длина свободного пробега, средняя арифметическая и средняя квадратичная скорости, наиболее вероятная скорость; функции распределения частиц по параметрам и др.
Основное уравнение МКТ имеет вид:
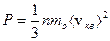 , (3.1)
, (3.1)
где P – давление системой на поверхность сосуда; n – концентрация молекул, т.е. число частиц в единице объема 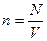 ;
; 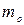 - масса одной молекулы;
- масса одной молекулы; 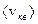 - средняя квадратичная скорость молекул;
- средняя квадратичная скорость молекул;
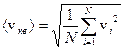 (3.2)
(3.2)
где 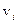 - скорость i –той молекулы; N – общее число молекул в системе.
- скорость i –той молекулы; N – общее число молекул в системе.
Если учесть, что кинетическая энергия движения одной молекулы 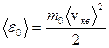 то можно записать:
то можно записать:
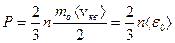 (3.3)
(3.3)
где 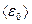 - средняя кинетическая энергия поступательного движения молекул.
- средняя кинетическая энергия поступательного движения молекул.
Используя уравнение состояния в виде 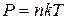 , можно получить:
, можно получить:
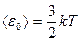 (3.4)
(3.4)
Из (3.4) видно, что температура T является мерой средней кинетической энергии движения молекул в термодинамической системе. Сравнение выражений для энергии позволяет получить выражение для 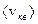 ;
;
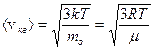 (3.5)
(3.5)
где: 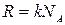 ;
; 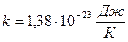 - постоянная Больцмана;
- постоянная Больцмана; 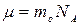 - молярная масса газа.
- молярная масса газа.
Т.к скорости молекул различны, то распределение молекул по скоростям при различных температурах 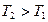 имеет вид, изображенный на рис. (3.1). Наибольшее число молекул обладают наиболее вероятной скоростью:
имеет вид, изображенный на рис. (3.1). Наибольшее число молекул обладают наиболее вероятной скоростью:
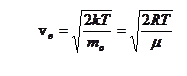
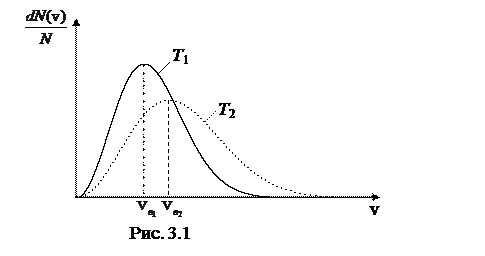 (3.6)
(3.6)
|
Такое распределение описывается функцией Максвелла (рис. 3.2):
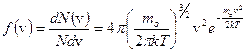 . (3.7)
. (3.7)
Таким образом, состояние газа характеризуется скоростями:
- наиболее вероятной 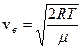 ;
;
- средней 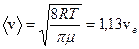 ;
;
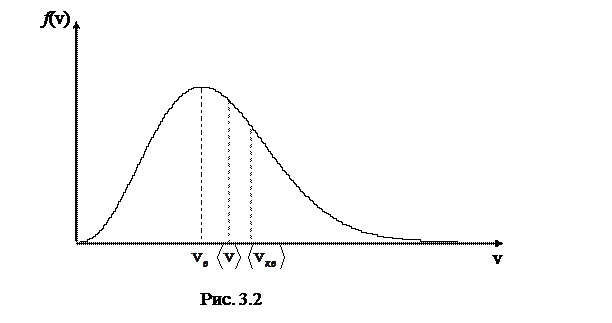 - средней квадратичной
- средней квадратичной 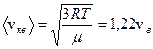 .
.
Для всей совокупности молекул также характерна средняя арифметическая скорость
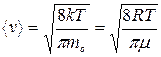 (3.8)
(3.8)
Функции распределения (3.7) молекул по скоростям соответствует распределение молекул по энергиям ε
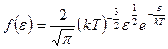 . (3.9)
. (3.9)
Молекулы любого газа находятся в поле тяготения Земли. Тяготение и тепловое движение молекул приводят газ в некоторое стационарное состояние, при котором давление газа с высотой убывает:
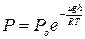 , (3.10)
, (3.10)
где: P – давление на высоте h; 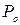 - давление на уровне моря (т.е. на поверхности);
- давление на уровне моря (т.е. на поверхности); 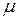 - молярная масса газа.
- молярная масса газа.
Это выражение называется барометрической формулой. Связь давления с концентрацией молекул 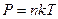 позволяет записать:
позволяет записать:
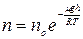 (3.11)
(3.11)
Так как 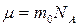 и
и 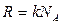 , то
, то 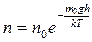 или
или 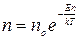 , (3.11а)
, (3.11а)
где 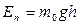 - потенциальная энергия молекулы в поле тяготения.
- потенциальная энергия молекулы в поле тяготения.
Это соотношение называется распределением Больцмана, из которого следует, что при постоянной температуре плотность частиц больше там, где меньше их потенциальная энергия.
Явления переноса в термодинамических
