Порядок выполнения работы. 1. Ознакомиться с машиной Атвуда

1. Ознакомиться с машиной Атвуда.

2. Скомпенсировать силу трения в блоке, добавляя к правому грузу, движущемуся вниз, небольшой грузик (кусочек пластилина или проволоки). При компенсации силы трения система тел, выведенная из равновесия легким толчком, движется равномерно. Равномерность движения определяется визуально. (Во время дальнейшей работы нужно следить за тем, чтобы положение грузов “левое” и “правое” не менялось.)

3. Положить на левый и правый грузы перегрузки известной

массы m₁ и m₂, где правый перегрузок m₂ > m₁.

4. Измерить время t₁ движения системы. Опыт повторить пять раз.

5. Оба перегрузка m₁ и m₂ положить на правый груз. Измерить время движения t₂ также пять раз.

Результаты всех измерений записать в табл. I.

Таблица I

Номер опыта	Время t1i, с	(t1i - <t1>)2	Время t2i, c	(t2i - <t2>)2	Масса перегрузка
m1, г	m2, г
t(a, n)	<t1>, c	å(t1i - <t1>)2	<t2>, c	å(t2i - <t2>)2	Dm1, г	Dm2, г

6. По формуле (6) вычислить отношение сил, обозначенное через X₁, по формуле (8) – отношения ускорений X₂, подставляя средние значения времени <t₁> и <t₂>.

7. Вычислить абсолютную погрешность измерения времени t₁:

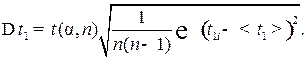Здесь t(a, n) – коэффициент Стьюдента для доверительной вероятности a = 0,95 и числа измерений n = 5. Аналогично вычисляется абсолютная погрешность измерения времени Dt₂.

8. Вычислить относительную погрешность измерения отношения ускорений

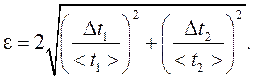9. Вычислить абсолютную погрешность измерения отношения ускорений:

DX₂ = eX₂.

10. Вычислить абсолютную погрешность измерения отношения сил:

Здесь Δm – абсолютная погрешность измерения массы перегрузков.

11. Записать результаты вычислений в виде

X₁ = …± … , X₂ = …± … .

12. Сравнить полученные значения X₁ и X₂, которые должны совпадать в пределах ошибок:

Выполнение этого неравенства является критерием выполнимости следствия (2) второго закона Ньютона. Сделать вывод.

ЗАДАНИЕ № 2

Цель работы: на машине Атвуда проверить следствие (3) второго закона Ньютона при постоянной силе. По результатам измерений определить отношение масс и отношение ускорений. Полученные результаты сравнить. Следствие (3) проверяется при движении системы тел под действием силы тяжести.

Если на правый груз C₂, движущийся вниз, поместить перегрузок массой m₀, то на систему тел будет действовать сила, равная силе тяжести m₀g перегрузка. Движение будет равноускоренным с ускорением а₁.

Общая масса системы

m₁ = 2M +m₀, (9)

где M– масса груза.

Если на левый и правый грузы добавить перегрузки одинаковой массы m₃, то результирующая сила не изменится. Однако, система будет двигаться с другим ускорением а₂, поскольку изменилась движущая масса. Общая масса системы тел увеличилась на 2m₃ и стала равной

m₂ = 2M + m₀ +2m₃. (10)

Найдем отношение масс:

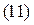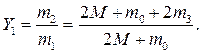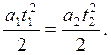В обоих случаях система тел проходит равноускоренно одинаковый путь, следовательно

Из равенства (12) найдем отношение ускорений: