Собственная звукоизоляция. Нормальное и наклонное падение звука. Закон «масс»

Одним из самых эффективных средств снижения воздушного шума является устройство на пути его распространения звукоизолирующих преград в виде стен, перегородок, перекрытий, специальных звукоизолирующих кожухов, экранов и т.п.

Звукоизоляция – способность ограждающей конструкцией снижать звуковую энергию при передаче её через ограждающую конструкцию.

Собственная звукоизоляция (ЗИ) ограждающих конструкций без учета косвенной передачи звука равна

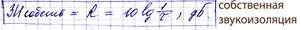
Где, τ- коэфицент звукопроницаемости или прохождения звука

τ= Е_пр/Е_пад =W_пр/W_пад= р²_пр/р²_пад

ЗИ_собств = ЗИ_факт+ΔR_косв

ЗИ_факт = ЗИ_собств-ΔR_косв

W- звуковая мощность

Е – энергия

Р – давление звуковой волны

пад –падающих звуковых волн

пр–прошедшая через преграду

Сущность ЗИ ограждения состоит в том, что большая часть падающей звуковой энергии отражается, какая-то часть поглощается и лишь незначительная часть (0,001- 0,00001 и менее) проходит через ограждение, при этом собственная звукоизоляция составляет 30дБ-50дБ

Экспериментально или при натурных измерениях ЗИ определяется:

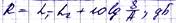
L₁ – уровень звукового давления в помещении высокого уровня ПВУ, дБ

L₂ – уровень звукового давления в помещении низкого уровня ПНУ, дБ

10lgS/A – поправка на звукопоглощение в ПНУ

S – площадь ограждения

А- эквивалентная площадь звукопоглощения в ПНУ

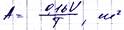
V – объем ПНУ

В натурных условиях – фактическая звукоизоляция.

В лабораторных условиях – собственная звукоизоляция.

Для определения численного значения собственной звукоизоляции необходимо знать механизм прохождения звука через ограждение.

Первые теоретические исследования прохождения звука через ограждение были сделаны еще в 19в Англии физиком Релейем.

Он рассмотрел задачу прохождения звука через преграду неограниченной протяженности при перпендикулярном падении на неё простых звуковых волн и сделал вывод, что звук проходит через ограждение в результате нормальных поршневых колебаний.

Это зависимость ЗИ выражает так называемый закон массы. Из формулы видно, что при каждом удвоении массы, толщины или частоты звукоизоляция увеличивается на 6 дБ.

В дальнейшем Шох показал, что в случае. Когда плоские звуковые волны падают на ограждение под углом Ɵ(наклонное падение), звукоизоляция равна:

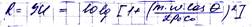
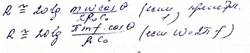
Задачу прохождения звука через тонкую бесконечную пластину при разных углах падения плоских звуковых волн решил немецкий физик Л. Кремер (1942 г.)

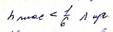
Кремер установил, что основное влияние на передачу звука через тонкую пластину оказывают изгибные волны. В основе теории Кремера заложен эффект волнового совпадения.