Магнитное поле. Закон Био-Савара-Лапласа
Движущийся заряд q, создает вокруг себя магнитное поле, индукция которого
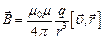 ,
,
где 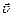 – скорость электрона,
– скорость электрона, 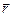 – расстояние от электрона до данной точки поля, μ – относительная магнитная проницаемость среды, μ0 = 4π·10-7 Гн/м – магнитная постоянная.
– расстояние от электрона до данной точки поля, μ – относительная магнитная проницаемость среды, μ0 = 4π·10-7 Гн/м – магнитная постоянная.
По закону Био-Савара-Лапласа элемент контура dl, по которому течет ток I, создает вокруг себя магнитное поле, индукция которого в некоторой точке K
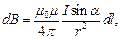
где 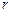 – расстояние от точки K до элемента тока dl, α – угол между радиус-вектором
– расстояние от точки K до элемента тока dl, α – угол между радиус-вектором 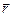 и элементом тока dl.
и элементом тока dl.
Направление вектора  можно найти по правилу Максвелла (буравчика): если ввинчивать буравчик с правой резьбой по направлению тока в элементе проводника, то направление движения рукоятки буравчика укажет направление вектора магнитной индукции
можно найти по правилу Максвелла (буравчика): если ввинчивать буравчик с правой резьбой по направлению тока в элементе проводника, то направление движения рукоятки буравчика укажет направление вектора магнитной индукции  .
.
Применяя закон Био-Савара-Лапласа к контурам различного вида, получим:
· в центре кругового витка радиуса R с током силой I магнитная индукция 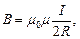
·  магнитная индукция на оси кругового тока
магнитная индукция на оси кругового тока 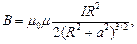 где a – расстояние от точки, в которой ищется B до плоскости кругового тока,
где a – расстояние от точки, в которой ищется B до плоскости кругового тока,
· поле, созданное бесконечно длинным проводником с током, на расстоянии r от проводника 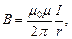
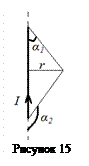
· поле, созданное проводником конечной длины, на расстоянии r от проводника (рис. 15) 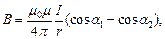
· поле внутри тороида или бесконечно длинного соленоида 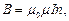 n – число витков на единицу длины соленоида (тороида)
n – число витков на единицу длины соленоида (тороида)
Вектор магнитной индукции связан с напряженностью магнитного поля соотношением
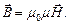
Объемная плотность энергии магнитного поля:
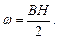
401. Два параллельных бесконечно длинных провода, по которым текут токи силы I = 60 А в одном направлении, расположены на расстоянии d = 10 см друг от друга. Определите магнитную индукцию B в точке, находящейся на расстоянии r1 = 5 см от одного и на расстоянии r2 = 12 см от другого.
402. Два параллельных бесконечно длинных провода, по которым текут токи силы I = 15 А в противоположных направлениях, расположены на расстоянии d = 5 см друг от друга. Определите магнитную индукцию B в точке, находящейся на расстоянии r = 5 см от каждого проводника.
403. Ток I = 60 А идет по длинному проводнику, согнутому под прямым углом. Найти индукцию магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии d = 20 см.
404. По тонкому проводу, изогнутому в виде прямоугольника со сторонами а = 80 см и b = 60 см, течет ток силы I = 25 A. Определите напряженность магнитного поля H в точке пересечения диагоналей прямоугольника.
405. По тонкому проволочному кольцу течет ток. Как нужно изменить силу тока в проводнике, что, придав проводнику форму квадрата магнитная индукция в центре контура не изменилась?
| 406. Найти величину тока в бесконечно длинном проводнике, который имеет квадратный изгиб, изображенный на рис. 16 со стороной a = 15 см, если модуль магнитной индукции магнитного поля в точке А, равен В = 50 мкТл. 407. Индукция магнитного поля в центре | 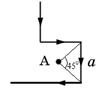 Рисунок 16 Рисунок 16 |
кругового витка радиусом R = 11 см равна B = 80 мкТл. Найти индукцию магнитного поля на оси витка на расстоянии d = 10 см от его плоскости.
| 408. Определите магнитную индукцию B в точке A (см. рис. 17), если по проводнику течет ток I = 10 A, а сторона треугольника a = 5 см. 409. Маленький шарик с зарядом q = 5∙10-7 Кл, подвешенный на невесомой нерастяжимой нити длины L = 1 м, движется равномерно по окружности в горизонтальной плоскости так, что | 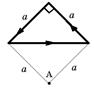 Рисунок 17 Рисунок 17 |
нить все время образует с вертикалью угол α = 60o. Определите напряженность магнитного поля в центре окружности, рассматривая движение шарика как круговой ток.
410. Определить магнитную индукцию поля, создаваемого током I = 30 A, текущим по проводу, согнутому в виде правильного треугольника со стороной a = 30 см, в вершине правильного тетраэдра для которого этот треугольник служит основанием.
