Статистическое описание систем с большим числом степеней свободы
Квантовая теория и статистическая физика
(Часть II)
Статистическая физика
Конспект лекций для студентов ЭКТ-2
Г.
Оглавление
§1. Статистическое описание систем с большим числом степеней свободы.. 3
§2. Метод статистической физики(элементы теории вероятностей) 3
§3. Микро- и макро- параметры системы. 4
§4. Свойство эргодичности системы. 5
§5. Два способа усреднения в статистической физике. 5
§6. Понятие ансамбля систем.. 6
§7. Эргодическая гипотеза. 6
§8. Равновесное состояние системы.. 7
§9. Время релаксации. 7
§10. Квазизамкнутость и статистическая независимость подсистем.. 7
§11. Принцип равновероятности микросостояний. 8
§12. Статистический вес макросостояния. 8
§13. Статистическая энтропия. 8
§14. Теорема Лиувилля. 8
§15. Микроканоническое распределение Гиббса. 9
§16. Каноническое распределение Гиббса. 10
§17. Принцип возрастания энтропии. 13
§18*. Статистическая сумма и её свойства. 13
§19*. Функция распределения вероятностей по энергии 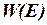 и распределение Гаусса. 15
и распределение Гаусса. 15
§20. Квазиклассическое приближение в статистической физике. 17
§21*. Распределение Максвелла как следствие канонического распределения Гиббса. 19
§22. Использование распределения Максвелла для расчёта средних: 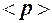 ,
, 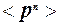 ,
, 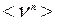 ,
, 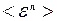 ............. 21
............. 21
§23. Большое каноническое распределение. 22
§24. Термодинамический потенциал Гиббса. 23
§25. Распределение Ферми-Дирака. 24
§26. Распределение Бозе-Эйнштейна. 25
§27. Ферми и Бозе газы элементарных частиц. 26
§28. Расчёт импульса Ферми для электронного газа при 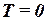 ........... 28
........... 28
§29. Расчёт энергии электронного газа при 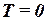 ........... 29
........... 29
§30*. Уравнение состояния идеального электронного газа при 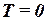 . Критерий идеальности электронного газа. 30
. Критерий идеальности электронного газа. 30
§31*. Числовые оценки параметров 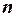 ,
, 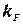 ,
, 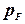 ,
, 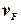 ,
, 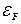 и
и 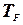 ..... 31
..... 31
Экзаменационные вопросы по курсу “Статистическая физика”. 33
Экзаменационные задачи по курсу “Статистическая физика”. 34
Экзаменационные вопросы и задачи по курсу “Статистическая физика” (минимум) 36
Решение задач по курсу “Статистическая физика”. 37
Статистическое описание систем с большим числом степеней свободы
Статистическая физика изучает системы с большим числом степеней свободы. Наличие большого число степеней свободы вносит некоторые особенности в описание таких систем. Например, в 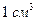 воздуха содержится ~ 2.7,·1019 частиц (число Лошмидта), но у каждой материальной точки (частицы) имеется 3 степени свободы, поэтому у этой системы огромное число степеней свободы.
воздуха содержится ~ 2.7,·1019 частиц (число Лошмидта), но у каждой материальной точки (частицы) имеется 3 степени свободы, поэтому у этой системы огромное число степеней свободы.
В классической механике возможно описывать такие системы (через формализм Гамильтона) - 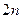 динамических переменных
динамических переменных 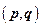 , где
, где 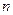 - число степеней свободы. Описание системы сводится к решению уравнений:
- число степеней свободы. Описание системы сводится к решению уравнений:
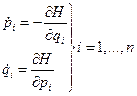
Чтобы решить данную систему, необходимо задать 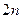 начальных условий. Задаем начальные условия и решаем систему. Но здесь сложные технические трудности(долгий счёт на ЭВМ). Но имеются ещё и качественные особенности этих систем, которые не охватываются этими уравнениями, т.е. детерминированный подход здесь не используют.
начальных условий. Задаем начальные условия и решаем систему. Но здесь сложные технические трудности(долгий счёт на ЭВМ). Но имеются ещё и качественные особенности этих систем, которые не охватываются этими уравнениями, т.е. детерминированный подход здесь не используют.
Статистическая физика рассматривает переход от малого числа степеней свободы к большому. 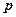 и
и 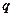 - это динамические переменные. Фазовое пространство – это
- это динамические переменные. Фазовое пространство – это 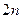 мерное пространство, декартовыми осями которого являются переменные
мерное пространство, декартовыми осями которого являются переменные 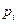 и
и 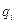 . Тогда состояние системы (которое задаётся динамическими переменными) в фазовом пространстве задаётся фазовой точкой. Движение системы в реальном пространстве задаётся движением фазовой точки в фазовом пространстве, т.е. устанавливается соответствие между фазовым и реальным пространствами.
. Тогда состояние системы (которое задаётся динамическими переменными) в фазовом пространстве задаётся фазовой точкой. Движение системы в реальном пространстве задаётся движением фазовой точки в фазовом пространстве, т.е. устанавливается соответствие между фазовым и реальным пространствами.
