В термодинамической системе вероятнее всего будут развиваться такие процессы, которые сопровождаются возрастанием термодинамической вероятности

Особенности термодинамической вероятности.

1. Термодинамическая вероятность W – однозначная функция состояния системы, т.е. она является полным дифференциалом.

2. В равновесном состоянии термодинамическая вероятность W максимальна.

3. Если система не находится в равновесии, то ее наиболее вероятным изменением термодинамической вероятности W является ее возрастание.

4. Термодинамическая вероятность W – величина мультипликативная.

Термодинамическая вероятность W системы, состоящей из невзаимодействующих частей, равна произведению вероятностей состояния этих частей (теорема умножения вероятностей).

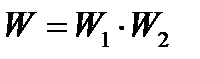Подсчитаем число микросостояний, посредством которых может быть реализовано макросостояние системы, состоящей из двух независимых подсистем, находящихся в макросостояниях с вероятностями W₁ и W₂. Очевидно, взяв с одним из W₁ микросостояний из первой подсистемы любое из W₂ микросостояний второй подсистемы, получим одно из микросостояний всей системы. Число всех возможных пар равно:

36. Идеальная тепловая машина. Цикл Карно. Теорема Карно.

Идеальная тепловая машина.

Тепловая машина-это устройство, преобразующее тепловую энергию и механическую машину ( тепловой двигатель) или механическую работу в тепло (холодильник).

Идеальная тепловая машина- это машина, в которой произведенная работа и разница между количеством подведенного и отведенного тепла равны.

Одним из важных применений термодинамики для практики, является теория тепловых машин.

Тепловые двигатели.

Тепловой двигатель– это устройство, преобразующее внутреннюю энергию одних тел (топлива) в механическую работу других тел.

Тепловой двигатель состоит из:

1.Нагревателя.

2.Рабочего тела.

3.Охладителя.

В качестве рабочего тела в тепловых двигателях используется газ.

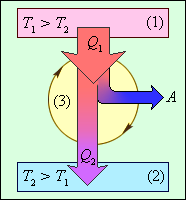
1 – нагреватель;

2 – охладитель;

3 – рабочее тело, совершающее круговой процесс.

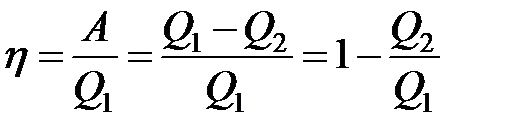Q₁ > 0, A > 0, Q₂ < 0; T₁ > T₂.

КПД теплового двигателя:

где Q₁ – количество теплоты подводимое от нагревателя к рабочему телу; Q₂ – количество теплоты отданное рабочим телом охладителю.

Работа тепловой машины происходит по схеме.

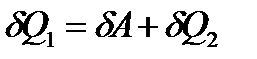От нагревателя 1 с температурой Т₁ – теплота передается рабочему телу 3 и частично преобразуется последним в работу; частично же теплота от рабочего тела передается охладителю 2 с температурой Т₂, а рабочее тело возвращается в исходное состояние.

В соответствии с ПНТ необходимо, чтобы выполнялось равенство:

Работа за один цикл измеряется площадью, охваченной кривой, описывающий процесс.

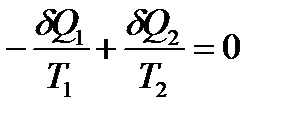В соответствии со ВНТ необходимо, чтобы изменение энтропии всей системы ΔS=0, т.е. для обратимого процесса:

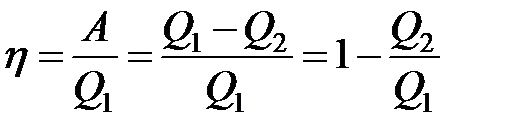
КПД тепловой машины:

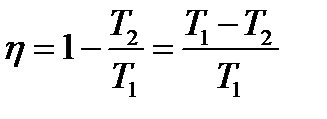
Для идеальной тепловой машины КПД определяется выражением:

КПД идеальной машины определяется только температурами нагревателя и охладителя. Мощность тепловой машины определяется произведением работы, совершаемой за один цикл, на число циклов, происходящих за 1 с.

Цикл Карно.

В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат. Этот круговой процесс сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно.

Цикл Карно имеет наибольший КПД среди всех циклов, работающих между данными температурами T₁ и T₂.

Цикл Карно – это цикл, состоящий из двух изотерм и двух адиабат.

Тепловой двигатель, работающий по циклу Карно, называется идеальным.

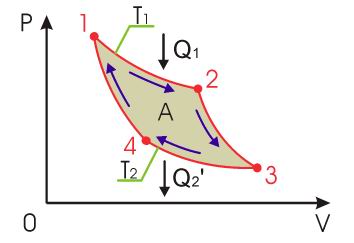
На участке 1–2 газ изотермически расширяется, совершая работу A₁₂, при этом к газу подводится количество теплоты Q₁. Далее на адиабатическом участке 2–3 газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A₂₃ > 0. Температура газа при этом падает до значения T₂. На участке 3–4 происходит процесс изотермического сжатия.

Газ отдает тепло Q₂ < 0. На участке 4-1 газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T₁. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:

A = A₁₂ + A₂₃ + A₃₄ + A₄₁.

На p-V- диаграмме эта работа равна площади цикла.

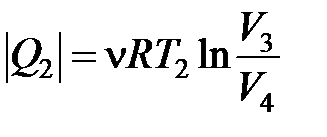
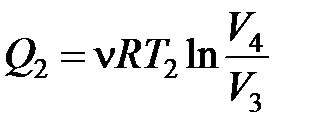
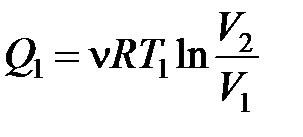
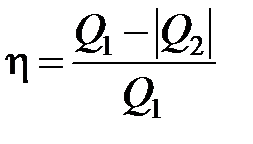Рассчитаем КПД такого цикла:

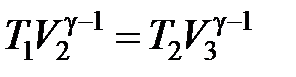
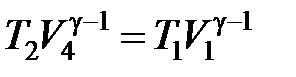
Воспользуемся уравнением Пуассона для участков 2-3 и 4-1:

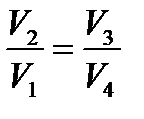
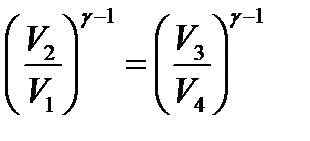Поменяем в уравнении (5) левую и правую часть местами и поделим почленно на него уравнение (4):

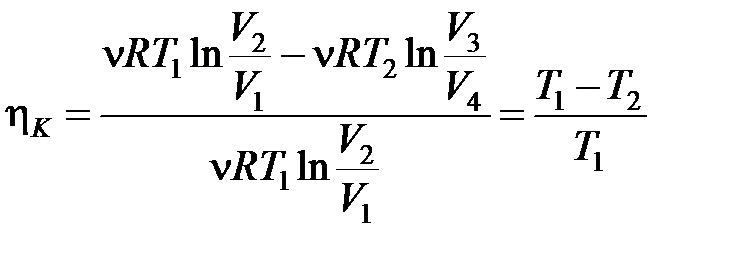Подставляя (2), (3) и (6) в (1), получим:

КПД цикла Карно:

Теоремы Карно.

Первая теорема Карно:КПД идеального цикла Карно не зависит от рада рабочего тела.

Вторая теорема Карно:КПД идеальной обратимой тепловой машины не может быть меньше КПД реальной необратимой машины.

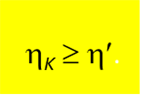
37.Энтропия. Неравенство Клаузиуса. Приращение энтропии в изопроцессах.

Энтропия.

Л. Больцман доказал, что функция состояния термодинамической системы, называемой энтропией S, связана с термодинамической вероятностью W соотношением:

S = klnW + C

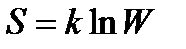где C = const, для удобства берем C = 0.

Формула Больцмана:

где k – постоянная Больцмана.

Энтропия, а значит, и второй закон термодинамики имеет вероятностный характер. Она связана с процессом перехода системы из менее вероятных в более вероятные состояния. Такой процесс происходит за счет хаотического теплового движения. Поэтому энтропия является мерой хаоса в системе.

Энтропия– СФВ, характеризующая макросостояние термодинамической системы и числено равная постоянной Больцмана, умноженной на логарифм термодинамической вероятности этого состояния.

Формула Больцмана имеет фундаментальное значение. Она соединяет термодинамику со статистической физикой и позволяет рассчитать энтропию статистическими методами.

Энтропия непосредственно связана с термодинамической вероятностью и ее свойства определяются свойствами термодинамической вероятности.

Свойства энтропии:

1. Энтропия – однозначная функция состояния системы.

2. В равновесном состоянии энтропия максимальна.

3. Если система не находится в равновесии, то наиболее вероятным изменением энтропии является ее возрастание.

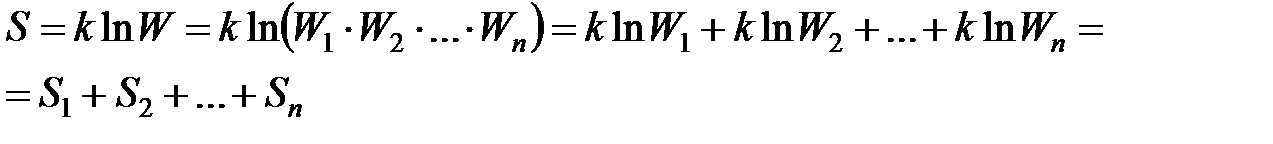4. Энтропия – величина аддитивная: энтропия системы, состоящей из невзаимодействующих частей, равна сумме энтропий этих частей:

5. Энтропия – величина статистическая.

Найдем связь между изменением энтропии и количеством теплоты сообщённого ей:

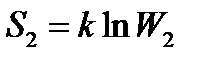
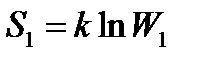Рассмотрим равновесное изотермическое расширение ИГ от объема V₁ до V₂.

В процессе расширения газа его энтропия получает приращение ΔS:

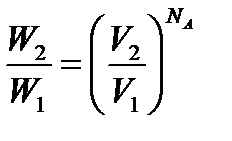Так как процесс изотермический, то в данном случае изменяется только число пространственных ячеек (объем системы увеличивается). При изотермическом расширении выполняется соотношение:

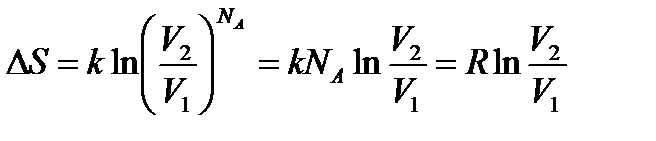Подставим полученное соотношение в формулу изменения энтропии, получим:

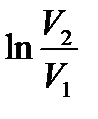
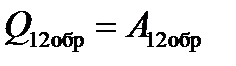
Найдем воспользовавшись ПНТ для изотермического процесса :

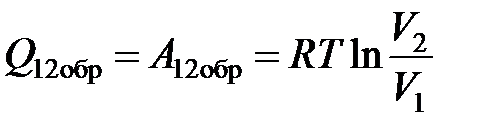Работа, совершаемая газом при обратимом изотермическом расширении (ν=1 моль), равна:

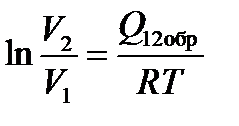
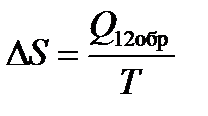
Откуда

Подставив это выражение в , получим равенство Клаузиуса:

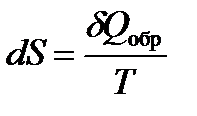
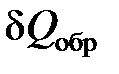Если процесс связан с малым обратимым изменением состояния, то

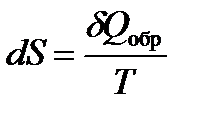Величина, числено равная отношению количества тепла , полученной системой в изотермическом процессе, к температуре процесса Т, называется приведенным количеством теплоты (приведенной теплотой).

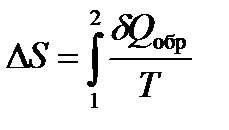Соотношение справедливо для любого обратимого процесса.

Конечное приращение энтропии при произвольном обратимом процессе равно: