Разветвленные цепи. Правила Кирхгофа
Расчет разветвленных цепей значительно упрощается, если пользоваться правилами, сформулированным Кирхгофом. Этих правил два. Первое из них относится к узлам цепи. Узлом называется точка, в которой сходится более чем два проводника. Ток, текущий к узлу, считается имеющим один знак, текущий от угла – имеющим другой знак.
Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:
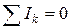 . (15.5)
. (15.5)
Справедливость этого утверждения вытекает из следующих соображений. Если бы алгебраическая сумма токов была отлична от нуля, в узле происходило бы накапливание или уменьшение заряда, что в свою очередь приводило бы к изменению потенциала узла и изменению текущих в цепи токов. Таким образом, чтобы токи в цепи были постоянными, должно выполняться условие (15.5).
Уравнение (15.5) можно записать для каждого из N узлов цепи. Однако независимыми являются только N-1 уравнение, N-е будет следствием из них.
Выделим мысленно в разветвленной цепи произвольный замкнутый контур (1-2-3-4-1). Зададимся направлением обхода (например, по часовой стрелке) и применим к каждому из неразветвленных участков контура закон Ома:

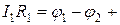 e1,
e1,

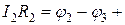 e2,
e2,

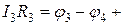 e3,
e3,

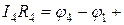 e4.
e4.
При сложении этих выражений потенциалы сокращаются и получается уравнение
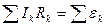 , (15.6)
, (15.6)
которое выражает второе правило Кирхгофа.

Рис. 15.3.
Уравнение (15.6) может быть составлено для всех замкнутых контуров, которые можно мысленно выделить в данной разветвленной цепи. Но независимыми будут только уравнения для тех контуров, которые нельзя получить наложением других контуров друг на друга.
С помощью законов Кирхгофа можно моделировать расчет замкнутых гидравлических, аэродинамических и тепловых контуров.
Например, при расчете систем охлаждения автомобиля масляный насос, являющийся источником давления считается электродвижущей силой, секундный расход масла считается силой тока, а гидравлическое сопротивление системы считается активным сопротивлением цепи. Для новых переменных записываются аналоги законов Кирхгофа и производится гидравлический расчет масляного контура.
ГЛАВА 16. МАГНИТНОЕ ПОЛЕ ТОКОВ
Закон Ампера
Французский физик А.Ампер в 1820г подробно исследовал действие магнитного поля на проводники с током и пришел к выводу, что сила 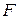 , действующая на прямолинейный проводник с током, помещенный в однородное магнитное поле, прямо пропорциональна силе тока
, действующая на прямолинейный проводник с током, помещенный в однородное магнитное поле, прямо пропорциональна силе тока 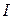 в проводнике, его длине
в проводнике, его длине 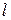 , магнитной индукции В и синусу угла a между направлением тока в проводнике и вектором
, магнитной индукции В и синусу угла a между направлением тока в проводнике и вектором 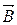 :
:
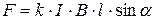 .
.
Закон Ампера легко обобщить на случай неоднородного магнитного поля и проводника произвольной формы. Магнитное поле называется однородным, если векторы индукции во всех точках этого поля одинаковы, т.е. численно равны и имеют одинаковые направления.
Бесконечно малый элемент 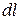 проводника любой формы можно считать прямолинейным, а магнитное поле в области, занятой элементом
проводника любой формы можно считать прямолинейным, а магнитное поле в области, занятой элементом 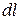 можно считать однородным.
можно считать однородным.
Поэтому в общем случае закон Ампера имеет вид:
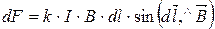 , (16.1)
, (16.1)
где 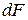 - сила, действующая на элемент проводника длиной
- сила, действующая на элемент проводника длиной 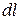 , а угол a заменен углом между векторами
, а угол a заменен углом между векторами 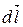 (проведенным в направлении тока
(проведенным в направлении тока 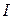 ) и
) и 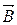 . Коэффициент пропорциональности зависит от выбора единиц измерения
. Коэффициент пропорциональности зависит от выбора единиц измерения 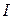 , В,
, В, 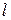 и
и 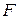 . При измерении всех этих величин в единицах одной и той же системы единиц
. При измерении всех этих величин в единицах одной и той же системы единиц 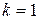 (исключением является только система единиц Гаусса). Поэтому в дальнейшем коэффициент
(исключением является только система единиц Гаусса). Поэтому в дальнейшем коэффициент 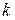 в законе Ампера мы будем опускать.
в законе Ампера мы будем опускать.
Закон Апмпера позволяет определить численное значение магнитной индукции В. Предположим, что элемент проводника 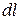 с током
с током 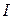 перпендикулярен к направлению магнитного поля
перпендикулярен к направлению магнитного поля 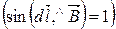 , тогда закон Ампера можно записать в виде:
, тогда закон Ампера можно записать в виде:
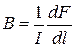 .
.
Из этой формулы следует, что магнитная индукция 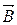 численно равна силе, действующей со стороны поля на единицу длины проводника, по которому течет электрический ток единичной силы и который расположен ^ к направлению магнитного поля. Таким образом магнитная индукция является силовой характеристикой магнитного поля подобно тому, как напряженность
численно равна силе, действующей со стороны поля на единицу длины проводника, по которому течет электрический ток единичной силы и который расположен ^ к направлению магнитного поля. Таким образом магнитная индукция является силовой характеристикой магнитного поля подобно тому, как напряженность 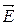 является силовой характеристикой электростатического поля.
является силовой характеристикой электростатического поля.
Закон Ампера, записанный в форме (16.1), не указывает направление силы 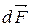 . Как показали опыты, направление силы
. Как показали опыты, направление силы 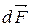 можно найти по правилу левой руки. Однако лучше пользоваться более универсальным правилом: вектор
можно найти по правилу левой руки. Однако лучше пользоваться более универсальным правилом: вектор 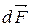 направлен перпендикулярно к плоскости, образованной векторами
направлен перпендикулярно к плоскости, образованной векторами 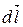 и
и 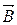 таким образом, чтобы из конца вектора
таким образом, чтобы из конца вектора 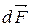 вращение от вектора
вращение от вектора 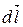 к вектору
к вектору 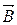 по кратчайшему пути происходило против часовой стрелки. Иными словами вектор
по кратчайшему пути происходило против часовой стрелки. Иными словами вектор 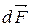 совпадает по направлению с векторным произведением
совпадает по направлению с векторным произведением  . Из математики известно, что модуль векторного произведения равен произведению модулей векторов на синус угла между ними:
. Из математики известно, что модуль векторного произведения равен произведению модулей векторов на синус угла между ними:
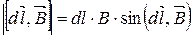 .
.
Поэтому можно записать закон Ампера в векторной форме следующим образом:
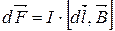 .
.
