Вектор магнитной индукции

Мы собираемся изучать магнетики - вещества в магнитном поле, создавае­мого постоянными токами.

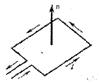
Еще из опытов Эрстеда известно, что магнитное поле тока ориентирующе действует на магнитную стрелку. Маг­нитная стрелка ориентируется перпендикулярно к направлению тока, северным концом по известному правилу правого винта (буравчика). При исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), размеры которого малы по сравнению с расстоянием до токов, образующих исследуемые магнитные поля. 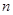За направление магнитного поля в данной точке принимается направление нормали к рамке, определяемое правилом правого винта, оно совпадает с направлением силы, действующей на северный полюс магнитной стрелки. Рамку с током используют и для количественного описания магнитного поля. Рамка с током в магнитном поле ориентируется под действием магнитных сил поля вполне определенном направлении. Если пропустить по рамке ток I, и создать механический момент, например, за счет сил упругости, как в измерительных приборах, то можно убедиться, что M_MAX ~ I (М_MAX - максимальный механический момент сил) М_MAX ~ S ( площадь рамки-контура).

Cледовательно, при любых токах и площадях контура M_MAX ~ IS , то есть M_MAX /IS=В – есть величина постоянная для данного поля в данной точке. В другой точке поля эта величина так е постоянная, но другая. Следовательно, эта величина отношения является характеристикой магнитного поля в данной точке. Ее называют вектором магнитной индукции ( 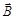) магнитного поля в данной точке. Единица измерения магнитной индукции Тесла (Тл). 1 Тл - магнитная индукция однородного магнитного поля, которая в рамке площадью 1 м² током 1 А создает механический момент 1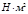

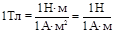(F=BIl)

p= I S - называется магнитным моментом рамки.

Для удобства изображения магнитных полей, еще Фарадей ввел понятие силовых линий (линий магнитной индукции).

Численная величина вектора магнитной индукции определяется густотой силовых линий, а направление - направлением касательной к силовой линии в данной точке поля.

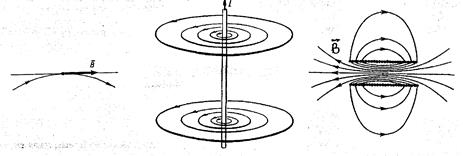
Линии магнитной индукции всегда замкнуты (вихревые) и всегда охватывают проводник с током. В отличии от линий напряженности электрического поля, которые начинаются на по­ложительном заряде и заканчиваются на отрицательном (см. рис. а).

Магнитное поле, проходящее через площадь S, характеризуется скалярной величиной Ф

называемой потоком вектора магнитной индукции (магнитным потоком): Ф_в = 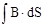(1)

Для однородного поля плоской поверхности, расположенной перпендикулярно вектору 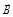: Ф_в=В S. Измеряется в Веберах. 1 Вебер (Вб) - магнитный поток, пронизывающий поверх­ность площадью 1 м² перпендикулярную однородному полю с индукцией 1 Тл (1 Вб = 1 Тл м²).

Мы рассматривали токи, создающие макроскопические магнитные поля. Однако, со­гласно гипотезе Ампера, в любом веществе существуют микроскопические токи, обусловлен­ные движением электронов в атомах и молекулах. Эти микроскопические токи создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков. Например, если вбли­зи какого-то тела поместить проводник с током (макроток), то под действием сил магнитного поля микротоки во всех атомах ориентируются определенным образом, создавая в теле допол­нительное магнитное поле. Результирующее магнитное поле, создаваемое всеми токами

(макро и микро) характеризуется вектором магнитной индукции 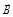. Следовательно, при од­ном и том же токе и прочих равных условиях вектор 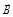будет иметь в различных средах разные значения.

Магнитное поле макротоков описывается вектором напряженности 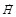. Для вакуума

Практически представление о данном магнитном поле изучается путем использования стальных опилок (как бы очень маленьких магнитных стрелок) и магнитной стрелки.

В₀ = μ₀ Н, где μ₀ =4π 10^-7 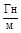магнитная постоянная. Для среды В = μ В₀, где μ - магнитная проницаемость среды, показывающая во сколько раз магнитное поле среды уси­ливается за счет поля микротоков среды.

ИЗМЕРЕНИЕ МАГНИТНОЙ ИНДУКЦИИ

Согласно теореме Стокса: циркуляция вектора напряженности 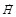по контуру L, охваты­вающим макроскопические токи 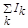равен:

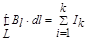или 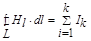- закон полного тока (2)

В и Н - проекции на направление I.

Закон полного тока позволяет вести расчеты в магнитных цепях. Например, для соле­ноида или тороида.

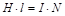
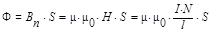, где

l - среднее значение длины линии магнитной индукции;

S - значение площади поперечного сечения;

I - ток одного витка;

N - число витков.

МАГНИТНОЕ ПОЛЕ МИКРОТОКОВ

Все вещества, помещенные в магнитное поле, намагничиваются. Рассмотрим причину этого явления с точки зрения строения атомов и молекул, положив в основу гипотезу Ампера, согласно которой в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Для качественного объяснения магнитных явлений с доста­точным приближением можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он об­ладает орбитальным магнитным моментом р_т = 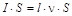, где 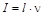- сила тока, S - площадь орбиты, ν - частота вращения электрона по орбите.

Экспериментально было доказано, что кроме орбитальных моментов электрон обладает СОБСТВЕННЫМ МЕХАНИЧЕСКИМ МОМЕНТОМ ИМПУЛЬСА, называемым спином (от англ. "spin" - "веретено"). Спину электрона соответствует СОБСТВЕННЫЙ (СПИНОВЫЙ) МАГНИТНЫЙ МОМЕНТ р_т . Первоначально существование спинов объяснялось тем, что электрон - заряженный шарик, вращающийся вокруг своей оси. Однако, вскоре это привело к противоречию. В настоящее время принимается, что собственный (спиновый) магнитный мо­мент является таким же неотъемлемым свойством электрона, как его масса и заряд.

Спином обладают не только электроны, но и другие элементарные частицы. Значения их

кратны целой и полуцелой величине ħ. В частности, для электрона M = 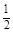ħ

ħ представляет собой естественную единицу изменения момента импульса " 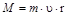", подобно тому как элементарный заряд "е" является естественной единицей за­ряда. Не отвлекаясь несложными расчетами получим, что проекция собственного спинового магнитного момента на направление вектора внешнего поля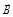

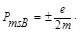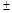
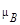ħ = (3)

Эту величину называют магнетоном Бора. И так, собственный магнитный момент электрона

равен одному магнетону Бора. Подставив значения величин, получим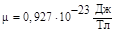

Магнитный момент атома слагается из орбитальных и собственных моментов электро­нов, магнитного момента ядра, обусловленного магнитными моментами протонов и нейтро­нов. Однако магнитные моменты ядер в тысячи раз меньше магнитных моментов электронов, так, например, масса ядра атома водорода в 1840 раз больше массы электрона. Поэтому маг­нитными моментами ядер при расчетах пренебрегают. Следовательно, магнитный момент ато­ма равен 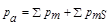(4)

В своих суждениях мы пользовались классическими представлениями, не учитывая огра­ничений, накладываемых на движение электронов законами квантовой механики (представ­ления - Боровские круговые орбиты, заряженные шарики и так далее). Для объяснения намаг­ничивания веществ существенно лишь то, что атомы обладают магнитными моментами.

ДИАМАГНЕТИКИ

Рассмотрим намагничивание диамагнитных веществ. К ним относятся многие металлы (Сu, Ag, Аu, Bi, ...), ртуть (Hg), вода (Н₂0), гелий (Не), углерод (С), стекло и подавляющее большинство органических соединений, смолы. Диамагнетиками называют вещества, суммар­ный магнитный момент атомов (молекул) которых равен нулю р_та = 0.

При внесении диамагнитного тела в магнитное поле ( 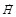) в нем будут индуцироваться микротоки, составляющая магнитного поля которых по правилу Ленца будет направлена про­тив внешнего магнитного поля. Например, против северного магнитного полюса возникнет се­верный магнитный полюс, в результате на диамагнетик будет действовать отталкивающая си­ла, диамагнетик вытолкнется из магнитного поля и суммарное магнитное поле, хотя и незначи­тельно, ослабеет. Например, для одного из сильнейших диамагнетиков, висмута (Bi) μ = 0,999824.

ПАРАМАГНЕТИКИ

Парамагнетиками называются вещества, магнитные моменты атомов (молекул) которых, в отсутствии внешнего магнитного поля, отлично от нуля ( 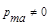), так как магнитные момен­ты электронов не компенсируют друг друга. Однако, вследствие теплового движения молекул их магнитные моменты в каждый момент времени ориентированы беспорядочно, поэтому па­рамагнитные вещества магнитными свойствами не обладают.

При внесении парамагнетика во внешнее магнитное поле магнитные силы поля стремят­ся установить магнитные моменты вдоль поля ( 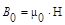). Однако, из-за теплового движе­ния произойдет незначительное намагничивание. Парамагнитные тела слабо, но притягивают­ся к магнитам. К парамагнитным телам относятся алюминий (Al), вольфрам (W), кислород, воздух. Для парамагнетиков μ 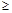1. Например, для жидкого кислорода μ = 1,0034 . Диамаг­нитный эффект наблюдается во всех телах, но в парамагнитных телах значительно слабее, чем парамагнитный.

НАМАГНИЧЕННОСТЬ

Для количественного описания намагничивания магнетиков вводят векторную величину - намагниченность J, определяемую магнитным моментом единицы объема магнетика:

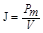, (5)

где 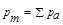- магнитный момент магнетика - векторная сумма магнитных моментов моле­кул. Согласно выше описанному, магнитной индукции результирующего магнитного поля в магнетике (В) равен векторной сумме магнитных индукций внешнего намагничивающего поля ( 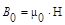), создаваемого намагничивающим током в вакууме и поля микротоков B_a.

Следовательно, В = В₀ + В_а. Для описания поля, создаваемого молекулярными токами, рассмотрим магнетик в виде кругового цилиндра сечением S, объемом V и длиной l, внесенного в однородное внешнее магнитное поле с индукцией 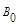. Возникающие в магнетике токи будут параллельны токам внешнего поля (для диамагнетиков направления токов и полей будут противоположны направлению внешних токов и поля).

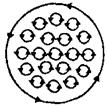В любом сечении цилиндра перпендикулярном его оси во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются. Нескомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра. Ток по боковой поверхности цилиндра подобен току в соленоиде и создает внутри поле, магнитную индукцию которого можно вычислить по формуле Стокса для соленоида из одного витка, 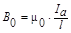, где I_a- молекулярный ток.

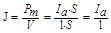- линеиная плотность тока.

Следовательно, 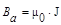, а 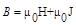. Как показывает опыт J пропорциональна Н: 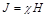, где χ - магнитная восприимчивость вещества. Тогда 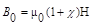, 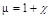(6)

Следовательно, согласно выражению ( 2 ) закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора В) 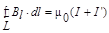,где I и I’ - алгебраические суммы

макротоков (токов проводимости) и микротоков (молекулярных токов).

ФЕРРОМАГНЕТИКИ

Особый класс магнетиков образуют вещества, способные обладать намагниченностью в отсутствии внешнего магнитного поля. Помещенные во внешнее магнитное поле они обладают рекордными значениями μ = 10¹⁰. Представителем этого класса является железо (Fe) и его сплавы. Поэтому они получили название ферромагнетиков. К их числу, кроме железа, относятся никель (Ni), кобальт (Со), гадолиний (Gd) и их сплавы - пермалой: сплав Ni - 78,5 % Fe - 21,5 % μ= 90000, супермалой: сплав Ni - 79 %, Mo - 5 %, Fe - 16 %, μ = 800000 , а так же некоторые сплавы и соединения марганца (Мn) и хрома (Сr) с ферромагнитными элементами. Ферромагнетизм присущ всем упомянутым веществам только в кристаллическом состоянии. Основы теории ферромагнетизма были развиты советским физиком Я.И. Френкелем и немецким физиком В.Гейзенбергом на основе квантовой теории. Описательная теория ферромагнетизма была разработана французским физиком П. Вейссом, Вейсс ввел гипотезу, согласно которой ферромагнетик ниже точки Кюри (см. ниже) разбивается на большее число малых макроскопических областей - доменов, самопроизвольно (спонтанно) намагниченных до точки насыщения. При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы хаотически и компенсируют друг друга, поэтому результирующий магнитный момент ферромагнетика равен нулю и ферромагнетик не намагничен. Даже внешнее относительно слабое магнитное поле ориентирует по направлению поля ( 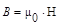) магнитные моменты не отдельных атомов, как это имело место в случае парамагнетиков, а целых областей спонтанной намагниченности (доменов). При ослаблении внешнего магнитного поля до нуля ферромагнетики сохраняют остаточное намагничение, так как тепловое движение не в состоя- ии быстро дезориентировать магнитные моменты столь крупных образований, какими явля­ется домены. Поэтому и наблюдается явление магнитного гистерезиса. Для того, чтобы ферро­магнетик размагнитить, необходимо приложить коэрцитивную (задерживающую) силу. Раз­магничиванию также способствуют удары, вибрационные движения и нагревание. Для каждого ферромагнетика имеется определенная температура (Т_к), при которой области спонтанного на­магничения распадаются и вещество утрачивает ферромагнитные свойства и становится обычным парамагнетиком. При охлаждении ниже Т_к в нем снова возникают до- Эта температура называется точкой Кюри (Т_к). Для Ni - T_k - 365° С, для Fe- Т_к = 753° С, для Со - Т_к = 1000° С.

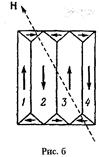Существование доменов в ферромагнетиках экспериментально дока­зано методом порошковых фигур (см. рис. б). На тщательно отполирован­ную поверхность ферромагнетика наносится водяная суспензия мельчайше­го ферромагнитного порошка. Частицы оседают преимущественно на гра­ницах между доменами. Подобную картину можно сфотографировать под микроскопом. Линейные размеры доменов оказались равными

10^-4 — 10^{-2 см. В настоящее время установлено, что магнитные свойства ферромагнетиков определяются спиновыми магнитными моментами электронов. Силы, возникающие при этом на­зываются обменными и имеют квантовую природу - она обусловлена волновыми свойствами электронов.}

Если для слабо магнитных ве­ществ зависимость J от Н линейная, то для ферромагнетиков эта зависимость является сложной. Эту зависимость для

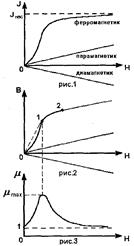железа впервые в 1878 году изучил русский физик А.И. Столетов методом баллистического гальванометра.

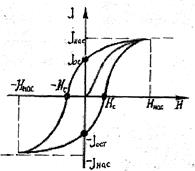
По мере возрастания Н намагниченность J сначала растет быстро, затем медленнее и, наконец, нарастание прекращается. Наступает так называемое магнитное насыщение. J нас не зави­сит от напряженности поля Н. Это явление объясняется тем, что по мере увеличения намагничивающего поля увеличивается сте­пень ориентации молекулярных магнитных моментов по направ­лению внешнего поля. Однако, этот процесс начнет замедляться, так как количество не ориентированных магнитных моментов остается все меньше и меньше. И наконец, когда все магнитные моменты будут ориентированы по направлению внешнего намагничивающего поля, дальнейшее увеличение J прекращается и наступает магнитное насыщение (смотри рис. 1)

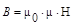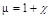, (см. 6), 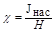(см.5)

Вначале μ, а следовательно B, растет с увеличением Н, достигая максимума, затем, стремится в случае сильных магнитных полей к единице, так как с увеличением Н ( 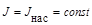) χ→0; μ→1 (смотри рис. 3). На рисунке 2 изображена кривая изменения магнитной индукции. Касательная к кривой в любой точке соответствует тангенсу угла наклона ее к кривой в данной точке и равна 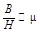(см. 6). Касательная 01 из начала координат соответствует максимальному значению тангенса, и следовательно максимальному значе­нию μ_max (смотри рис. 3). Кривая 01 соответствует возрастанию μ, а кривая 02 - убыванию.

Начиная с точки 2 наступает магнитное насыщение и кривая графика идет параллельно графику парамагнитного вещества, так как дальнейшее увеличение В может быть достигну­та только лишь за счет усиления внешнего намагничивающего поля 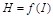, где I - намагничивающий ток.

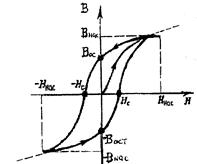
Характерная особенность ферромагнетиков состоит в том, что для них зависимость J от Н (а следовательно и В от Н) определяется предысторией намагничивания ферромагнетика. Это явление мы назвали выше магнитным гистерезисом. Если намагнитить ферромагнетик до насыщения (точка 1, см. рисунок), а затем начать уменьшать напряженность Н намагничивающего поля, то как показывает опыт, уменьшение J описывается кривой 1-2, лежащей выше кривой 1 - 0. J отличается от нуля при Н = 0, то есть в ферромагнетике наблюдается остаточное намагничение J_ос. С наличием остаточного намагничения связано существование постоянных магнитов. Намагничивание обращается в ноль под действием поля Н_с, имеющим направление, противоположное полю, вызвавшему намагничивание. Напряженность Н_с называется коэрцитивной силой. При дальнейшем увеличении противоположного поля ферромагнетик перемагничивается (кривая 3 - 4) и при H = H_нас достигает насыщения (точка 4). Затем ферромагнетик можно опять размагнитить (кривая 4 - 5 - 6) и вновь перемагнитить до насыщения (кривая 6 - 1). Таким образом, при действии на ферромагнетик переменного магнитного поля (переменного намагничивающего тока) намагниченность J изменяется периодически в соответствии с кривой 1 - 2 - 3 - 4 - 5 - 6 - 1, которая называется петлей гистерезиса (от греческого слова "запаздывание"). Нетрудно доказать, -о при одном цикле на перемагничивание ферромагнетика совершается на единицу объема работа 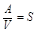- площадь петли гистерезиса. 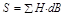. Тогда единицей измерения Н dB должна быть единица 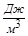. Проверим это.

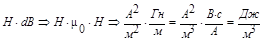- действительно так.

Различные ферромагнетики дают разные гистерезисные петли. Ферромагнетики с малой

площадью петли, с H_c всего лишь от нескольких тысячных до 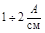(с узкой петлей гистерезиса), называются мягкими. Ферромагнетики с большой площадью петли и большей коэрцитивной силой от нескольких десятков до нескольких тысяч ампер на сантиметр (с широкой петлей гистерезиса) называются жесткими. Мягкие ферромагнетики применяются для изготовления сердечников трансформаторов и электрических машин. Например, сплав железа (Fe) с кремнием (Si) может иметь рекордное μ = 60000 и иметь большое омическое сопротивление для токов Фуко.

ОПРЕДЕЛЕНИЕ ТОЧКИ КЮРИ

Краткая теория

Кюри точка (температура Кюри, Т_с), температура фазового перехода второго рода, характеризующегося непрерывным изменением состояния вещества с приближением к точке фа­зового перехода и приобретением качественно нового свойства в этой точке. Названа по имени П. Кюри, подробно изучившего этот переход у ферромагнетиков.

При температуре Т ниже Кюри точки Т_с ферромагнетики обладают спонтанной намаг­ниченностью (Is) и определенной магнитно-кристаллической симметрией.

При нагреве ферромагнетика и приближении к точке Кюри усиливающееся тепловое движение атомов "расшатывает" существующий магнитный порядок одинаковую ориентацию магнитных моментов атомов.

В Кюри точке самопроизвольная намагниченность ферромагнетиков исчезает ( 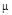=1), ферромагнетики становятся парамагнетиками.

Вблизи Кюри точки в веществе происходят специфические изменения многих физических свойств (например, теплоемкости, магнитной восприимчивости), достигающие максимума при Тк, что обычно и используется для точного определения температуры фазового перехода.

Если раскалить обычный стальной магнит до такой температуры, полностью исчезает не только намагниченность, но и все ферромагнитные свойства, в частности, разделение на доме­ны. Железо выше 770° С является парамагнитным.

Снижение температуры ниже т. Кюри возвращает ферромагнитные свойства - появляют­ся намагниченные до насыщения домены, магнитные моменты которых образуют замкнутые цепи. Таким образом, отожженный магнит надо намагничивать заново.

Проведение эксперимента

Приборы: эл. печь, 2 автотрансформатора, термопара, милливольтметр проградуированный на градусы, 2 катушки, микроамперметр, исследуемый образец (пермалой).

Ход работы

1. Собрать цепь по схеме:

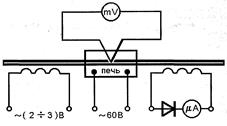2. Исследуемый образец поместить в установку. Термопару установить в центре печи.

3. На первичную катушку подать такое напряжение, чтобы стрелка микроамперметра в цепи вторичной катушки откланялась на 80-90% шкалы.

4. Подключить цепь и через каждые 10° С записывать показания микроамперметра.

5. По полученным данным построить график зависимости тока от температуры.

6. По графику определить точку Кюри.

7. Обратиться к учебнику А.В. Кортнев "Практикум по физике", работа № 55 на страни­це 31

ГРАФИК

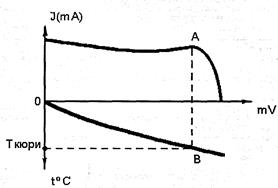Контрольные вопросы:

1. Как классифицируются магнетики?

2. Почему значение для ферромагнетиков велико?

3. Почему при определенной температуре ферромагнетики изменяют свои магнитные свойства?

4. Что такое точка Кюри?

5. Начертите и объясните схему установки?

6. Почему э.д.с. индукции во вторичной обмотке резко уменьшается при достижении об­разцом точки Кюри?

ИССЛЕДОВАНИЕ ПЕТЛИ ГИСТЕРЕЗИСА ФЕРРОМАГНЕТИКА

Краткая теория

Если напряженность внешнего поля увеличивать от нуля, то индукция поля в ферромагнетике, возрастая нелинейно, достигает насыщения B_н (рис. 1). При уменьшении напряженности до нуля поле в ферромагнетике имеет остаточную индукцию B_ост. Индукция в ферромагне­тике уменьшится до нуля при обратной напряженности поля Н_с, которая называется коэрци­тивной силой. Дальнейшее изменение напряженности сначала в сторону уменьшения, а затем увеличения позволяет достичь насыщения ферромагнетика в обратном направлении, а затем и в прямом. Полученная многозначная зависимость индукции магнитного поля в ферромагнетике от напряженности называется петлей гистерезиса.

Экспериментальная установка

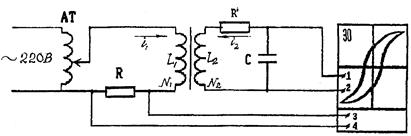Оборудование: электронный осциллограф, лабораторный автотрансформатор, трансформатор с двумя обмотками, два резистора, конденсатор, соединительные проводники, калька.

Принципиальная схема установки изображена на рисунке. На сердечнике в виде тора се­чением S = 3 10⁴мм², длина средней линии которого l = 210 мм, намотаны возбуждающая ка­тушка L1 из Ni = 2000 витков и индикаторная катушка L1 из N₁ = 1000 витков. 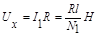Переменный ток I₁ в возбуждающей катушке создает магнитное поле напряженностью Н = N₁,I₁/ l.С резистора R на вход X осциллографа подается напряжение U_x, пропорциональное проходящему по этому резистору току и, следовательно, напряженности магнитного поля, создаваемого в сердечнике возбуждающей катушкой L1:

(1)

В индикаторной катушке L2 переменное магнитное поле индукцией В создает ЭДС индукции

,

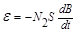которая вызывает вторичный ток I₂ , приближенно равный I₂ = 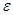/R’ , если считать, что индук­тивное сопротивление катушки и емкостное сопротивление конденсатора много меньше актив­ного сопротивления R’. Отсюда напряжение на конденсаторе C, которое подается на вход Y осциллографа:

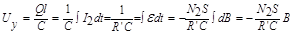(2)

Таким образом, осциллограф строит зависимость напряжение на конденсаторе С от на­пряжения на резисторе R, а эти напряжения пропорциональны соответственно индукции и на­пряженности магнитного поля. В результате на экране получается петля гистерезиса ферромаг­нитного сердечника.

Для количественных измерений масштабную сетку осциллографа нужно отградуировать по горизонтали в единицах напряженности (А/м), а по вертикали - в единицах индукции (Тл) магнитного поля.

Подадим на вход Y контрольное напряжение U_к осциллографа и измерим отклонение уча по вертикали у_к (половину вертикального отрезка). Тогда чувствительность осциллографа по вертикали равна 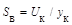(В/дел). Отсюда, если при получении петли гистерезиса отклонение по вертикали составило у, то согласно формуле (2) индукция равна

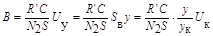. (3)

Аналогично чувствительность осциллографа по горизонтали 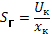(В/дел) и напряженность магнитного поля

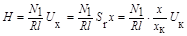. (4)

Проведение эксперимента

1. Заполните таблицу сведений о приборах.

№	Название прибора	Система прибора	Измеряемая величина	Единица измерения	Пределы измерения	Цена деления	Класс точности	Погрешность

2. Соберите установку по схеме, приведенной на рисунке. Включите осциллограф, установите оптимальную яркость и резкость линии на экране. Отключите горизонтальную развертку осциллографа для чего ручку "Ослабление" поставьте в положение "1:1".

3. Намагничивающий ток в возбуждающей катушке установите посредством автотрансформатора. Регуляторами усиления по горизонтали и вертикали добейтесь получения петли гистерезиса оптимального размера (около 3 см шириной и 8 см высотой). После этого до полного окончания работы не изменяйте чувствительность усилителей осциллографа.

4. Заготовьте по размеру экрана листок кальки, обозначьте на нем координатные оси и масштаб, наложите листок на экран осциллографа, так, чтобы оси экрана и листка совпали. полученную на экране гистерезисную петлю аккуратно скопируйте на кальку.

5. Отключите осциллограф от установки, поставьте переключатель "Ослабление" в положение "1:10" и подайте на вход Y контрольный сигнал с соответствующей клеммы осциллографа. По приведенной выше формуле определите чувствительность осциллографа по вертика­ли.

6. Переведите переключатель "Ослабление" в положение "1:1" и подайте контрольный сигнал на вход X. По приведенной выше формуле определите чувствительность осциллографа по горизонтали.

7. Напишите заключение.

Контрольные вопросы

1. Что такое магнитная индукция, как она связана с напряженностью магнитного поля?

2. В чем заключается явление намагничивания?

3. Объясните диамагнитные, парамагнитные и ферромагнитные явления.

4. Нарисуйте приблизительно кривые В(H) и J(H), в чем их различие?

5. Объясните явление намагничивания и получения кривой намагничивания (петли гистерезиса).

6. По какому закону изменяется напряженность магнитного поля в данной работе?

Литература

1.Курс общей физики. Т.Н. Трофимова.

2.Курс общей физики. И.В. Савельев. Том 2.

3.Курс общей физики. Г.А. Зисман.

4.Лекции по физике.