Волновые свойства микрочастиц

Высшего профессионального образования

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СТРОЕНИЕ АТОМА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К практическим занятиям

По курсу общей физики

Уфа 2005

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра физики

СТРОЕНИЕ АТОМА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям

по курсу общей физики

Уфа 2005

Составители: А.К. Хайретдинова, С.А. Шатохин

УДК 539.1(07)

ББК 22.383(Я7)

Строение атома: Методические указания к практическим занятиям по курсу общей физики. / Уфимск. гос. авиац. техн. ун-т; Сост.: А.К. Хайретдинова, С.А. Шатохин -Уфа, 2005. - 33 c.

Приведены примеры решения различных типов задач по темам практических занятий раздела «Атомная и ядерная физика».

Предназначены для студентов 1 и 2 курсов.

Библиогр.: 5 назв.

Рецензенты: А.С. Краузе,

Д.И. Косарева

© Уфимский государственный

авиационный

технический университет, 2005

Содержание

Введение........................................................................................................... 4

1. Атом Бора.................................................................................................... 5

Основные формулы........................................................................................ 5

Примеры решения задач................................................................................ 6

2. Волновые свойства микрочастиц ......................................................... 13

Основные формулы...................................................................................... 13

Примеры решения задач.............................................................................. 14

3. Элементы квантовой механики.............................................................. 20

Основные формулы...................................................................................... 20

Примеры решения задач.............................................................................. 21

4. Строение ядра. Энергии связи. Радиоактивность.............................. 26

Основные формулы...................................................................................... 26

Примеры решения задач.............................................................................. 28

Список литературы....................................................................................... 33

Введение

Практические занятия являются одной из важнейших компонент учебного процесса по физике. Они способствуют приобщению студентов к самостоятельной работе, учат анализировать изучаемые физические явления, использовать на практике полученные теоретические знания.

Предназначены для студентов, изучающих раздел курса общей физики «Атомная и ядерная физика». В методических указаниях представлены примеры решения типичных задач разной степени трудности. Решения сопровождаются необходимыми примерами и комментариями. Задачи систематизированы по основным темам раздела. По каждой теме приведены основные формулы, облегчающие усвоение алгоритмов решения задач.

Строение атома

Атом Бора

Основные формулы:

Первый постулат Бора: электроны в атоме могут двигаться только по определенным орбитам, находясь на которых они не излучают энергии. Эти орбиты называются стационарными и определяются условием

mυ_nr_n=nћ, (1.1)

где r_n – радиус n-ой орбиты, υ_n – скорость электрона на этой орбите; mυ_nr_n – момент импульса электрона, n – главное квантовое число (n=1, 2, 3…), ћ= , h – постоянная Планка, равная 6,62·10^-34 Дж·с.

Второй постулат Бора: при переходе электрона с одной орбиты на другую атом излучает или поглощает квант энергии, равный

hν=E_m-E_n, (1.2)

где E_m и E_n – энергии электрона на соответствующих орбитах.

Сериальная формула, определяющая длину волны света, излучаемого или поглощаемого атомом водорода при переходе из одного стационарного состояния в другое:

(1.3)

где R – постоянная Ридберга, равная 1,097·10⁷ м^-1, n и m – целые числа, называемые квантовыми.

Квантовое число n определяет серию спектральных линий: n=1 – серия Лаймана (ультрафиолетовое излучение), n=2 – серия Бальмера (видимое излучение), n=3 – серия Пашена (первая инфракрасная серия), n=4 – серия Брэкета (вторая инфракрасная серия), n=5 – серия Пфунда (третья инфракрасная серия).

Сериальная формула для длин волн линий спектра водородоподобных ионов (т.е. ионов, имеющих по одному электрону: He⁺, Li⁺⁺ и т.д.)

(1.4)

где z – порядковый номер элемента в таблице Менделеева.

Для рентгеновских спектров выполняется закон Мозли, согласно которому положение линий определяется соотношением

(1.5)

где σ – постоянная экранирования, n=1 соответствует K-серии, n=2 соответствует L-серии, n=3 соответствует M-серии Для K-серии σ=1.

Коротковолновая граница λ_min сплошного рентгеновского спектра определяется формулой

(1.6)

где e – заряд электрона, U – напряжение в рентгеновской трубке.

Примеры решения задач

Задача 1.1. Вычислить для атома водорода радиус первой боровской орбиты и период обращения электрона по этой орбите.

Решение. Радиус боровской орбиты r_n и скорость υ_n электрона на ней связаны соотношением (1.1). Чтобы иметь еще одно уравнение, связывающее эти величины, запишем второй закон Ньютона для электрона, который движется под действием кулоновской силы притяжения к ядру по круговой орбите.

Решая систему этих уравнений, получим

(1.7)

Полагаем n=1 (первая орбита)

(м)

Период обращения электрона по n-ой орбите равен

(1.8)

Скорость электрона, движущегося по первой орбите, определим из соотношения (1.7), подставив n=1.

(м/с).

Подставляем полученные соотношения для r₁ и υ₁ в (1.8)

(с).

Ответ: r₁=5,3·10^-11 м, T=1,5·10^-16 с.

Задача 1.2. Определить энергию фотона, соответствующего длинноволновой и коротковолновой границам серии Лаймана.

Решение.

На рисунке представлена система энергетических уровней атома водорода и переходы между уровнями, соответст-вующие серии Лаймана.

Из постулата Бора (1.2) следует, что наименьшей частоте (а, следовательно, и наибольшей длине волны) соответствует переход 1, а наибольшей частоте (наименьшей длине волны) – переход 2.

Используя формулу 1.3 и учитывая, что энергия фотона равна ε=hν, получим

(Дж)=10,2 (эВ)

; ε_max=hcR;

ε_max=6,62·10^-34·3·10⁸·1,097·10⁷=21,78·10^-19 (Дж)=13,6 (эВ).

Энергия фотона, соответствующая коротковолновой границе серии Лаймана в спектре излучения атома водорода (13,6 эВ) равна кванту энергии, поглощенному этим атомом при переходе электрона с первой орбиты на бесконечно удаленную орбиту (переход 3). Следовательно, энергия 13,6 эВ является энергией ионизации атома водорода.

ε_i=13,6 эВ. (1.9)

Зная энергию ионизации атома водорода, можно определить энергию фотона, соответствующего любой линии в спектре излучения или поглощения атома водорода и водородоподобных ионов по формуле

(эВ) (1.10)

Ответ: ε_min=10,2 эВ, ε_max=13,6 эВ.

Задача 1.3. Определить наименьшую скорость, которую должны иметь электроны, чтобы при возбуждении атома водорода ударами этих электронов в его видимой серии появились две линии.

Решение.

На диаграмме энергетических уровней показаны переходы, соответствующие двум линиям видимой серии.

2

Появлению этих линий должен предшествовать процесс возбуждения атома водорода, который в обычных условиях находится на первом энергетическом уровне. Чтобы в спектре появилась вторая линия (переход 2), атом водорода должен поглотить энергию (минимальную), равную (Е₄-Е₁) (переход 1 на рисунке). Эту энергию атому водорода передают при неупругом столкновении внешние электроны, обладающие кинетической энергией .

Согласно постулату Бора (1.2)

.

Применяем закон сохранения энергии:

.

Учитывая, что hcR=13,6 эВ=21,76·10^-19 Дж, получим

(м/с).

Ответ: υ=2,11·10⁶ м/с.

Задача 1.4. Первоначально покоящийся атом водорода испускает фотон с частотой 10¹⁵ Гц. Определить изменение полной энергии атома.

Решение.

Испустив фотон, атом приобрел скорость, которую можно определить, применяя к системе «фотон-атом» закон сохранения импульса. Первоначальный импульс системы равен нулю. После испускания фотона (импульс фотона ) атом приобрел импульс mυ.

. m=1,67·10^-27 кг – масса атома водорода. Если энергия атома до испускания фотона Е₀, а после испускания Е, то по закону сохранения энергии

.

Изменение энергии атома ΔЕ=Е₀-Е.

(Дж) = 4,14 эВ.

Ответ: ΔЕ = 4,14 эВ.

Задача 1.5. Свет от водородной лампы падает на дифракционную решетку с периодом 2,05 мкм. Под углом 30° зарегистрирована некоторая линия десятого порядка. Определить, какому переходу электрона в атоме водорода соответствует эта линия.

Решение.

Условием главного максимума при дифракции решетки является соотношение d·sinφ=kλ, из которого следует, что длина волны, излучаемой атомом водорода линии равна

; (мкм)=102,5 нм.

Найденная длина волны свидетельствует о том, что эта линия наблюдается в ультрафиолетовой области спектра. Применим сериальную формулу для этой области спектра , откуда можно определить n – номер уровня, с которого перешел электрон

Ответ: электрон перешел с третьего уровня на первый.

Задача 1.6. Атом водорода в основном состоянии поглотил фотон с энергией 12,75 эВ. Сколько линий будет содержать спектр атома водорода, и каким сериям принадлежат эти линии? Определить их длины волн.

Решение.

Применим формулу (1.10), считая, что нам известна энергия ионизации атома водорода: ε_i=13,6 эВ. В этой формуле ε – энергия поглощенного фотона

,

откуда Следовательно, электрон перешел с первого уровня на четвертый (см. рис.). Все возможные переходы электрона при возвращении атома водорода в исходное состояние изображены на рисунке: их 6, следовательно, спектр атома содержит 6 линий. Из этих линий 3 принадлежат серии Лаймана (1, 2, 3), 2 – серии Бальмера (4, 5) и 1 – серии Пашена (6).

нм.

нм.

λ₃=97,2 нм. λ₄=656 нм.

λ₅=486 нм. λ₆=1875 нм.

Ответ: (нм), (нм), λ₃=97,2 нм, λ₄=656 нм, λ₅=486 нм, λ₆=1875 нм.

Задача 1.7. Фотон первой линии серии Лаймана иона гелия (Не⁺) поглощается атомом водорода, находящемся в основном состоянии и ионизирует его. Определить кинетическую энергию, которую получил электрон при ионизации.

Решение.

Из закона сохранения энергии следует, что энергия фотона, испускаемого ионом гелия, расходуется на работу ионизации атома водорода и на сообщение кинетической энергии оторвавшемуся от атома Н электрону.

.

Энергия, необходимая для ионизации атома водорода равна hcR=13,6 эВ.

Для определения энергии фотона гелия Не⁺ используем сериальную формулу для водородоподобных ионов (1.4), где Z=2 для гелия, а n=2 для первой линии спектра Лаймана

(hν)_Не=3hcR.

Закон сохранения перепишем в виде

,

откуда эВ.

Ответ: E_k=27,2 эВ.

Задача 1.8. Антикатод рентгеновской трубки покрыт молибденом (Z=42). Определить минимальную разность потенциалов, которую надо приложить к трубке, чтобы в спектре рентгеновского излучения появились линии K-серии молибдена.

Решение.

K-серия возникает при переходе электронов на самый глубокий слой K (n=1) с менее глубоких электронных слоев L (n=2), M (n=3) и т.д. Но, чтобы любой из этих переходов стал возможным, необходимо появление вакантного места в K -слое.

Для этого один из двух электронов K –слоя должен быть вырван из атома (или переведен на внешний, не заполненный электронами слой), т.к. слои L, M и т.д. целиком заполнены электронами.

Минимальную энергию, необходимую для удаления электрона K –слоя из атома, можно оценить, используя закон Мозли (1.5). Действительно, квант энергии характеристических рентгеновских лучей равен

.

Положив n=1 и m =∞ и учитывая, что для K –серии σ=1, получим

hν=hcR(Z-1)².

Очевидно, что такую же энергию должен поглотить атом при обратном процессе – вырывании электрона из K –слоя, что необходимо для появления линий K –серии. Эту энергию атом молибдена получает в результате удара об антикатод электрона, обладающего энергией .

Разность потенциалов U будет минимальной, когда вся энергия электрона поглощается атомом, т.е.

hν=eU; hcR(Z-1)²=eU_min,

откуда ; hcR=13,6 эВ;

(В) ≈ 23 кВ.

Ответ: U_min≈23 кВ.

Волновые свойства микрочастиц

Основные формулы:

Формула де-Бройля

, (2.1)

где λ – длина волны, связанная с частицей, имеющей импульс p=mυ.

Связь длины волны де-Бройля с кинетической энергией E_k имеет вид:

а) в классическом приближении (E_k<<m₀c²) p=mυ,

откуда (2.2)

б) в релятивистском случае (E_k~m₀c²)

E_k=mc²-m₀c²=E- m₀c²,

E²=( m₀c²)²+p²c²,

где E и E_k – полная и кинетическая энергии соответственно. Таким образом, релятивистский импульс равен

,

соответственно

(2.3)

Соотношение неопределенностей:

1) для координаты и импульса , (2.4)

где Δp_x – неопределенность проекции импульса частицы на ось x; Δх – неопределенность ее координаты;

2) для энергии и времени (2.5)

где ΔЕ – неопределенность энергии данного квантового состояния, Δτ – время пребывания системы в этом состоянии.

Примеры решения задач

Задача 2.1. Кинетическая энергия протона в 4 раза меньше его энергии покоя (E₀=m₀c²=1,5·10^-10 Дж). Вычислить длину волны де-Бройля.

Решение.

Поскольку по условию задачи кинетическая энергия сравнима с его энергией покоя, то импульс p и кинетическая энергия связаны соотношением

.

С учетом условия задачи E_k=E₀/4 получим

и,

следовательно,

.

Подставляя числовые значения, получим

(м).

Ответ: 1,77·10^-15 м.

Задача 2.2. Определить длину волны де-Бройля электронов, обладающих кинетической энергией: 1) 100 эВ; 2) 0,5 МэВ.

Решение.

Как видно из формулы 2.1, определение де-Бройлеровской длины волны сводится к нахождению импульса (mυ) частицы. Решение задачи зависит от того, является ли электрон классической или релятивистской частицей.

1) В этом случае E_k=m₀c², поэтому длину волны де-Бройля следует определять по формуле 2.3.

(м) = 1,4 пм.

2) Так как E_k<<m₀c², где m₀c²=0,51 МэВ – энергия покоя электрона, то в данном случае электрон является классической частицей, следовательно, его импульс и кинетическая энергия связаны соотношением 2.2, тогда длина волны де-Бройля равна

(м) = 123 пм.

Ответ: λ₁= 1,4 пм, λ₂= 123 пм.

Задача 2.3. Определить длину волны де-Бройля электронов при соударении с которыми в серии Пашена спектра излучения атома водорода появились две линии.

Решение.

Как видно из рисунка, чтобы в серии Пашена появились две линии, атом водорода должен быть возбужден до пятого уровня, т.е. минимальная энергия, которую получил атом водорода, равна ΔЕ = Е₅ - Е₁. Эту энергию атому передали электроны, де-Бройлевскую длину волны которых надо определить.

Следовательно,

,

откуда

и длина волны де-Бройля (2.1)

Учитывая, что hcR = 13,6 (эВ) = 13,6·1,6·10^-19 (Дж), получим

(м).

Ответ: λ=3,4·10^-10 м.

Задача 2.4. Параллельный пучок электронов падает нормально на диафрагму с узкой прямоугольной щелью шириной 2 мкм. Определить скорость электронов (считая ее одинаковой для всех частиц), если известно, что на экране, отстоящем от щели на расстоянии 50 см, ширина центрального дифракционного максимума равна 80 мкм.

Решение.

Дифракция электронов является следствием волновой природы частиц. Поэтому для определения скорости электронов применим формулу де-Бройля (2.1), откуда

.

Чтобы найти длину волны λ, воспользуемся тем обстоятельством, что дифракционная картина, возникающая при прохождении через узкую щель параллельного пучка электронов, вполне соответствует дифракционной картине, полученной от этой же щели при освещении пучком монохроматического света, длина волны которого равна длине волны де-Бройля. Это значит, что в случае дифракции электронов положение дифракционных максимумов и минимумов можно определять по формулам для длины волны света.

На рисунке изображена кривая распределения интенсивности на экране, расположенном на расстоянии ℓ от щели, ширина которой а.

Центральный максимум заключен между двумя минимумами первого порядка. Ширина центрального максимума b. φ – угол дифракции, соответствующий первому минимуму. Условие, определяющее положение дифракционных минимумов

a·sinφ=kλ, (в нашем случае k=1).

Откуда sinφ=λ/а.

Из рисунка видно, что .

Угол дифракции, соответствующий первому минимуму, мал, поэтому tgφ≈sinφ

,

откуда

и скорость электронов определяется по формуле

(м/с).

Ответ: υ=4,5·10⁶ м/с.

Задача 2.5. Средняя кинетическая энергия электрона в невозбужденном атоме водорода 13,6 эВ. Исходя из соотношения неопределенностей, оценить наименьшую неточность, с которой можно вычислить координату электрона в атоме.

Решение.

Как следует из соотношения неопределенностей (2.4), неточность координаты частицы

(1)

Рассматривая электрон как нерелятивистскую частицу (так как 13,6 эВ<<m₀c²) получим для импульса электрона

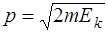(2)

Сравним величины Δp_x и p. Импульс p – векторная величина и направление его неизвестно. Поэтому проекция p_x импульса на какую-либо ось x оказывается неопределенной: ее величина лежит в интервале (-p, p), т.е. неопределенность проекции импульса на ось x равна

Δp_x=2p или Δp_x~ p

И наименьшая неточность координаты будет соответствовать Δp_x=p. С учетом сказанного и в соответствии с (2) имеем

(м).

Как видно из расчета, Δx равен радиусу первой боровской орбиты (r). Отсюда следует, что боровскую орбиту нельзя представлять как траекторию, по которой движется электрон, т.к. он может оказаться в любом месте атома, находящегося в определенном (в данном случае – не возбужденном) состоянии, а не только на расстоянии r от ядра. r – это наиболее вероятное расстояние, на котором можно встретить электрон в атоме.

Ответ: 0,53·10^-10 (м).

Задача 2.6. Электрон с кинетической энергией E_k=10 эВ находится в металлической пылинке диаметром d=1 мкм. Оценить в процентах относительную неопределенность скорости электрона.

Решение.

Относительная неопределенность скорости и импульса связаны соотношением

.

Неопределенность импульса можно оценить из соотношения неопределенности, а именно

.

Поскольку в данном случае E_k<<m₀c², то величина импульса электрона определяется выражением

.

Таким образом

.

Ответ: 0,0062 %.

Задача 2.7. Используя соотношение неопределенностей Гейзенберга, оценить естественную ширину Δλ спектральной линии атома водорода, соответствующей длинноволновой границе серии Пашена.

Решение.

В данном случае необходимо применить соотношение неопределенностей для энергии и времени (2.5). Так как энергия излучаемого фотона E=hν или E=h , то разброс в значениях длин волн Δλ (ширина спектральной линии) является следствием разброса (неопределенности) в энергии излучаемых фотонов (ΔE). В свою очередь, ΔEсвязана с неопределенностью энергии атома (ΔЕ), т.е. шириной энергетического уровня, которую можно определить из соотношения (2.5):

,

где Δτ – среднее время жизни возбужденного состояния атома, равное 10^-8 с.

Продифференцировав соотношение E = , получим

ΔE= ,

откуда (1).

По условию задачи λ соответствует длинноволновой границе серии Пашена. Применяя сериальную формулу (1.3) (n=3, m=4), получим

,

откуда (нм).

Подставляем полученное значение λ в (1)

(м) = 18,7 пм.

Ответ: Δλ=18,7 пм.