Световой поток. Связь между энергетическими и световыми величинами

Определения фотометрических величин светового ряда и математические соотношения между ними аналогичны соответствующим величинам и соотношениям энергетического ряда. Поэтому световой поток 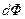, распространяющийся в пределах телесного угла 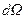, равняется 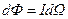. Единица измерения светового потока 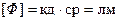(люмен). Для монохроматического света связь между энергетическими и световыми величинами дается формулами:

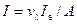, (30.6)

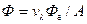, (30.7)

где 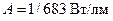– константа, называемая механическим эквивалентом света.

Световой поток, приходящийся на интервал длин волн от l до ,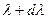

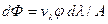, (30.8)

где j – функция распределения энергии по длинам волн (см. рис. 30.1). Тогда полный световой поток, переносимый всеми волнами спектра,

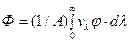. (30.9)

Освещенность

Световой поток может исходить и от тел, которые сами не светятся, а отражают или рассеивают падающий на них свет. В таких случаях важно знать, какой световой поток падает на тот или иной участок поверхности тела. Для этого служит физическая величина, называемая освещенностью

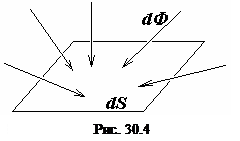
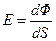. (30.10)

Освещенность численно равняется отношению полного светового потока 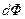, падающего на элемент поверхности, к площади 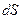этого элемента (см. рис. 30.4). Для равномерного светового потока

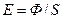. (30.11)

Единица измерения освещенности 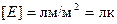(люкс). Люкс равняется освещенности поверхности площадью 1 м², когда на неё падает световой поток 1 лм. Аналогично определяется энергетическая освещенность

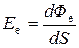(30.12)

или

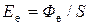. (30.13)

Единица энергетической освещенности .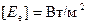

Яркость

Для многих светотехнических расчетов некоторые источники можно рассматривать как точечные. Однако, в большинстве случаев источники света размещены достаточно близко, чтобы можно было различить их форму, иначе говоря, угловые размеры источника лежат в пределах способности глаза или оптического инструмента отличить протяженный предмет от точки. Для таких источников вводится физическая величина, называемая яркостью. Понятие яркости неприменимо к источникам, угловые размеры которых меньше разрешающей способности глаза или оптического инструмента (например, к звездам). Яркость характеризует излучение светящейся поверхности в определенном направлении. Источник может светиться собственным или отраженным светом.

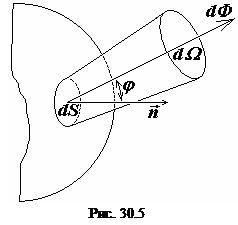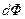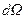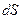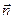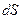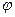Выделим световой поток , распространяющийся в определенном направлении в телесном угле от участка светящейся поверхности . Ось пучка образует с нормалью к поверхности угол (см. рис. 30.5).

Проекция участка 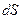светящейся поверхности на площадку, перпендикулярную к выбранному направлению,

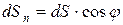(30.14)

называется видимой поверхностью элемента площадки 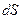источника (см. рис. 30.6).

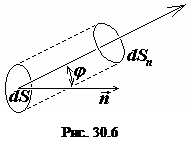Значение светового потока 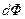зависит от площади видимой поверхности, от угла 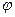и от телесного угла :

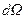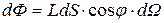. (30.15)

Коэффициент пропорциональности 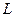называется яркостью, Он зависит от оптических свойств излучающей поверхности и может быть разным для различных направлений. Из (30.5) яркость

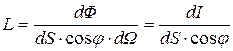. (30.16)

Таким образом, яркость определяется световым потоком, испускаемым в определенном направлении единицей видимой поверхности в единичный телесный угол. Или иначе: яркость в определенном направлении численно равняется силе света, создаваемой единицей площади видимой поверхности источника.

В общем случае яркость зависит от направления, но существуют источники света, для которых яркость от направления не зависит. Такие источники называются ламбертовскими или косинусными, потому что для них справедлив закон Ламберта: сила света в некотором направлении пропорциональна косинусу угла между нормалью к поверхности источника и этим направлением:

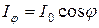, (30.17)

где 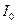– сила света в направлении нормали к поверхности, 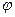– угол между нормалью к поверхности и выделенным направлением. Для обеспечения одинаковой яркости во всех направлениях технические светильники снабжают оболочками из молочного стекла. К ламбертовським источникам, испускающим рассеянный свет, относятся поверхность, покрытая оксидом магния, неглазированный фарфор, чертежная бумага, свежевыпавший снег.

Единица яркости 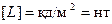(нит). Приведем значения яркости некоторых источников света:

Луна – 2,5 кнт,

люминесцентная лампа – 7 кнт,

нить накала электрической лампочки – 5 Мнт,

поверхность Солнца – 1,5 Гнт.

Наименьшая яркость, воспринимаемая глазом человека, – около 1 мкнт, а яркость, превышающая 100 кнт, вызывает болевое ощущение в глазу и может повредить зрение. Яркость листа белой бумаги при чтении и письме должна быть не меньшей 10 нт.

Аналогично определяется энергетическая яркость

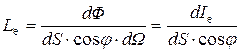. (30.18)

Единица измерения энергетической яркости .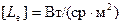

Светимость

Рассмотрим источник света конечных размеров (светящий собственным или отраженным светом). Светимостью 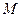источника называется поверхностная плотность светового потока, испускаемого поверхностью во всех направлениях в пределах телесного угла 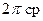. Если элемент поверхности 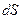испускает световой поток 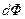, то

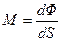. (30.19)

Для равномерной светимости можно записать:

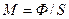. (30.20)

Единица измерения светимости .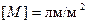

Аналогично определяется энергетическая светимость

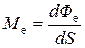. (30.21)

Единица энергетической светимости .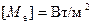

Законы освещенности

Фотометрические измерения базируются на двух законах освещенности.

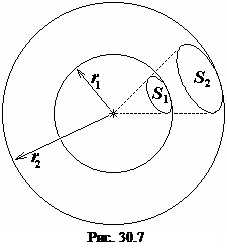
1. Освещенность поверхности точечным источником света изменяется обратно пропорционально квадрату расстояния источника от освещаемой поверхности. Рассмотрим точечный источник 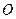(см. рис. 30.7), испускающий свет во всех направлениях. Опишем вокруг источника концентрические с источником сферы радиусам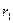и и 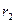. Очевидно, что световой поток через участки поверхносте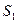й и 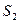одинаков, так как он распространяется в одном телесном угле 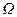. 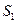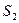Тогда освещенность участков и составит, соответственно, 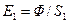и 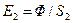. Выразив элементы сферических поверхностей через телесный угол 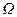, получаем:

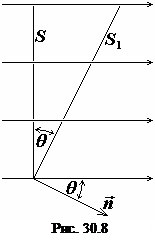
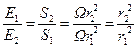. (30.22)

2. Освещенность, создаваемая на элементарном участке поверхности световым потоком, падающим на него под некоторым углом, пропорциональна косинусу угла между направлением лучей и нормалью к поверхности. Рассмотрим параллельный пучок лучей (см. рис. 29.8), падающих на участки поверхносте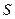й и 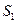. На поверхность 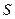лучи падают по нормали, а на поверхность 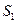– под углом 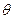к нормали. Через оба участка проходит одинаковый световой поток 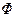. Освещенность первого и второго участков составит, соответственно, 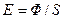и . 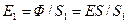Но 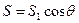, поэтому,

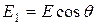. (30.23)

Объединив эти два закона, можно сформулировать основной закон освещенности: освещенность поверхности точечным источником прямо пропорциональна силе света источника, косинусу угла падения лучей и обратно пропорциональна квадрату расстояния от источника до поверхности

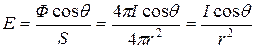. (30.24)

Расчеты по этой формуле дают достаточно точный результат, если линейные размеры источника не превышают 1/10 расстояния до освещаемой поверхности. Если источником является диск диаметром 50 см, то в точке на нормали к центру диска относительная погрешность в расчетах для расстояния 50 см достигает 25%, для расстояния 2 м она не превышает 1,5%, а для расстояния 5 м уменьшается до 0,25%.

Если источников несколько, то результирующая освещенность равняется сумме освещенностей, создаваемых каждым отдельным источником. Если источник нельзя рассматривать как точечный, его поверхность делят на элементарные участки и, определив освещенность, создаваемую каждым из них, по закону 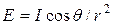, интегрируют затем по всей поверхности источника.

Существуют нормы освещенности для рабочих мест и помещений. На столах учебных помещений освещенность должна быть не меньше 150 лк, для чтения книг нужна освещенность 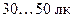, а для черчения – 200 лк. Для коридоров достаточной считается освещенность 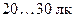, для улиц – .

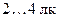Важнейший для всего живого на Земле источник света – Солнце создает на верхней границе атмосферы энергетическую освещенность, называемую солнечной постоянной – 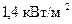и освещенность 137 клк. Энергетическая освещенность, создаваемая на поверхности Земли прямыми лучами летом в два раза меньше. Освещенность, создаваемая прямыми солнечными лучами в полдень на средней широте местности, составляет 100 клк. Смена времен года на Земле объясняется изменением угла падения солнечных лучей на её поверхность. В северном полушарии наибольшим угол падения лучей на поверхность Земли бывает зимой, а наименьшим – летом. Освещенность на открытом месте при облачном небе составляет 1000 лк. Освещенность в светлой комнате вблизи окна – 100 лк. Для сравнения приведем освещенность от полной Луны – 0,2 лк и от ночного неба в безлунную ночь – 0,3 млк. Расстояние от Солнца до Земли составляет 150 миллионов километров, но благодаря тому, что сила солнечного света равняется 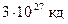, освещенность, создаваемая Солнцем на поверхности Земли, так велика.

Для источников, сила света которых зависит от направления, иногда пользуются средней сферической силой света 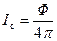, где 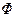– полный световой поток лампы. Отношение светового потока 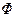электрической лампы к её электрической мощности 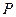называют световой отдачей 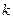лампы: 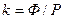. Например, лампа накаливания мощностью 100 Вт имеет среднюю сферическую силу света около 100 кд. Полный световой поток такой лампы 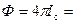4×3,14×100 кд = 1260 лм, а световая отдача равняется 12,6 лм/Вт. Световая отдача ламп дневного света в несколько раз больше, чем у ламп накаливания, и достигает 80 лм/Вт. К тому же срок службы люминесцентных ламп превышает 10 тыс. часов, тогда как для ламп накаливания он меньше 1000 часов.

За миллионы лет эволюции человеческий глаз приспособился к солнечному свету, и поэтому желательно, чтобы спектральный состав света лампы был как можно ближе к спектральному составу солнечного света. Этому требованию в наибольшей степени отвечают люминесцентные лампы. Именно поэтому их называют также лампами дневного света. Яркость нити накала электрической лампочки вызывает болевое ощущение в глазу. Для предупреждения этого используют плафоны из молочного стекла и абажуры.

При всех своих преимуществах люминесцентные лампы имеют и ряд недостатков: сложность схемы включения, пульсация светового потока (с частотою 100 Гц), невозможность запуска на морозе (вследствие конденсации ртути), гудение дросселя (вследствие магнитострикции), экологическая опасность (ртуть из разбитой лампы отравляет окружающую среду).

Для того чтобы спектральный состав излучения лампы накаливания был таким, как у Солнца, нужно было бы раскалить её нить до температуры поверхности Солнца, т. е. до 6200 К. но вольфрам – наиболее тугоплавкий из металлов – плавится уже при 3660 К.

Температура, близкая к температуре поверхности Солнца, достигается в дуговом разряде в парах ртути или в ксеноне под давлением около 15 атм. Силу света дуговой лампы можно довести до 10 Мкд. Такие лампы используются в кинопроекторах и прожекторах. Лампы, заполненные парами натрия, отличаются тем, что в них значительная часть излучения (около трети) сконцентрирована в видимой области спектра (две интенсивных желтых линии 589,0 нм и 589,6 нм). Хотя излучение натриевых ламп сильно отличается от привычного для человеческого глаза солнечного света, они используются для освещения автострад, так как их преимуществом является высокая световая отдача, достигающая 140 лм/Вт.

Фотометры

Приборы, предназначенные для измерения силы света или световых потоков разных источников, называются фотометрами. По принципу регистрации фотометры бывают двух типов: субъективные (визуальные) и объективные.

Принцип действия субъективного фотометра основывается на способности глаза с достаточно большой точностью фиксировать одинаковость освещенностей (точнее, яркостей) двух смежных полей при условии, что они освещены светом одинакового цвета.

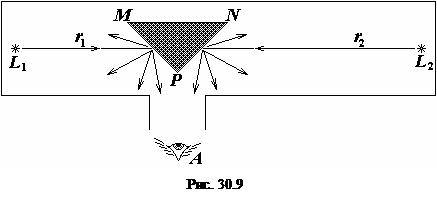Фотометры для сравнения двух источников устроены так, что роль глаза сводится к установлению одинаковости освещенностей двух смежных полей, освещаемых сравниваемыми источниками (см. рис. 30.9). Глаз наблюдателя 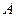рассматривает белую трехгранную призму 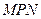, установленную посредине зачерненной внутри трубы. Призма освещается источникам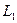и и 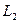. Изменяя расстояния 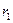и 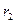от источников до призмы, можно уравнять освещенности поверхносте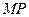й и 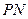. 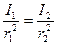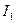Тогда , где и 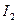– силы света, соответственно, источников 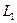и 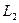. Если сила света одного из источников известна (эталонный источник), то можно определить силу света другого источника в выбранном направлении. Измерив силу света 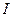источника в разных направлениях, находят суммарный световой поток 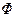, освещенность 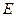и т. д. Эталонный источник представляет собой лампу накаливания, сила света которой известна.

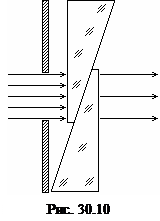
Невозможность в очень широких пределах изменять отношение расстояний вынуждает использовать другие способы ослабления потока, такие как поглощение света фильтром переменной толщины – клином (см. рис.30.10).

Одной из разновидностей визуального метода фотометрии является метод гашения, основывающийся на использовании постоянства пороговой чувствительности глаза для каждого отдельного наблюдателя. Пороговой чувствительностью глаза называют наименьшую яркость (около 1 мкнт), на которую реагирует человеческий глаз. Определив предварительно порог чувствительности глаза, каким-нибудь способом (например, калиброванным поглощающим клином) ослабляют яркость исследуемого источника до порога чувствительности. Зная, во сколько раз ослаблена яркость, можно определить абсолютную яркость источника без эталонного источника. Этот метод отличается чрезвычайно высокой чувствительностью.

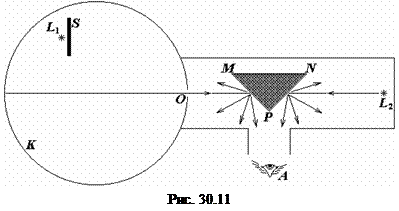Непосредственное измерение полного светового потока источника осуществляется в интегральных фотометрах, например, в сферическом фотометре (см. рис. 30.11). Исследуемый источник 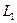подвешивается во внутренней полости побеленной внутри матовой поверхностью сферы 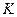. В результате многократных отражений света внутри сферы создается освещенность, определяемая средней силой света источника. Освещенность отверстия 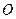, защищенного от прямых лучей экраном 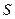, пропорциональна световому потоку: 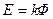, где 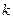– константа прибора, зависящая от его размеров и окраски. Отверстие 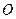покрыто молочным стеклом. Яркость молочного стекла также пропорциональна световому потоку 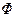. Её измеряют описанным выше фотометром или другим способом. В технике применяются автоматизированные сферические фотометры с фотоэлементами, например для контроля ламп накаливания на конвейере электролампового завода.

Объективные методы фотометрии разделяются на фотографические и электрические. Фотографические методы основываются на том, что почернение светочувствительного слоя в широких пределах пропорционально плотности световой энергии, упавшей на слой во время его освещения, т. е. экспозиции 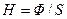(см. табл. 30.1). Этим методом определяют относительную интенсивность двух близко расположенных спектральных линий в одном спектре или сравнивают интенсивности одной и той же линии в двух смежных (снятых на одну фотопластинку) спектрах по почернению определенных участков фотопластинки.

Визуальные и фотографические методы постепенно вытесняются электрическими. Преимуществом последних является то, что в них достаточно просто осуществляется автоматическая регистрация и обработка результатов, вплоть до использования компьютера. Электрические фотометры дают возможность измерять интенсивность излучения и за пределами видимого спектра.

ГЛАВА 31. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ

31.1. Характеристики теплового излучения

Тела, нагретые до достаточно высоких температур, светятся. Свечение тел, обусловленное нагреванием, называется тепловым (температурным) излучением. Тепловое излучение, являясь самым распространенным в природе, совершается за счет энергии теплового движения атомов и молекул вещества (т. е. за счет его внутренней энергии) и свойственно всем телам при температуре выше 0 К. Тепловое излучение характеризуется сплошным спектром, положение максимума которого зависит от температуры. При высоких температурах излучаются короткие (видимые и ультрафиолетовые) электромагнитные волны, при низких — преимущественно длинные (инфракрасные).

Количественной характеристикой теплового излучения служит спектральная плотность энергетической светимости (излучательности) тела — мощность излучения с единицы площади поверхности тела в интервале частот единичной ширины:

R_v,T = 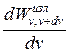, (31.1)

где 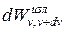— энергия электромагнитного излучения, испускаемого за единицу времени (мощность излучения) с единицы площади поверхности тела в интервале частотот v доv+dv.

Единица спектральной плотности энергетической светимости R_v,T — джоуль на метр в квадрате (Дж/м²).

Записанную формулу можно представить в виде функции длины волны:

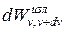= R_v,T dv= R_λ,T dλ. (31.2)

Так как с =λvυ, то dλ/ dv = - с/ v²= - λ²/с,

где знак минус указывает на то, что с возрастанием одной из величин (λ или v) другая величина убывает. Поэтому в дальнейшем знак минус будем опускать.

Таким образом,

R_υ,T =R_λ,T 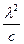. (31.3)

С помощью формулы (31.3) можно перейти от R_v,T к R_λ,T и наоборот.

Зная спектральную плотность энергетической светимости, можно вычислить интегральную энергетическую светимость (интегральную излучательность), просуммировав по всем частотам:

R_T = 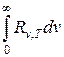. (31.4)

Способность тел поглощать падающее на них излучение характеризуется спектральной поглощательной способностью

А_v,T = 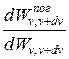(31.5)

показывающей, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частотами от v доv+dv, поглощается телом.

Спектральная поглощательная способность — величина безразмерная. Величины R_v,T и А_v,T зависят от природы тела, его термодинамической температуры и при этом различаются для излучений с различными частотами. Поэтому эти величины относят к определенным Т и v (вернее, к достаточно узкому интервалу частот от v доv+dv).

Тело, способное поглощать полностью при любой температуре все падающее на него излучение любой частоты, называется черным. Следовательно, спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице (А^ч_v,T =1). Абсолютно черных тел в природе нет, однако такие тела, как сажа, платиновая чернь, черный бархат и некоторые другие, в определенном интервале частот по своим свойствам близки к ним.

Идеальной моделью черного тела является замкнутая полость с небольшим отверстием, внутренняя поверхность которой зачернена (рис.31.1). Луч света, попавший внутрь Рис.31.1.

такой полости, испытывает многократные отражения от стенок, в результате чего интенсивность вышедшего излучения оказывается практически равной нулю. Опыт показывает, что при размере отверстия, меньшего 0,1 диаметра полости, падающее излучение всех частот полностью поглощается. Вследствие этого открытые окна домов со стороны улицы кажутся черными, хотя внутри комнат достаточно светло из-за отражения света от стен.

Наряду с понятием черного тела используют понятие серого тела — тела, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры, материала и состояния поверхности тела. Таким образом, для серого тела А^с_v,T <1.

Закон Кирхгофа

Закон Кирхгофа: отношение спектральной плотности энергетической светимости к спектральной поглощательной способности не зависит от природы тела; оно является для всех тел универсальной функцией частоты (длины волны) и температуры:

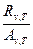= r_v,T (31.6)

Для черного тела А^ч_v,T =1, поэтому из закона Кирхгофа вытекает, что R_v,T для черного тела равна r_v,T. Таким образом, универсальная функция Кирхгофа r_v,T есть не что иное, как спектральная плотность энергетической светимости черного тела. Следовательно, согласно закону Кирхгофа, для всех тел отношение спектральной плотности энергетической светимости к спектральной поглощательной способности равно спектральной плотности энергетической светимости черного тела при той же температуре и частоте.

Из закона Кирхгофа следует, что спектральная плотность энергетической светимости любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости черного тела (при тех же значеннях Т и v), так как А_v,T < 1, и поэтому R_v,T < r v_υ,T. Кроме того, из (31.6) вытекает, что если тело при данной температуре Т не поглощает электромагнитные волны в интервале частот от v, до v+dv, то оно их в этом интервале частот при температуре Т и не излучает, так как при А_v,T=0, R_v,T=0

Используя закон Кирхгофа, выражение для интегральной энергетической светимости черного тела (31.4) можно записать в виде

R_T= 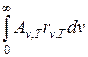. (31.7)

Для серого тела R^с_T = А_T 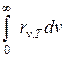= А_TR_е, (31.8)

где R_е = 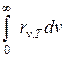-энергетическая светимость черного тела.

Закон Кирхгофа описывает только тепловое излучение, являясь настолько характерным для него, что может служить надежным критерием для определения природы излучения. Излучение, которое закону Кирхгофа не подчиняется, не является тепловым.

Для практических целей из закона Кирхгофа следует, что тела, обладающие темной и шероховатой поверхностью, имеют коэффициент поглощения, близкий к 1. По этой причине зимой предпочитают носить темную одежду, а летом – светлую. Но тела, имеющие коэффициент поглощения, близкий к единице, обладают и соответственно большей энергетической светимостью. Если взять два одинаковых сосуда, один с темной, шероховатой поверхностью, а стенки другого будут светлыми и блестящими, и налить в них одинаковое количество кипящей воды, то быстрее остынет первый сосуд.

31.3. Законы Стефана — Больцмана и смещения Вина

Из закона Кирхгофа следует, что спектральная плотность энергетической светимости черного тела является универсальной функцией, поэтому нахождение ее явной зависимости от частоты и температуры является важной задачей теории теплового излучения.

Стефан, анализируя экспериментальные данные, и Больцман, применяя термодинамический метод, решили эту задачу лишь частично, установив зависимость энергетической светимости R_е от температуры. Согласно закону Стефана — Больцмана,

R_е = σ Т⁴, (31.9)

т. е. энергетическая светимость черного тела пропорциональна четвертей степени его термодинамической температуры; σ — постоянная Стефана — Больцмана: ее экспериментальное значение равно 5,67×10^-8 Вт/(м²×К⁴).

Закон Стефана — Больцмана, определяя зависимость R_е от температуры, не дает ответа относительно спектрального состава излучения черного тела. Из экспериментальных кривых зависимости функции r_λ,T от длины волны λ (r_λ,T = 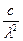´ ´ r_ν,T) при различных температурах (рис.30.2) Рис.31.2.

следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой зависимости r_λ,T от λ и осью абсцисс, пропорциональна энергетической светимости R_е черного тела и, следовательно, по закону Стефана — Больцмана, четвертей степени температуры.

В. Вин, опираясь на законы термо- и электродинамики, установил зависимость длины волны λ_max, соответствующей максимуму функции r_λ,T , от температуры Т. Согласно закону смещения Вина,

λ_max =b/Т, (31.10)

т. е. длина волны λ_max соответствующая максимальному значению спектральной
плотности энергетической светимости r_λ,T черного тела, обратно пропорциональна его термодинамической температуре. b — постоянная Вина ее экспериментальное значение равно 2,9×10^{-3 м}×К.

Выражение (31.10) называют законом смещения Вина, оно показывает смещение положения максимума функции r_λ,T по мере возрастания температуры в область коротких длин волн. Закон Вина объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (например, переход белого каления в красное при остывании металла).

Формулы Рэлея-Джинса и Планка

Из рассмотрения законов Стефана-Больцмана и Вина следует, что термодинамический подход к решению задачи о нахождении универсальной функции Кирхгофа не дал желаемых результатов.

Строгая попытка теоретического вывода зависимости r_λ,T принадлежит Рэлею и Джинсу, которые применили к тепловому излучению методы статистической физики, воспользовшим классическим законом равномерного распределения энергии по степеням свободы.

Формула Рэлея-Джинса для спектральной плотности энергетической светимости черного тела имеет вид:

r_ν,T = 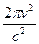<Е> = 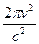kT, (31.11)

где <Е> = kT – средняя энергия осциллятора с собственной частотой ν.

Как показал опыт выражение (31.11) согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот эта формула расходится с экспериментом, а также с законом смещения Вина. И получить закон Стефана–Больцмана из этой формулы приводит к абсурду. Этот результат получил название «ультрафиолетовой катастрофы». Т.е. в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.

В области больших частот хорошее согласие с опытом дает формула Вина (закон излучения Вина):

r_ν,T =Сν³ А е ^–Аν/Т, (31.12)

где r_ν,T - спектральная плотность энергетической светимости черного тела, С и А – постоянные величины. В современных обозначениях с использованием

постоянной Планка закон излучения Вина может быть записан в виде

r_ν,T = 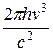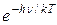. (31.13)

Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено Планком. Согласно выдвинутой квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями – квантами, причем энергия кванта пропорциональна частоте колебаний

Е₀ =hν = hс/λ,

где h=6,625×10^-34Дж×с – постоянная Планка.Так как излучение испускается порциями, то энергия осциллятора Е может принимать лишь определенные дискретные значения, кратные целому числу элементарных порций энергии Е₀

Е = nhν (n = 0,1,2…).

В данном случае среднюю энергию <Е> осциллятора нельзя принимать равной kT.

В приближении, что распределение осцилляторов по возможным дискретным состояниям подчиняется распределению Больцмана, средняя энергия осциллятора равна

<Е> =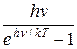 ,(31.14)

а спектральная плотность энергетической светимости определяется по формуле

r_ν,T = 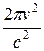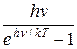.(31.15)

Планк вывел для универсальной функции Кирхгофа формулу

r_ν,T = 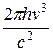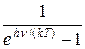, (31.16)

которая согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот и температур.

Из формулы Планка, зная универсальные постоянные h, k и с, можно вычислить постоянные Стефана-Больцмана σ и Вина b. И наоборот. Формула Планка хорошо согласуется с экспериментальными данными, но и содержит в себе частные законы теплового излучения, т.е. является полным решением задачи теплового излучения.

Оптическая пирометрия

Законы теплового излучения используются для измерения температуры раскаленных и самосветящихся тел (например, звезд). Методы измерения высоких температур, использующие зависимость спектральной плотности энергетической светимости или интегральной энергетической светимости тел от температуры, называются оптической пирометрией. Приборы для измерения температуры нагретых тел по интенсивности их теплового излучения в оптическом диапазоне спектра называются пирометрами. В зависимости от того, какой закон теплового излучения используется при измерении температуры тел, различают радиационную, цветовую и яркостную температуры.