Элементы квантовой механики

Основные формулы:

Уравнение Шредингера для стационарных состояний

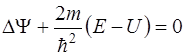, (3.1)

где Ψ – волновая функция, 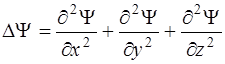, E – полная энергия частицы, U – ее потенциальная энергия, .

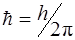Собственная волновая функция частицы, находящейся в бесконечно глубоком одномерном потенциальном ящике имеет вид

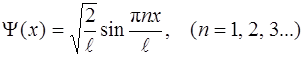(3.2)

где ℓ - ширина потенциального ящика.

Собственное значение энергии частицы, находящейся на n-ом энергетическом уровне в бесконечно глубоком одномерном потенциальном ящике определяется выражением

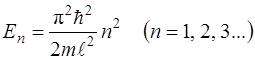(3.3)

Вероятность обнаружения частицы в интервале от x до x+dx выражается формулой

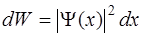, (3.4)

где │Ψ(x)│² – плотность вероятности.

Коэффициент прозрачности прямоугольного потенциального барьера конечной ширины рассчитывается по формуле

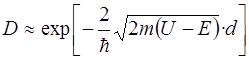, (3.5)

где U – высота потенциального барьера, d – ширина барьера.

Состояние электрона в атоме определяется квантовыми числами n, ℓ, m_ℓ, m_s. n – главное квантовое число, определяющее значение энергии атома; n=1, 2, 3… .

Собственные значения энергии электрона в атоме водорода

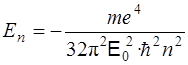(3.6)

ℓ - орбитальное квантовое число, определяющее значение орбитального момента импульса электрона; ℓ=1, 2…(n-1)

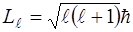(3.7)

m_ℓ - магнитное квантовое число, определяющее проекцию орбитального момента импульса электрона на направление внешнего магнитного поля; m_ℓ = -ℓ…0…+ℓ

L_H=m_ℓħ (3.8)

m_s - магнитное спиновое квантовое число, определяющее проекцию спина на направление внешнего магнитного поля; m_s = ±½

L_S,H=m_sħ (3.9)

Спин – собственный момент импульса электрона (и других элементарных частиц)

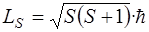(3.10)

где S – спиновое квантовое число; S=½.

Примеры решения задач

Задача 3.1. Электрон находится в одномерном бесконечно глубоком потенциальном ящике шириной l. Определить наименьшую разность двух соседних энергетических уровней (в эВ) электрона в двух случаях: 1) l=10 см; 2) l=1 нм. Сравнить полученные результаты. Показать на графике распределение плотности вероятности обнаружения электрона на данном уровне.

Решение.

Из формулы (3.3) для собственных значений энергии электрона при его движении в потенциальном ящике следует, что отношение энергии равно E₁: E₂: E₃:…=1:4:9: …, поэтому наименьшая разность уровней

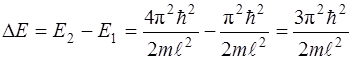
1) 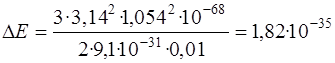(Дж) = 1,1·10^-16 эВ.

2) 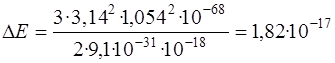(Дж) = 1,1 эВ.

Как видно из полученных результатов, в первом случае разность уровней столь мала, что дискретностью энергии можно пренебречь и считать, что в случае, когда электрон движется в ящике, размер которого много больше атомных размеров (~10^-10 м), его энергия изменяется непрерывно. Во втором случае электрон движется в потенциальном ящике, размер которого соизмерим с размерами атома. Значение ΔE получилось достаточно большим и дискретностью изменения энергии электрона пренебречь нельзя.

Ответ: 1) 1,1·10^-16 эВ; 2) (Дж) = 1,1эВ.

Задача 3.2. Электрон находится в бесконечно глубоком одномерном прямоугольном ящике шириной l. Определить: 1) вероятность того, что электрон находящийся в первом возбужденном состоянии, будет обнаружен в крайней левой четверти ящика; 2) вероятность нахождения электрона в середине ящика.

Решение.

Вероятность нахождения частицы в бесконечно узком интервале dx определяется формулой (3.4), следовательно, вероятность обнаружения частицы в левой четверти ящика, т.е. в интервале 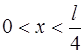, равна .

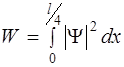Учитывая соотношение (3.2) и то, что первому возбужденному состоянию соответствует главное квантовое число n=2, получим

.

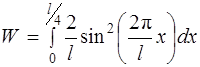Произведя замену 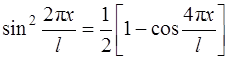и, разбив интеграл на два, перейдем к выражению

,

.

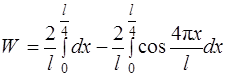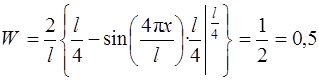Нетрудно показать, что вероятность обнаружения электрона в правой крайней четверти ящика тоже равна 0,5.

Рис. 3.1

Для ответа на второй вопрос достаточно определить плотность вероятности обнаружения частицы в точке

.

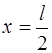
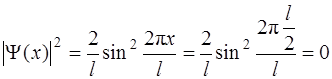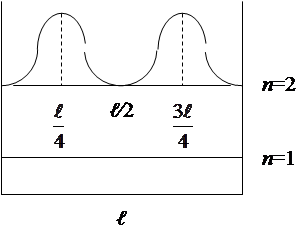
Распределение плотности вероятности обнаружения электрона на втором уровне приведено на рис. 3.1.

Задача 3.3. Электрон с энергией 3,6 эВ движется в положительном направлении оси x, встречая на своем пути потенциальный барьер. Чему равна высота барьера (в эВ), если вероятность прохождения через него электрона равна 0,2, а ширина барьера 0,5 нм?

Решение.

Вероятность W прохождения частицы сквозь потенциальный барьер по физическому смыслу совпадает с коэффициентом прозрачности D, поэтому может быть определена по формуле (3.5)

,

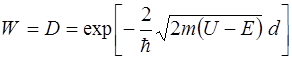где U – искомая высота потенциального барьера.

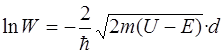
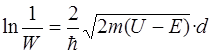
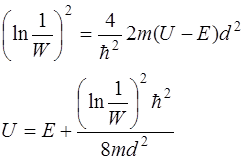
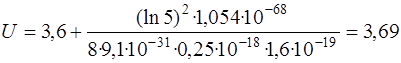(эВ).

Ответ: U=3,6 эВ.

Задача 3.4. Определить возможные значения орбитального момента импульса электрона в возбужденном атоме водорода, если энергия возбуждения 12,09 эВ.

Решение.

Орбитальный момент импульса электрона определяется квантовым числом ℓ по формуле (3.7). Так как ряд возможных значений ℓ ограничен величиной (n-1), найдем главное квантовое число n с помощью формулы

E =hν=E_n-E₁; E =hcR .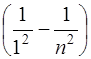

Учитывая, что hcR= E _i=13,6 эВ, получим 12,09=13,6 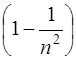, откуда 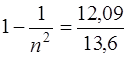и n=3, следовательно, ℓ=0, 1, 2.

Используя формулу (3.7), получим:

при ℓ=0 L_ℓ=0;

при ℓ=1 L_ℓ= 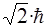=1,49·10^-34 Дж·с;

при ℓ=2 L_ℓ= 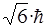=2,6·10^-34 Дж·с.

Ответ: 0; 1,49·10^-34 Дж·с; 2,6·10^-34 Дж·с.

Задача 3.5. Определить наименьший угол, который может образовать вектор орбитального момента импульса электрона в атоме с направлением внешнего магнитного поля. Электрон в атоме находится в d-состоянии.

Решение.

d-состоянию электрона соответствует значение орбитального квантового числа ℓ=2, следовательно, магнитное квантовое число m_ℓ, определяющее проекцию орбитального момента импульса электрона на направление магнитного поля, может принимать значения: -2, -1, 0, +1, +2.

Орбитальный момент импульса равен (3.7)

.

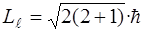Этот вектор занимает в магнитном поле такое положение, что его проекции на направление этого поля равны (3.8):

L_H = –2ħ, –1ħ, 0, +1ħ, +2ħ.

На рис. 3.2 представлены возможные ориентации вектора орбитального момента импульса электрона во внешнем магнитном поле. 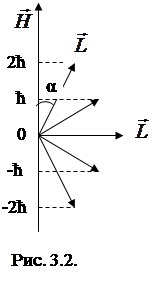Из рисунка видно, что для наименьшего угла α

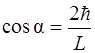
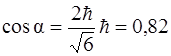
α=35˚10′.

Ответ: α=35˚10′.