Насыщенный пар, кипение, влажность воздуха
Насыщенный пар. 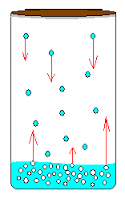 Если сосуд с жидкостью плотно закрыть, то сначала количество жидкости уменьшится, а затем будет оставаться постоянным. При неизменной температуре система жидкость - пар придет в состояние теплового равновесия и будет находиться в нем сколь угодно долго. Одновременно с процессом испарения происходит и конденсация, оба процесса в среднем компенсируют друг друга. В первый момент, после того как жидкость нальют в сосуд и закроют его, жидкость будетиспаряться и плотность пара над ней будет увеличиваться. Однако одновременно с этим будет расти и число молекул, возвращающихся в жидкость. Чем больше плотность пара, тем большее число его молекул возвращается в жидкость. В результате в закрытом сосуде при постоянной температуре установится динамическое (подвижное) равновесие между жидкостью и паром, т. е. число молекул, покидающих поверхность жидкости за некоторый промежуток времени, будет равно в среднем числу молекул пара, возвратившихся за то же время в жидкость. Пар, находящийся в динамическом равновесии со своей жидкостью, называют насыщенным паром. Это определение подчеркивает, что в данном объеме при данной температуре не может находиться большее количество пара. Более подробно здесь Давление насыщенного пара. Что будет происходить с насыщенным паром, если уменьшить занимаемый им объем? Например, если сжимать пар, находящийся в равновесии с жидкостью в цилиндре под поршнем, поддерживая температуру содержимого цилиндра постоянной. При сжатии пара равновесие начнет нарушаться. Плотность пара в первый момент немного увеличится, и из газа в жидкость начнет переходить большее число молекул, чем из жидкости в газ. Ведь число молекул, покидающих жидкость в единицу времени, зависит только от температуры, и сжатие пара это число не меняет. Процесс продолжается до тех пор, пока вновь не установится динамическое равновесие и плотность пара, а значит, и концентрация его молекул не примут прежних своих значений. Следовательно, концентрация молекул насыщенного пара при постоянной температуре не зависит от его объема. Так как давление пропорционально концентрации молекул (p=nkT), то из этого определения следует, что давление насыщенного пара не зависит от занимаемого им объема. Давление pн.п. пара, при котором жидкость находится в равновесии со своим паром, называют давлением насыщенного пара. Зависимость давления насыщенного пара от температуры. Если сосуд с жидкостью плотно закрыть, то сначала количество жидкости уменьшится, а затем будет оставаться постоянным. При неизменной температуре система жидкость - пар придет в состояние теплового равновесия и будет находиться в нем сколь угодно долго. Одновременно с процессом испарения происходит и конденсация, оба процесса в среднем компенсируют друг друга. В первый момент, после того как жидкость нальют в сосуд и закроют его, жидкость будетиспаряться и плотность пара над ней будет увеличиваться. Однако одновременно с этим будет расти и число молекул, возвращающихся в жидкость. Чем больше плотность пара, тем большее число его молекул возвращается в жидкость. В результате в закрытом сосуде при постоянной температуре установится динамическое (подвижное) равновесие между жидкостью и паром, т. е. число молекул, покидающих поверхность жидкости за некоторый промежуток времени, будет равно в среднем числу молекул пара, возвратившихся за то же время в жидкость. Пар, находящийся в динамическом равновесии со своей жидкостью, называют насыщенным паром. Это определение подчеркивает, что в данном объеме при данной температуре не может находиться большее количество пара. Более подробно здесь Давление насыщенного пара. Что будет происходить с насыщенным паром, если уменьшить занимаемый им объем? Например, если сжимать пар, находящийся в равновесии с жидкостью в цилиндре под поршнем, поддерживая температуру содержимого цилиндра постоянной. При сжатии пара равновесие начнет нарушаться. Плотность пара в первый момент немного увеличится, и из газа в жидкость начнет переходить большее число молекул, чем из жидкости в газ. Ведь число молекул, покидающих жидкость в единицу времени, зависит только от температуры, и сжатие пара это число не меняет. Процесс продолжается до тех пор, пока вновь не установится динамическое равновесие и плотность пара, а значит, и концентрация его молекул не примут прежних своих значений. Следовательно, концентрация молекул насыщенного пара при постоянной температуре не зависит от его объема. Так как давление пропорционально концентрации молекул (p=nkT), то из этого определения следует, что давление насыщенного пара не зависит от занимаемого им объема. Давление pн.п. пара, при котором жидкость находится в равновесии со своим паром, называют давлением насыщенного пара. Зависимость давления насыщенного пара от температуры. 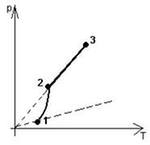 Состояние насыщенного пара, как показывает опыт, приближенно описывается уравнением состояния идеального газа, а его давление определяется формулой Р = nкТ С ростом температуры давление растет. Так как давление насыщенного пара не зависит от объема, то, следовательно, оно зависит только от температуры. Однако зависимость рн.п. от Т, найденная экспериментально, не является прямо пропорциональной, как у идеального газа при постоянном объеме. С увеличением температуры давление реального насыщенного пара растет быстрее, чем давление идеального газа (рис. участок кривой 12). Почему это происходит? При нагревании жидкости в закрытом сосуде часть жидкости превращается в пар. В результате согласно формуле Р = nкТ давление насыщенного пара растет не только вследствие повышения температуры жидкости, но и вследствие увеличения концентрации молекул (плотности) пара. В основном увеличение давления при повышении температуры определяется именно увеличением концентрации. (Главное различие в поведении идеального газа и насыщенного пара состоит в том, что при изменении температуры пара в закрытом сосуде (или при изменении объема при постоянной температуре) меняется масса пара. Жидкость частично превращается в пар, или, напротив, пар частично конденсируется. С идеальным газом ничего подобного не происходит.). Когда вся жидкость испарится, пар при дальнейшем нагревании перестанет быть насыщенным и его давление при постоянном объеме будет возрастать прямо пропорционально абсолютной температуре (см. рис., участок кривой 23). Кипение. Кипение – это интенсивный переход вещества из жидкого состояния в газообразное, происходящее по всему объему жидкости (а не только с ее поверхности). (Конденсация – обратный процесс.) По мере увеличения температуры жидкости интенсивность испарения увеличивается. Наконец, жидкость начинает кипеть. При кипении по всему объему жидкости образуются быстро растущие пузырьки пара, которые всплывают на поверхность. Температура кипения жидкости остается постоянной. Это происходит потому, что вся подводимая к жидкости энергия расходуется на превращение ее в пар. При каких условиях начинается кипение? Состояние насыщенного пара, как показывает опыт, приближенно описывается уравнением состояния идеального газа, а его давление определяется формулой Р = nкТ С ростом температуры давление растет. Так как давление насыщенного пара не зависит от объема, то, следовательно, оно зависит только от температуры. Однако зависимость рн.п. от Т, найденная экспериментально, не является прямо пропорциональной, как у идеального газа при постоянном объеме. С увеличением температуры давление реального насыщенного пара растет быстрее, чем давление идеального газа (рис. участок кривой 12). Почему это происходит? При нагревании жидкости в закрытом сосуде часть жидкости превращается в пар. В результате согласно формуле Р = nкТ давление насыщенного пара растет не только вследствие повышения температуры жидкости, но и вследствие увеличения концентрации молекул (плотности) пара. В основном увеличение давления при повышении температуры определяется именно увеличением концентрации. (Главное различие в поведении идеального газа и насыщенного пара состоит в том, что при изменении температуры пара в закрытом сосуде (или при изменении объема при постоянной температуре) меняется масса пара. Жидкость частично превращается в пар, или, напротив, пар частично конденсируется. С идеальным газом ничего подобного не происходит.). Когда вся жидкость испарится, пар при дальнейшем нагревании перестанет быть насыщенным и его давление при постоянном объеме будет возрастать прямо пропорционально абсолютной температуре (см. рис., участок кривой 23). Кипение. Кипение – это интенсивный переход вещества из жидкого состояния в газообразное, происходящее по всему объему жидкости (а не только с ее поверхности). (Конденсация – обратный процесс.) По мере увеличения температуры жидкости интенсивность испарения увеличивается. Наконец, жидкость начинает кипеть. При кипении по всему объему жидкости образуются быстро растущие пузырьки пара, которые всплывают на поверхность. Температура кипения жидкости остается постоянной. Это происходит потому, что вся подводимая к жидкости энергия расходуется на превращение ее в пар. При каких условиях начинается кипение? 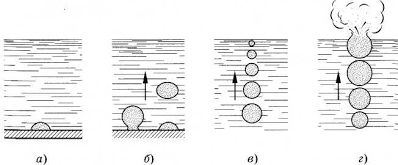 В жидкости всегда присутствуют растворенные газы, выделяющиеся на дне и стенках сосуда, а также на взвешенных в жидкости пылинках, которые являются центрами парообразования. Пары жидкости, находящиеся внутри пузырьков, являются насыщенными. С увеличением температуры давление насыщенных паров возрастает и пузырьки увеличиваются в размерах. Под действием выталкивающей силы они всплывают вверх. Если верхние слои жидкости имеют более низкую температуру, то в этих слоях происходит конденсация пара в пузырьках. Давление стремительно падает, и пузырьки захлопываются. Захлопывание происходит настолько быстро, что стенки пузырька, сталкиваясь, производят нечто вроде взрыва. Множество таких микровзрывов создает характерный шум. Когда жидкость достаточно прогреется, пузырьки перестанут захлопываться и всплывут на поверхность. Жидкость закипит. Понаблюдайте внимательно за чайником на плите. Вы обнаружите, что перед закипанием он почти перестает шуметь. Зависимость давления насыщенного пара от температуры объясняет, почему температура кипения жидкости зависит от давления на ее поверхность. Пузырек пара может расти, когда давление насыщенного пара внутри него немного превосходит давление в жидкости, которое складывается из давления воздуха на поверхность жидкости (внешнее давление) и гидростатического давления столба жидкости . Кипение начинается при температуре, при которой давление насыщенного пара в пузырьках сравнивается с давлением в жидкости. Чем больше внешнее давление, тем выше температура кипения. И наоборот, уменьшая внешнее давление, мы тем самым понижаем температуру кипения. Откачивая насосом воздух и пары воды из колбы, можно заставить воду кипеть при комнатной температуре. У каждой жидкости своя температура кипения (которая остается постоянной, пока вся жидкость не выкипит), которая зависит от давления ее насыщенного пара. Чем выше давление насыщенного пара, тем ниже температура кипения жидкости. Заполни опорный конспект Контрольные вопросы Влажность воздуха и ее измерение. В окружающем нас воздухе практически всегда находится некоторое количество водяных паров. Влажность воздуха зависит от количества водяного пара, содержащегося в нем. Сырой воздух содержит больший процент молекул воды, чем сухой. Большое значение имеет относительная влажность воздуха, сообщения о которой каждый день звучат в сводках метеопрогноза. В жидкости всегда присутствуют растворенные газы, выделяющиеся на дне и стенках сосуда, а также на взвешенных в жидкости пылинках, которые являются центрами парообразования. Пары жидкости, находящиеся внутри пузырьков, являются насыщенными. С увеличением температуры давление насыщенных паров возрастает и пузырьки увеличиваются в размерах. Под действием выталкивающей силы они всплывают вверх. Если верхние слои жидкости имеют более низкую температуру, то в этих слоях происходит конденсация пара в пузырьках. Давление стремительно падает, и пузырьки захлопываются. Захлопывание происходит настолько быстро, что стенки пузырька, сталкиваясь, производят нечто вроде взрыва. Множество таких микровзрывов создает характерный шум. Когда жидкость достаточно прогреется, пузырьки перестанут захлопываться и всплывут на поверхность. Жидкость закипит. Понаблюдайте внимательно за чайником на плите. Вы обнаружите, что перед закипанием он почти перестает шуметь. Зависимость давления насыщенного пара от температуры объясняет, почему температура кипения жидкости зависит от давления на ее поверхность. Пузырек пара может расти, когда давление насыщенного пара внутри него немного превосходит давление в жидкости, которое складывается из давления воздуха на поверхность жидкости (внешнее давление) и гидростатического давления столба жидкости . Кипение начинается при температуре, при которой давление насыщенного пара в пузырьках сравнивается с давлением в жидкости. Чем больше внешнее давление, тем выше температура кипения. И наоборот, уменьшая внешнее давление, мы тем самым понижаем температуру кипения. Откачивая насосом воздух и пары воды из колбы, можно заставить воду кипеть при комнатной температуре. У каждой жидкости своя температура кипения (которая остается постоянной, пока вся жидкость не выкипит), которая зависит от давления ее насыщенного пара. Чем выше давление насыщенного пара, тем ниже температура кипения жидкости. Заполни опорный конспект Контрольные вопросы Влажность воздуха и ее измерение. В окружающем нас воздухе практически всегда находится некоторое количество водяных паров. Влажность воздуха зависит от количества водяного пара, содержащегося в нем. Сырой воздух содержит больший процент молекул воды, чем сухой. Большое значение имеет относительная влажность воздуха, сообщения о которой каждый день звучат в сводках метеопрогноза. 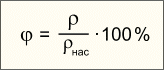 Относительная влажность — это отношение плотности водяного пара, содержащегося в воздухе, к плотности насыщенного пара при данной температуре, выраженное в процентах (показывает, насколько водяной пар в воздухе близок к насыщению). Относительная влажность — это отношение плотности водяного пара, содержащегося в воздухе, к плотности насыщенного пара при данной температуре, выраженное в процентах (показывает, насколько водяной пар в воздухе близок к насыщению).  Точка росы Сухость или влажность воздуха зависит от того, насколько близок его водяной пар к насыщению. Если влажный воздух охлаждать, то находящийся в нем пар можно довести до насыщения, и далее он будет конденсироваться. Признаком того, что пар насытился является появление первых капель сконденсировавшейся жидкости - росы. Температура, при которой пар, находящийся в воздухе, становится насыщенным, называется точкой росы. Точка росы также характеризует влажность воздуха. Примеры: выпадение росы под утро, запотевание холодного стекла, если на него подышать, образование капли воды на холодной водопроводной трубе, сырость в подвалах домов. Для измерения влажности воздуха используют измерительные приборы - гигрометры. Существуют несколько видов гигрометров, но основные: волосной и психрометрический. Точка росы Сухость или влажность воздуха зависит от того, насколько близок его водяной пар к насыщению. Если влажный воздух охлаждать, то находящийся в нем пар можно довести до насыщения, и далее он будет конденсироваться. Признаком того, что пар насытился является появление первых капель сконденсировавшейся жидкости - росы. Температура, при которой пар, находящийся в воздухе, становится насыщенным, называется точкой росы. Точка росы также характеризует влажность воздуха. Примеры: выпадение росы под утро, запотевание холодного стекла, если на него подышать, образование капли воды на холодной водопроводной трубе, сырость в подвалах домов. Для измерения влажности воздуха используют измерительные приборы - гигрометры. Существуют несколько видов гигрометров, но основные: волосной и психрометрический. 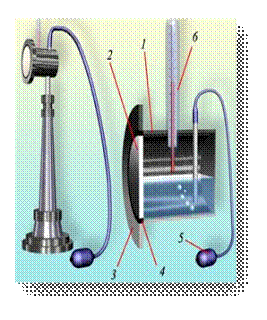 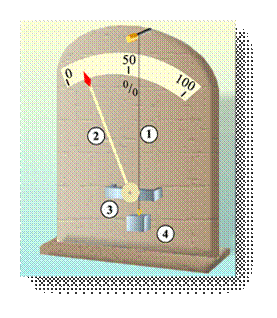  Так как непосредственно измерить давление водяных паров в воздухе сложно, относительную влажность воздуха измеряют косвенным путем. Известно, что от относительной влажности воздуха зависит скорость испарения. Чем меньше влажность воздуха, тем легче влаге испаряться. В психрометре есть два термометра. Один - обычный, его называют сухим. Он измеряет температуру окружающего воздуха. Колба другого термометра обмотана тканевым фитилем и опущена в емкость с водой. Второй термометр показывает не температуру воздуха, а температуру влажного фитиля, отсюда и название увлажненный термометр. Чем меньше влажность воздуха, тем интенсивнее испаряется влага из фитиля, тем большее количество теплоты в единицу времени отводится от увлажненного термометра, тем меньше его показания, следовательно, тем больше разность показаний сухого и увлажненного термометров. Определив разность показаний сухого и увлажненного термометров, по специальной таблице, расположенной на психрометре, находят значение относительной влажности. Так как непосредственно измерить давление водяных паров в воздухе сложно, относительную влажность воздуха измеряют косвенным путем. Известно, что от относительной влажности воздуха зависит скорость испарения. Чем меньше влажность воздуха, тем легче влаге испаряться. В психрометре есть два термометра. Один - обычный, его называют сухим. Он измеряет температуру окружающего воздуха. Колба другого термометра обмотана тканевым фитилем и опущена в емкость с водой. Второй термометр показывает не температуру воздуха, а температуру влажного фитиля, отсюда и название увлажненный термометр. Чем меньше влажность воздуха, тем интенсивнее испаряется влага из фитиля, тем большее количество теплоты в единицу времени отводится от увлажненного термометра, тем меньше его показания, следовательно, тем больше разность показаний сухого и увлажненного термометров. Определив разность показаний сухого и увлажненного термометров, по специальной таблице, расположенной на психрометре, находят значение относительной влажности. |
Вопрос 2
временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механикаНьютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.
Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, — релятивистскими скоростями. Основным отличием СТО от классической механики является зависимость (наблюдаемых) пространственных и временных характеристик от скорости.
Центральное место в специальной теории относительности занимают преобразования Лоренца, которые позволяют преобразовывать пространственно-временные координаты событий при переходе от одной инерциальной системы отсчета к другой.
Специальная теория относительности была создана Альбертом Эйнштейном в работе 1905 года «К электродинамике движущихся тел». Математический аппарат преобразований координат и времени между различными системами отсчета (с целью сохранения уравнений электромагнитного поля), был ранее сформулирован французским математиком А. Пуанкаре (который и предложил их назвать «преобразованиями Лоренца» — сам Лоренц вывел до этого только приближённые формулы[1]). А. Пуанкаре также первым показал, что эти преобразования можно интерпретировать как повороты в четырехмерном пространстве-времени с мнимым временем (опередив Г. Минковского) и показал, что преобразования Лоренца образуют группу. О роли А. Пуанкаре в создании теории относительности см. подробнее: Пуанкаре, Анри#Роль Пуанкаре в создании теории относительности.
Непосредственно термин «теория относительности» был предложен М. Планком. В дальнейшем, после разработки А. Эйнштейном теории гравитации — общей теории относительности — к первоначальной теории начал применяться термин «специальная» или «частная» теория относительности.
Билет 10 Вопрос 1





Поверхностное натяжение, смачивание, капиллярные явления Молекула жидкости, находящаяся внутри жидкости, взаимодействует с окружающими её молекулами. Такое взаимодействие симметрично и равнодействующая их равна нулю. Для молекулы, находящейся вблизи поверхности, симметрия нарушается и возникает сила некомпенсированная другими молекулами, направленная внутрь жидкости. При этом потенциальная энергия для молекул, находящихся на поверхности пропорциональна её площади. Поверхностное натяжение σ (коэффициент) представляет собой отношение изменения свободной поверхностной энергии жидкости, отнесенной к изменению единицы площади поверхностного слоя: σ = ΔЕ/Δω, Дж/м2 или сила поверхностного натяжения, отнесенная к единице длины на свободной поверхности: Условием устойчивого равновесия жидкостей является минимум свободной энергии жидкости. В условиях отсутствия внешних сил и заданного объема, жидкость стремится принять минимальную площадь поверхности – сферическую форму. На границе соприкосновения трех фаз: жидкость, газ, твердое тело наблюдается явление называемое смачиванием, заключающее в возникновении искривления свободной поверхности жидкости и возникновения мениска. Мерой смачивания является величина cos Θ, где Θ – краевой угол смачивания между смоченной поверхностью твердого тела и мениском в точках их пересечения - периметра смачивания жидкость имеет вогнутый мениск и смачивает твердое тело – гидрофильные поверхности. При Θ > π/2 мениск жидкости выпуклый – гидрофобные поверхности. При Θ → 0 мениск касателенк поверхности тела, условие идеального смачивания. Рис.1.4. Пример гидрофобной и гидрофильной поверхностей На рис.1.5 показано взаиморасположение коэффициентов поверхностного натяжения σ на границах раздела фаз: твердая поверхность – жидкость – газ. Рис.1.5 Жидкость (2) на границе раздела фаз: 1- твердое тело, 3 – газовая среда. Взаиморасположение коэффициентов поверхностного натяжения. Величина дополнительного давления за счет искривления поверхностного слоя при средней кривизне поверхности (закон Лапласа - зависимость перепада гидростатического давления Δp на поверхности раздела двух фаз: жидкость — жидкость, жидкость — газ или пар от межфазного поверхностного натяжения σ и средней кривизны поверхности в рассматриваемой точке): (1.26) где 2σ –удвоенный коэффициент поверхностного натяжения (для газовых пузырей в жидкостях, мыльных пузырей), 1/R1 и 1/R2 –кривизна двух взаимно перпендикулярных, нормальных сечений поверхности в данной точке (подробнее о понятиях: кривизна поверх-ности и радиус кривизны см. Приложение В); Δр = р1-р2 , где р1 – давление с вогнутой стороны поверхности, р2 – давление с выпуклой стороны поверхности. Применение закона Лапласа к поверхности раздела вода — пар в капилляре: Δр = р1 - p2; R1 и R2 — радиусы кривизны в точке О во-гнутой поверхности (R1 = ОА и R2 = ОВ) определяются в двух взаим-но перпендикулярных сечениях ACD и BEF (рис.1.6). Рис.1.6 К определению радиуса кривизны поверхности мениска воды в капилляре Величина избыточного давления для сферических менисков: Δр =2σ/R (1.27) Для цилиндрических менисков: Δр =σ/R (1.28) Капиллярность – свойство жидкости изменять положение её поверхности, вызванное натяжением и силой взаимодействия между нею и стенками узких цилиндрических трубок (1-2 мм в диаметре) или мелкими порами грунта. Капиллярность зависит от температуры, уменьшаясь с ее ростом (рис.1.7). Рис.1.7 Поднятие воды в капилляре Если сближать плоские стенки сосуда таким образом, чтобы зоны искривления начали перекрываться, то образуется вогнутый мениск — полностью искривленная поверхность. В жидкости под мениском капиллярное давление отрицательно, под его действием жид-кость всасывается в щель до тех пор, пока вес столба жидкости (высотой h) не уравновесит действующее капиллярное давление Δp. В со-стоянии равновесия: (ρ1 —ρ2) gh = Δp = 2σ12/r, (1.29) где ρ1 и ρ2 — плотности жидкости 1 и газа 2. Это выражение, известно как формула Д. Жюрена (J. Jurin, 1684—1750), определяет высоту капиллярного поднятия жидкости h, полностью смачивающей стенки капилляра. Жидкость, не смачивающая поверхность, образует выпуклый мениск, что вызывает сё опускание в капилляре ниже уровня свободной поверхности Высота поднятия (смачивающей) или опускания (не смачиваю-щей) жидкости в капилляре, диаметром d, равна (формула Жюрена): (1.30) Вода из всех жидкостей имеет наибольшее значение поверхностное натяжение σ = 0,0726 Н/м. Для воды при температуре 20 0С в трубке диаметром d мм высота капиллярного поднятия выражается формулой: h=30/d, мм.
Вопрос 2
Материал из Википедии — свободной энциклопедии
Эта статья включает описание термина «энергия покоя»
Эта статья включает описание термина «E=mc2»; см. также другие значения.

Формула на небоскрёбе Тайбэй 101 во время одного из мероприятий Всемирного года физики (2005)
Эквивале́нтность ма́ссы и эне́ргии — физическая концепция теории относительности, согласно которой полная энергия физического объекта (физической системы, тела) равна его (её) массе, умноженной на размерный множитель квадрата скорости света в вакууме:
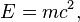 где
где 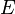 — энергия объекта,
— энергия объекта, 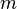 — его масса,
— его масса,  — скорость света в вакууме, равная 299 792 458 м/с.
— скорость света в вакууме, равная 299 792 458 м/с.
В зависимости от того, что понимается под терминами «масса» и «энергия», данная концепция может быть интерпретирована двояко:
· с одной стороны, концепция означает, что масса тела (инвариантная масса, называемая также массой покоя)[1] равна (с точностью до постоянного множителя c²)[2]энергии, «заключённой в нём», то есть его энергии, измеренной или вычисленной в сопутствующей системе отсчёта (системе отсчёта покоя), так называемой энергии покоя, или в широком смысле внутренней энергии этого тела[3],
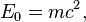 где
где 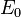 — энергия покоя тела,
— энергия покоя тела, 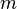 — его масса покоя;
— его масса покоя;
· с другой стороны, можно утверждать, что любому виду энергии (не обязательно внутренней) физического объекта (не обязательно тела) соответствует некая масса; например, для любого движущегося объекта было введено понятие релятивистской массы, равной (с точностью до множителя c²) полной энергии этого объекта (включаякинетическую)[4],
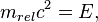 где
где 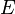 — полная энергия объекта,
— полная энергия объекта, 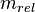 — его релятивистская масса.
— его релятивистская масса.
Первая интерпретация не является лишь частным случаем второй. Хотя энергия покоя является частным случаем энергии, а 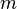 практически равна
практически равна 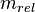 в случае нулевой или малой скорости движения тела, но
в случае нулевой или малой скорости движения тела, но 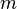 имеет выходящее за рамки второй интерпретации физическое содержание: эта величина является скалярным (то есть выражаемым одним числом) инвариантным (неизменным при смене системы отсчёта) множителем в определении 4-вектора энергии-импульса, аналогичным ньютоновской массе и являющимся её прямым обобщением[5], и к тому же
имеет выходящее за рамки второй интерпретации физическое содержание: эта величина является скалярным (то есть выражаемым одним числом) инвариантным (неизменным при смене системы отсчёта) множителем в определении 4-вектора энергии-импульса, аналогичным ньютоновской массе и являющимся её прямым обобщением[5], и к тому же  является модулем 4-импульса. Дополнительно, именно
является модулем 4-импульса. Дополнительно, именно  (а не
(а не 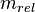 ) является единственным скаляром, который не только характеризует инертные свойства тела при малых скоростях, но и через который эти свойства могут быть достаточно просто записаны для любой скорости движения тела[6].
) является единственным скаляром, который не только характеризует инертные свойства тела при малых скоростях, но и через который эти свойства могут быть достаточно просто записаны для любой скорости движения тела[6].
И таким образом, 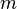 — инвариантная масса — физическая величина, имеющая самостоятельное и во многом более фундаментальное значение[7].
— инвариантная масса — физическая величина, имеющая самостоятельное и во многом более фундаментальное значение[7].
В современной теоретической физике концепцию эквивалентности массы и энергии обычно используется в первом смысле[8]. Главной причиной, почему приписывание массы любому виду энергии считается чисто терминологически неудачным и поэтому практически вышло из употребления в стандартной научной терминологии, является следующая из этого полная синонимичность понятий массы и энергии. Кроме того, неаккуратное использование такого подхода может запутывать[9] и в конечном итоге оказывается неоправданным. Таким образом, в настоящее время термин «релятивистская масса» в профессиональной литературе практически не встречается, а когда говорится о массе, имеется в виду инвариантная масса. В то же время термин «релятивистская масса» используется для качественных рассуждений в прикладных вопросах, а также в образовательном процессе и в научно-популярной литературе. Этот термин подчёркивает увеличение инертных свойств движущегося тела вместе с его энергией, что само по себе вполне содержательно[10].
В наиболее универсальной форме принцип был сформулирован впервые Альбертом Эйнштейном в 1905 году, однако представления о связи энергии и инертных свойств тела развивались и в более ранних работах других исследователей.
В современной культуре формула 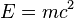 является едва ли не самой известной из всех физических формул, что обуславливается её связью с устрашающей мощьюатомного оружия. Кроме того, именно эта формула является символом теории относительности и широко используется популяризаторами науки[11].
является едва ли не самой известной из всех физических формул, что обуславливается её связью с устрашающей мощьюатомного оружия. Кроме того, именно эта формула является символом теории относительности и широко используется популяризаторами науки[11].
