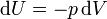Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами

Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила названиевечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.

Применим первый закон термодинамики к изопроцессам в газах.

1. Визохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно,

Q = ΔU = U (T2) – U (T1).

2. Здесь U (T₁) и U (T₂) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).

3. В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением

A = p (V2 – V1) = p ΔV.

4. Первый закон термодинамики для изобарного процесса дает:

Q = U (T2) – U (T1) + p (V2 – V1) = ΔU + p ΔV.

5. При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T₂ < T₁; внутренняя энергия убывает, ΔU < 0.

6. В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.

Первый закон термодинамики для изотермического процесса выражается соотношением

Q = A.

№9
Изотермический процесс (T = const,следовательноΔU = 0).
По первому закону термодинамики: Q = A'.
Газ совершает работу A' за счет подводимого тепла Q (A'>0, Q>0).
Совершение работы внешними силами A (сжатие газа) требует отвода тепла Q от газа для сохранения его температуры (A>0, Q<0).

Изохорный процесс (V = const,следовательно A = 0).
По первому закону термодинамики:ΔU = Q.
Нагревание газа в закрытом сосуде приводит к увеличению его внутренней энергии U (температуры) (Q>0, ΔU>0).
Охлаждение газа в закрытом сосуде приводит к уменьшению его внутренней энергии U (температуры) (Q<0, ΔU<0).

Изобарный процесс (p = const).
По первому закону термодинамики:Q = ΔU + A'.
Подводимое к газу тепло Q частично идет на увеличение внутренней энергии U, а частично на совершение работы газом A' (Q>0, ΔU>0, A'>0).
Работа внешних сил A при изобарном сжатии газа требует отвода тепла Q от газа, одновременно уменьшается его внутренняя энергия U (Q<0, ΔU<0, A>0).

Адиабатный процесс - процесс, протекающий без теплообмена с окружающей средой (Q = 0).
По первому закону термодинамики: ΔU = A.
Вся работа внешних сил А идет только на увеличение внутренней энергии газа (A>0, ΔU>0).
Работа газа А' совершается только за счет потери внутренней энергии газа (A'>0, ΔU<0).

Полезные формулы:

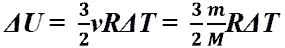Изменение внутренней энергии
идеального одноатомного газа.

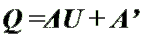Количество теплоты, переданное телу,
идет на изменение его внутренней энергии
и на совершение им работы (Первый закон термодинамики).
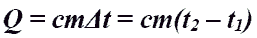Количество теплоты при нагревании и охлаждении газа.

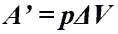Работа газа при изобарном процессе (p = const)
№10
Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло.

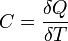
Адиабатический

В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть 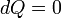. Однако, объём, давление и температура меняются, то есть .

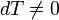Следовательно, теплоемкость идеального газа в адиабатическом процессе равна нулю: .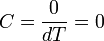

[править]Изотермический

В изотермическом процессе постоянна температура, то есть 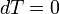. При изменении объема газу передается (или отбирается) некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к бесконечности: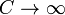

[править]Изохорный

В изохорическом процессе постоянен объем, то есть 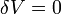. Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение ( 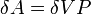). Первое Начало Термодинамики для изохорического процесса имеет вид:

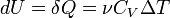
А для идеального газа

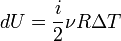
Таким образом,

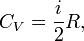
где 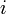— число степеней свободы частиц газа.

[править]Изобарный

В изобарном процессе ( ):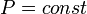

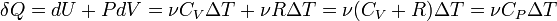
C_P=δQ/νΔT=C_V+R=((i+2)/2)*R

№12
Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством . Серьёзное исследование адиабатических процессов началось в XVIII веке^[1].
Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии^[5], то адиабатический процесс в силу отсутствия теплообмена ( 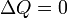) системы со средой сводится только к последним двум процессам^[6]. Поэтому, первое начало термодинамики в этом случае приобретает вид^{[7][Комм 1]}

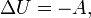
где 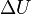— изменение внутренней энергии тела, 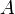— работа, совершаемая системой.

Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит^[8]:

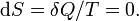
Здесь 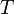— температура системы, 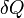— теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла^[8].

[править]Работа газа

Совершение над газом работы на элементарном участке dh. Совершаемая работа показана красными лампочками

Поясним понятие работы применительно к адиабатическому процессу. В частном случае, когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем, если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок 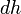совершать работу^[9][10]

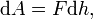
где F — сила, с которой газ действует на поршень. Перепишем уравнение:

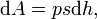
где s — площадь поршня. Тогда работа будет равна^[9][10]

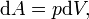
где 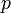— давление газа, 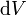— малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения. Данное уравнение справедливо и при расширении на произвольных объёмах. Для этого достаточно разбить поверхность расширения на элементарные участки 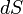на которых расширение одинаково^[9].

Основное уравнение термодинамики примет вид^[11]:

(1)

Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает

• электростатическое поле,
• стационарное поле температуры,
• поле давления,
• поле потенциала скорости в гидродинамике.

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид: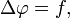

где 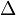— оператор Лапласа или лапласиан, а 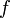— вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

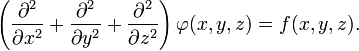
В декартовой системе координат оператор Лапласа записывается в форме 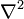и уравнение Пуассона принимает вид:

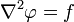
Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):

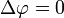
Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод»

№13
. Работа газа при адиабатном процессе равна убыли внутренней энергии:
.
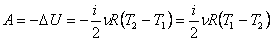№14
Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.
КПД тепловой машины Карно

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.

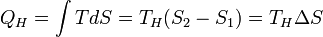Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

.

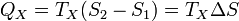Отсюда коэффициент полезного действия тепловой машины Карно равен

.

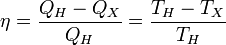Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равнаабсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Например, КПД идеального цикла Стирлинга равен КПД цикла Карно.

№15
Второй закон термодинамики. Энтропия.