Принцип действия циклических ускорителей заряженных частиц
МАГНИТНОЕ ПОЛЕ
Изучение магнитных явлений развивалось совершенно отдельно от исследований электричества. Казалось, что магнитные явления свойственны в первую очередь железу и каким-то образом самой Земле. Магниты могут, как притягиваться, так и отталкиваться друг от друга. При изучении взаимодействия постоянных магнитов было установлено: постоянные магниты имеют два полюса: северный и южный; одноименные полюсы отталкиваются друг от друга, а разноименные притягиваются. Взаимодействие между магнитами осуществляется посредством их магнитных полей. Магнитное поле проявляется в действии на магнитную стрелку, на рамку с током, на движущийся заряд. На рамку с током и на магнитную стрелку магнитное поле оказывает ориентирующее действие. Северным полюсом магнитной стрелки (магнита) называют полюс конца стрелки в поле Земли, обращенный к Северу Земли, а южным полюс конца стрелки, обращенный к югу Земли. Сориентированная магнитная стрелка указывает своим северным полюсом направление магнитного поля. Для наглядного изображения магнитных полей используют силовые линии. Силовой линией магнитного поля называют такую линию, в каждой точке которой магнитное поле направлено по касательной к этой линии. Картину магнитных силовых линий можно сделать «видимой». Для этого используют мелкие железные опилки, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль силовых линий. В отличие от потенциального электростатического поля, где силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных, магнитное поле является соленоидальным или вихревым: его силовые линии всегда замкнуты. Другими словами, магнитное поле не имеет магнитных зарядов.
Силовой характеристикой магнитного поля служит вектор магнитной индукции  . Вектор
. Вектор  можно ввести одним из трех эквивалентных способов:
можно ввести одним из трех эквивалентных способов:
а) исходя из силового действия магнитного поля на движущегося в нем точечного электрического заряда — силы Лоренца;
б) основываясь на силовом действии магнитного поля на малый элемент проводника с током — силы Ампера;
в) исходя из силового действия магнитного поля на небольшую рамку с током.
Сила Лоренца
На частицу с электрическим зарядом q, движущуюся в магнитном поле со скоростью 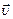 действует сила Лоренца равная
действует сила Лоренца равная 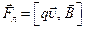 . Направление силы Лоренца определится по правилу векторного произведения — правилу левой руки. Четыре вытянутых пальца левой руки располагают по направлению вектора
. Направление силы Лоренца определится по правилу векторного произведения — правилу левой руки. Четыре вытянутых пальца левой руки располагают по направлению вектора 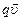 (по направлению движения положительного заряда и против движения отрицательного заряда), в ладонь входят силовые линии магнитного поля, тогда большой вытянутый палец покажет направление действия силы Лоренца.
(по направлению движения положительного заряда и против движения отрицательного заряда), в ладонь входят силовые линии магнитного поля, тогда большой вытянутый палец покажет направление действия силы Лоренца.
По модулю сила Лоренца будет равна 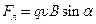 , где
, где 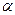 — угол между вектором
— угол между вектором 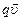 и направлением поля,
и направлением поля, 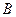 — индукция магнитного поля, определяемая как отношение максимальной силы, действующей на заряженную частицу со стороны магнитного поля, к произведению абсолютной величины заряда и скорости частицы
— индукция магнитного поля, определяемая как отношение максимальной силы, действующей на заряженную частицу со стороны магнитного поля, к произведению абсолютной величины заряда и скорости частицы 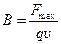 . Сила максимальна при движении частицы перпендикулярно магнитному полю,
. Сила максимальна при движении частицы перпендикулярно магнитному полю, 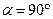 .
.
Это отношение не зависит, как показывает опыт, ни от q, ни от 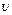 и характеризует магнитное поле в точке нахождения заряда.
и характеризует магнитное поле в точке нахождения заряда.
Если на движущийся электрический заряд действует не только магнитное поле с индукцией  , но также еще и электрическое поле с напряженностью
, но также еще и электрическое поле с напряженностью 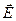 , то результирующая сила
, то результирующая сила 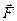 будет равна
будет равна
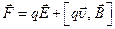 .
.
Эту силу 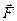 часто также называют силой Лоренца, а иногда обобщенной силой Лоренца.
часто также называют силой Лоренца, а иногда обобщенной силой Лоренца.
Если заряженная частица движется вдоль силовой линии магнитного поля, 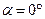 , то в этом случае сила Лоренца равна нулю, и частица будет двигаться, не изменяя направления своего движения по прямой линии.
, то в этом случае сила Лоренца равна нулю, и частица будет двигаться, не изменяя направления своего движения по прямой линии.
Если заряженная частица движется перпендикулярно магнитному полю, 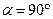 , то в этом случае она будет двигаться по окружности, радиус которой определится из второго закона Ньютона:
, то в этом случае она будет двигаться по окружности, радиус которой определится из второго закона Ньютона: 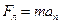 ,
, 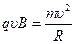 . Откуда
. Откуда 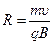 , а период обращения будет равен
, а период обращения будет равен 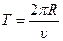 ,
, 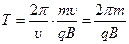 .
.
Если заряженная частица движется под острым углом 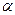 к магнитному полю, то в этом случае она будет двигаться по спирали. Действительно, вектор скорости
к магнитному полю, то в этом случае она будет двигаться по спирали. Действительно, вектор скорости 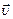 можно разложить на две составляющие
можно разложить на две составляющие 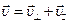 , где
, где 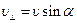 ,
, 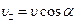 . Вектор
. Вектор 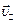 не изменяется ни по направлению, ни по величине, вектор
не изменяется ни по направлению, ни по величине, вектор 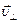 все время изменяется по направлению — в итоге частица будет двигаться по спирали, радиус которой будет равен
все время изменяется по направлению — в итоге частица будет двигаться по спирали, радиус которой будет равен 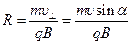 , а шаг спирали
, а шаг спирали 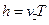 ,
, 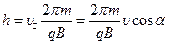 .
.
Принцип действия циклических ускорителей заряженных частиц.
Независимость периода вращения 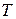 заряженной частицы в магнитном поле была использована американским ученым Лоуренсом в идеи циклотрона — ускорителе заряженных частиц.
заряженной частицы в магнитном поле была использована американским ученым Лоуренсом в идеи циклотрона — ускорителе заряженных частиц.
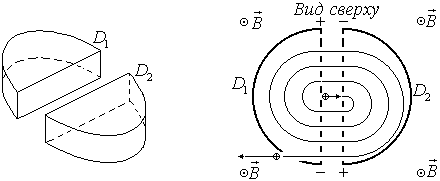 |
Циклотрон состоит из двух дуантов 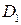 и
и 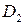 — полых металлических полуцилиндров, помещенных в высокий вакуум. Ускоряющее электрическое поле создается в зазоре между дуантами. Заряженная частица попадая в этот зазор увеличивает скорость движения и влетает в пространство полуцилиндра (дуанта). Дуанты помещаются в постоянное магнитное поле, и траектория частицы внутри дуанта будет искривляться по окружности. Когда частица во второй раз войдет в зазор между дуантами, полярность электрического поля изменяется и оно снова становится ускоряющим. Увеличение скорости сопровождается увеличением радиуса траектории. Практически к дуантам прикладывается переменное поле с частотой
— полых металлических полуцилиндров, помещенных в высокий вакуум. Ускоряющее электрическое поле создается в зазоре между дуантами. Заряженная частица попадая в этот зазор увеличивает скорость движения и влетает в пространство полуцилиндра (дуанта). Дуанты помещаются в постоянное магнитное поле, и траектория частицы внутри дуанта будет искривляться по окружности. Когда частица во второй раз войдет в зазор между дуантами, полярность электрического поля изменяется и оно снова становится ускоряющим. Увеличение скорости сопровождается увеличением радиуса траектории. Практически к дуантам прикладывается переменное поле с частотой 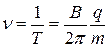 . Скорость частицы каждый раз увеличивается в промежутке между дуантами под действием электрического поля.
. Скорость частицы каждый раз увеличивается в промежутке между дуантами под действием электрического поля.
Эффект Холла.
В 1879 г. американским физиком Е. Х. Холлом был открыт эффект названный его именем.
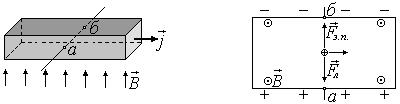 Вид сверху Вид сверху |
Если взять пластинку из металла или полупроводника и пропустить через неё ток, то при помещении пластинки в магнитное поле 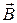 между точками «а» и «б» возникает разность потенциалов
между точками «а» и «б» возникает разность потенциалов 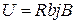 ,где
,где  — постоянная Холла,
— постоянная Холла, 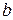 — ширина пластинки,
— ширина пластинки, 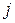 — плотность тока,
— плотность тока, 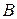 —индукция магнитного поля. Рассмотрим эффект Холла с теоретической точки зрения.
—индукция магнитного поля. Рассмотрим эффект Холла с теоретической точки зрения.
На каждый движущийся заряд действует сила Лоренца, в результате чего происходит перераспределение заряда и возникновение поперечного электрического поля. Распределение зарядов будет происходить до тех пор, пока сила Лоренца не скомпенсируется силой со стороны возникшего поперечного электрического поля 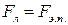 . То есть
. То есть 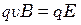 , отсюда
, отсюда 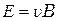 . Из формулы плотности тока
. Из формулы плотности тока 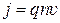 выразим скорость направленного движения заряженных частиц
выразим скорость направленного движения заряженных частиц 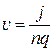 . Тогда
. Тогда 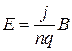 , а холовская разность потенциалов
, а холовская разность потенциалов 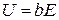 будет вычисляться по формуле
будет вычисляться по формуле 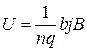 . В металлах в создании тока участвуют электроны. Заряд электрона равен элементарному заряду, и формула эффекта Холла для металлов принимает вид
. В металлах в создании тока участвуют электроны. Заряд электрона равен элементарному заряду, и формула эффекта Холла для металлов принимает вид
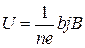 .
.
Сравнивая эту формулу с экспериментальной получим, что постоянная Хола для металлов будет равна 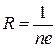 .
.
По знаку холовской разности потенциалов можно определить знак носителей тока, т. е., какие частицы, положительные или отрицательные участвуют в создании тока.
Измерив постоянную Холла 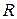 и зная заряд носителя тока
и зная заряд носителя тока 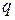 , можно определить их концентрацию
, можно определить их концентрацию 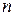 .
.
Существуют датчики Холла, позволяющие измерять индукцию магнитного поля 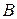 .
.
