Кинематика поступательного и вращательного движения

Кафедра физики

ОБЩАЯ ФИЗИКА (ОСНОВЫ ФИЗИКИ)

Учебное пособие для самостоятельной работы

И индивидуальные домашние задания

Для студентов технических специальностей и направлений подготовки

Вологда

УДК 53(07.072)

Общая физика (основы физики): учебное пособие для самостоятельной работы и индивидуальные домашние задания для студентов технических специальностей и направлений подготовки. - Вологда: ВоГУ, 2014. - 130 с.

Учебное пособие подготовлено в соответствии с программой курса общей физики (основы физики) для студентов инженерно-технических специальностей и направлений подготовки. Наряду с курсом лекций по общей физике, оно продолжает линейку учебно-методических материалов для студентов первого курса технических специальностей и направлений, рабочие программы которых содержат пропедевтические курсы «Общая физика» или «Основы физики».

В пособии содержится 90 вариантов задач по базовым темам курса общей физики (механика, термодинамика, электростатика, постоянный ток, магнетизм), которые рекомендуется использовать в качестве индивидуальных домашних заданий (ИДЗ) при изучении курса общей физики.

Значительную часть пособия занимают краткое изложение теоретического материала и примеры решения задач по каждой теме. Пособие может быть использовано для самостоятельной работы как при решении задач, так и для повторения теоретического материала, а также как краткий справочник при подготовке к экзаменам и зачётам. Пособие может быть рекомендовано также всем студентам, недостаточно подготовленным к изучению физики в вузе, для укрепления базовых знаний по основам физики и подготовки к восприятию материала вузовской программы.

Утверждено редакционно-издательским советом ВоГУ

Составители: А.В.Андреева, ст. преподаватель

Л.А.Кузина, канд.физ.-мат.наук, доцент

О.Ю.Штрекерт, канд.физ.-мат.наук, доцент

Рецензенты: В.А.Горбунов, д-р физ.-мат. наук, профессор, зав. кафедрой ИТ

А.И.Домаков, канд.техн. наук, профессор ВоГПУ

Требования к оформлению и общие методические указания

1. Задачи оформляются в письменном виде в тетради или на отдельных листах. Решение каждой задачи необходимо начинать с новой страницы.

2. Требуется указать номер варианта и номер задачи.

3. Условие задачи переписывается полностью, без сокращений.

4. Решение записывается в стандартном виде:

Дано:	Решение:
Найти:
Ответ:

5. Все физические величины необходимо выразить в системе единиц СИ.

6. Сделать рисунок, схему, если это необходимо.

7. Сформулировать основные законы, записать формулы, на которых базируется решение. Обосновать возможность их применения в условиях данной задачи. Составить полную систему уравнений для решения задачи.

8. Получить окончательное выражение искомой величины в общем виде. Проверить размерность.

9. Подставить числовые данные и рассчитать искомую величину.

10.Проанализировать полученный результат.

11.Записать ответ.

12.Каждую задачу требуется защитить устно на собеседовании, продемонстрировав владение материалом; то есть полностью объяснить решение задачи (обосновать решение, сформулировав использованные физические законы и определения).

Кинематика поступательного и вращательного движения

Краткая теория

· Радиус-вектор материальной точки задаёт положение её в пространстве (рис.1.1):

,

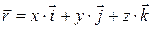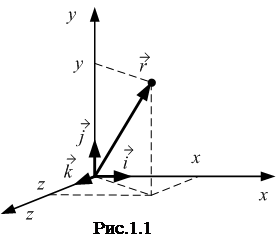где x, y и z – координаты точки; 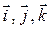– единичные векторы (орты), направленные вдоль осей OX, OY и OZ соответственно. Модуль вектора :

.

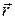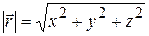· Кинематическое уравнение движения:

;

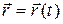или в координатной форме:

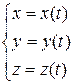
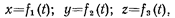где t – время.

· Средняя скорость:

,

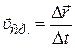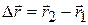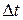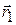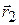где – перемещение материальной точки за интервал времени , и – радиус-векторы начального и конечного положения точки соответственно.

· Средняя путевая скорость (средняя скорость вдоль траектории):

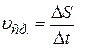
где 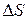– путь (длина траектории), пройденный точкой за интервал времени .

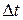· Мгновенная скорость:

; ,

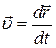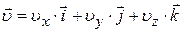где 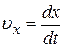, , 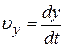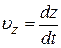– проекции скорости 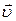на оси координат.

· Модуль скорости:

.

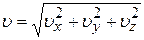· Закон сложения скоростей:

,

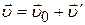где 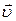– абсолютная, 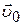– переносная, 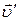– относительная скорости.

· Ускорение:

; ,

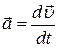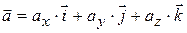где 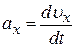, , 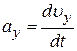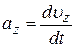– проекции ускорения 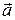на оси координат.

· Модуль ускорения: .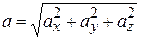

· При равномерном движени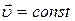и и .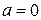

· Кинематическое уравнение равномерного движения материальной точки:

,

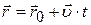или вдоль оси х:

,

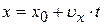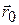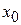где и – радиус-вектор и координата начального положения точк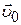и; и 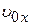– начальная скорость и её проекция на ось OX; t – время.

· При равнопеременном движении .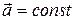

· Скорость точки при равнопеременном движении:

,

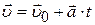или в проекции на ось OX:

.

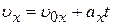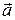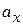где и – ускорение и его проекция на ось OX.

· Кинематическое уравнение равнопеременного движения:

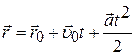
или вдоль оси x:

.

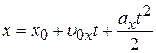Криволинейное движение

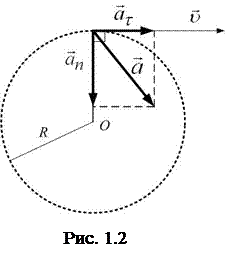
· Ускорение при криволинейном движенииможно представить как сумму нормальной 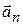и тангенциальной 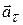составляющих (рис.1.2):

;

.

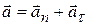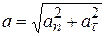· Нормальное ускорение равно

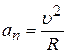
и направлено к центру кривизны траектории перпендикулярно ей. Здесь R – радиус кривизны траектории в данной точке.

· Тангенциальное (касательное) ускорение равно

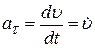
и направлено по касательной к траектории.

· Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением) φ.

· Кинематическое уравнение вращательного движения:

.

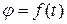· Средняя угловая скорость:

,

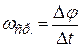где 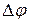–угол поворота за интервал времени .

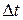· Мгновенная угловая скорость:

.

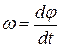· Угловое ускорение:

.

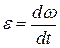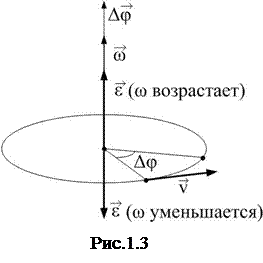
Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с осью вращения (рис.1.3).

· Связь между угловыми величинами и линейными:

;

;

,

,

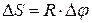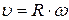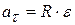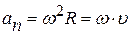где 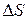– путь, пройденный точкой по дуге окружности радиусом R, 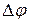– соответствующий угол поворота,

· При равномерном вращении , .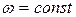

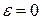· Кинематическое уравнение равномерного вращения:

,

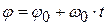где 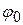– начальная угловая координата; t – время.

· Частота вращения:

,

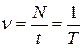где N – число оборотов, совершаемых телом за время t; Т – период вращения (время одного полного оборота).

· Связь угловой скорости с периодом и частотой:

.

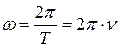· При равнопеременном вращательном движении .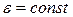

· Угловая скорость при равнопеременном вращении:

,

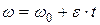где 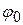– начальная угловая координата; 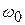– начальная угловая скорость, t – время, ε – угловое ускорение.

· Кинематическое уравнение равнопеременного вращения ( .)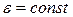

.

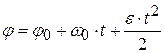Примеры решения задач

Пример 1.1.Уравнение движения точки по плоскости имеет вид: 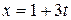, 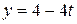(x и y измеряются в метрах, t – в секундах). Какова скорость точки? Получить уравнение траектории и построить её.

Дано: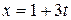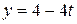

Найти: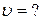

Решение

Найдём проекции скорости точки на координатные оси, продифференцировав уравнение движения:

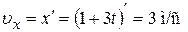
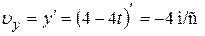
Модуль скорости по теореме Пифагора:

.

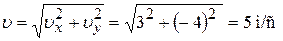Уравнение траектории получим, исключив время t:

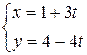
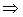
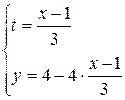
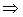
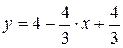; или

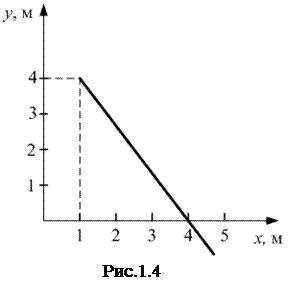
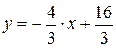– это уравнение траектории. Траекторией будет прямая линия (рис.1.4). Движение начинается в точке с координатами 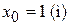, 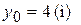. Если 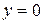, то 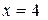. По двум точкам можно построить прямую линию.

Ответ: ; .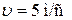

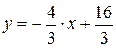Пример 1.2.Тело свободно (без начальной скорости) падает с некоторой высоты H. Путь, пройденный им за последнюю секунду, в 7 раз больше пути, пройденного за первую секунду. Определить время падения t и высоту H.

Дано: t1=1 c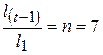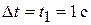

Найти: t=? H=?

Решение

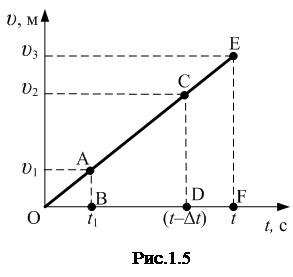Используется графический способ решения задачи. На рис.1.5 дан график зависимости скорости от времени при свободном падении без начальной скорости. Площадь под графиком равна пройденному пути. По условию, путь, пройденный за последнюю секунду, в 7 раз больше пути, пройденного за первую секунду: 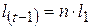, следовательно, площадь трапеции CDFE в n=7 раз больше площади треугольника OAB:

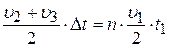(1)

Скорости при равнопеременном движении для каждого момента времени можно найти по общей формуле: 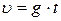(так как ):

; ; .

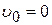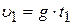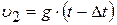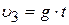Здесь t – полное время падения. Тогда из (1):

.

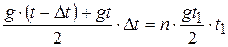После сокращения на 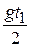с учётом :

;

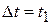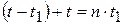
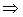
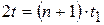
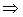
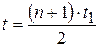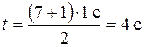
Высота – путь за время t – это площадь треугольника OFE:

;

.

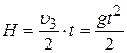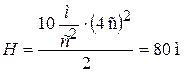Ответ: t=4 c; H=80 м.