Законы постоянного тока

Краткая теория

· Сила постоянного тока

,

где – заряд, прошедший через сечение проводника за время .

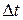· Плотность тока – это отношение силы тока к площади сечения проводника :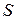

.

· Плотность тока равна

,

где – концентрация свободных носителей заряда в проводнике, – заряд каждой частицы, 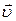– средняя скорость их направленного движения.

· Сопротивление однородного проводника

,

где ρ – удельное сопротивление вещества проводника; l – его длина S – его сечение.

· Проводимость G проводника и удельная проводимость γ вещества

; .

· Зависимость сопротивления R и удельного сопротивления ρот температуры:

; ,

где ρ₀ (R₀) – удельное сопротивление (сопротивление) при температуре 0 С; t –температура (по шкале Цельсия); α – температурный коэффициент сопротивления.

· Сопротивление при последовательном соединении проводников:

· Сопротивление при параллельном соединении проводников:

.

Здесь R_k – сопротивление k-го проводника; N – число проводников.

· Электродвижущая сила (ЭДС) численно равна работе сторонних сил по перемещению единичного заряда по замкнутой цепи. Или: ЭДС равна работе сторонних сил по перемещению точечного заряда по замкнутой цепи, отнесённой к величине этого заряда:

.

· Закон Ома:

для неоднородного участка цепи (участка, содержащего ЭДС):

;

для однородного (не содержащего ЭДС) участка цепи: ;

для замкнутой цепи: .

Здесь (φ₁ – φ₂) – разность потенциалов на концах участка цепи; ε – ЭДС источника тока, U – напряжение на участке цепи; R – сопротивление цепи (участка цепи); r – внутреннее сопротивление источника тока.

· Мощность тока

P=I∙U.

· Закон Джоуля-Ленца

Q=I²∙R∙t,

где Q – количество теплоты, выделяющееся в участке цепи при протекании постоянного тока за время t.

· Коэффициент полезного действия источника тока:

Примеры решения задач

Пример 7.1.Потенциометр с сопротивлением R=100 Ом подключен к источнику тока, ЭДС ε которого равна 150 В и внутреннее сопротивление r=50 Ом (рис. 7.1). Определить показание вольтметра с сопротивлением R_B=500 Ом, соединенного проводником с одной из клемм потенциометра и подвижным контактом с серединой обмотки потенциометра. Какова разность потенциалов между теми же точками потенциометра при отключенном вольтметре?

Дано: R=100 Ом ε=150 В r=50 Ом RB=500 Ом

Найти: U2=?

Решение

Показание U₁ вольтметра, подключенного к точкам А и В (рис. 7.1), определяется по закону Ома:

U₁=I₁R₁, (1)

где I₁ – сила тока в неразветвлённой части цепи; R₁ – сопротивление параллельно соединенных вольтметра и половины потенциометра.

Силу тока I₁ найдем по закону Ома для всей цепи:

, (2)

где – сопротивление внешней цепи.

Внешнее сопротивление есть сумма двух сопротивлений:

. (3)

Сопротивление R₁ параллельного соединения может быть найдено по формуле откуда

R_l=R∙R_B/(R + 2R_B).

Вычисления: R_l=100∙500/(100+ 2^.500)=45.5 Ом.

Подставив в выражение (2) выражение для из (3), определим силу тока:

.

Если подставить значения I₁ и R₁ в формулу (1), то найдем показание вольтметра: U₁=46,9 В.

Разность потенциалов между точками А и В при отключенном вольтметре равна произведению силы тока I₂ на половину сопротивления потенциометра:

,

причём . Тогда . Вычисления: .

Ответ: U₂=50 В.

8. Электромагнетизм

Краткая теория

· Магнитный момент контура с током:

,

где I – сила тока в контуре, S – его площадь, – единичный вектор нормали к контуру (рис.8.1). Если контур имеет N витков, то .

· Индукция магнитного поля В – отношение максимального вращающего момента М_max к магнитному моменту контура:

· Принцип суперпозиции: если в данной точке пространства различные источники создают магнитные поля, магнитные индукции которых равны , …, , то результирующая индукция поля в этой точке равна:

.

· Закон Ампера. Сила, действующая на проводник с током в магнитном поле (сила Ампера), направлена по правилу левой руки (рис.8.2) и равна

F=B∙I∙l∙sinα,

где I – сила тока; l – длина проводника; – магнитная индукция поля, α – угол между проводником и вектором .

· Индукция магнитного поля прямолинейного проводника с током I бесконечной длины на расстоянии r от проводника:

,

где – магнитная постоянная, μ – магнитная проницаемость среды (для вакуума μ=1). Направление тока и магнитной индукции связаны правилом буравчика (рис.8.3).

· Магнитная проницаемость среды μпоказывает, во сколько раз индукция магнитного поля в среде возрастает по сравнению с вакуумом:

,

где B – индукция магнитного поля в среде, B₀ – в вакууме.

· Индукция магнитного поля в центре кругового витка с током I равна

и направлена по правилу правого винта (рис.8.4). Здесь R – радиус витка.

· Сила взаимодействия двух параллельных бесконечных проводников с токами I₁ и I₂, находящимися на расстоянии r, в расчёте на единицу длины проводника:

.

· Момент сил, действующий на контур с током в магнитном поле:

,

где В – индукция поля, p_m – магнитный момент контура, α – угол между вектором магнитной индукции и магнитным моментом .

· Сила Лоренца (сила, действующая на заряд q, движущийся со скоростью в магнитном поле с индукцией ):

,

где a – угол, образованный вектором скорости движущейся частицы и вектором индукции магнитного поля.

· Магнитный поток (поток вектора магнитной индукции В) через поверхность площадью S:

,

где 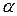– угол между вектором 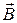и нормалью к поверхности (рис.8.5).

· Работа по перемещению контура с током в магнитном поле

A=I∙DФ,

где DФ – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром; I – сила тока в контуре.

· Закон Фарадея (закон электромагнитной индукции): ЭДС индукции в замкнутом контуре равна по величине и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром

, точнее .

Если контур содержит N витков, то , или , где – полное потокосцепление.

Частные случаи применения закона Фарадея:

а) разность потенциалов U на концах проводника длиной l, движущегося со скоростью u в однородном магнитном поле индукцией B:

U=B∙l∙u∙sina,

где a – угол между направлениями векторов скорости u и магнитной индукции В;

б) электродвижущая сила индукции , возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью ω в однородном магнитном поле с индукцией В:

,

где wt — мгновенное значение угла между вектором и вектором нормали к плоскости рамки.

· Индуктивность контураLчисленно равна магнитному потоку Ф, пронизывающему контур, при единичной силе тока в контуре:

.

Для катушки с N витками , где Ψ=NФ – полное потокосцепление.

· Индуктивность соленоида (рис.8.6):

,

где N – число витков, l – длина соленоида, S – площадь сечения соленоида.

· ЭДС самоиндукции , возникающая в катушке с индуктивностью L, при изменении силы тока в ней:

, или .

· Энергия магнитного поля контура с током:

.

Для катушки с N витками .

· Закон сохранения энергии для идеального колебательного контура:

.

Примеры решения задач

Пример 8.1.Электрон, пройдя ускоряющую разность потенциалов U=400 В, попал в однородное магнитное поле с индукцией B=1,5 мТл. Определить радиус кривизны траектории и частоту вращения электрона в магнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.

Решение

На движущийся в магнитном поле электрон действует сила Лоренца (действием силы тяжести можно пренебречь):

.

Дано: U=400 В B=1,5 мТл α=900 m=9.1.10-31 кг е=1.6.10-19

Найти: R=? ν=?

Вектор силы Лоренца перпендикулярен вектору скорости и, следовательно, по второму закону Ньютона , сообщает электрону нормальное (центростремительное) ускорение :

.(1)

Кинетическая энергия, приобретённая электроном в ускоряющем поле, есть работа сил поля ; , откуда скорость , или с учётом (1):

. (2)

Частота – обратная периоду вращения величина: . Период – время одного оборота, то есть время прохождения пути, равного длине окружности :

С учётом (1): .

Вычисления: ;

Ответ: ; .

Пример 8.2.Электрон движется в однородном магнитном поле с индукцией В=0,03 Тл по окружности радиусом R=10 см. Определить скорость u электрона.

Дано: В=0,03 Тл R=10 см

Найти: u=?

Решение

Попробуем решить эту задачу аналогично предыдущей:

.

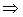
Полученное значение скорости больше скорости света: . Следовательно, приведённое решение неверное. Правильное решение должно учитывать формулы теории относительности: классическая механика при скоростях, сравнимых со скоростью света, не работает. Необходимо:

1) Вместо второго закона Ньютона в классической формулировке использовать второй закон Ньютона в импульсной форме:

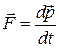. (1)

2) Вместо определения классического импульса использовать релятивистский импульс:

(2)

Вычислим производную импульса, помня, что при равномерном вращении по окружности скорость изменяется только по направлению, но не по величине (υ=const):

. (3)

Здесь – полное ускорение по определению. Поскольку касательное (тангенциальное) ускорение отсутствует ( ), то полное равно нормальному: ; тогда . Из (1) и (3) получим выражение для силы:

.

Подставим выражение для силы Лоренца ( ) и преобразуем:

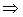
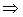
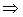
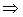
. Вычисления: ; .

Ответ: .

Пример 8.3.Виток, по которому течет ток I=20 А, свободно установился в однородном магнитном поле В=16 мТл. Диаметр d витка равен 10 см. Какую работу нужно совершать, чтобы медленно повернуть виток на угол Δa=p/2 относительно оси, совпадающей с диаметром?

Дано: I=20 А В=16 мТл d=10 см Δa=p/2

Найти: Aвнеш.=?

Решение

При неизменной силе тока в контуре работа при повороте контура равна

A=I∙DФ=I∙(Ф₂–Ф₁),

где Ф₁ и Ф₂ – магнитные потоки, пронизывающие контур в начальном и конечном положениях.

Так как в начальном положении контур установился свободно (положение устойчивого равновесия), то момент внешних сил, действующий на контур ( ), равен нулю. В этом положении угол a₁ между вектором магнитного момента и магнитной индукцией 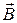равен нулю: a₁=0. По определению магнитного потока Ф₁=В∙S∙cosa₁=В∙S, где – площадь контура. После поворота контура угол a₂=a₁+Δa=p/2, и магнитный поток Ф₂=В∙S∙cosa₂=0.

Работа внешних сил равна по величине и противоположна по знаку работе сил поля, тогда

A_внеш.= –A=I∙Ф₁=I∙В∙S∙, или .

Вычисления: .

Ответ: .

Пример 8.4. В однородном магнитном поле с индукцией B=0,1 Тл равномерно вращается рамка, содержащая N=1000 витков, с частотой ν=10 Гц. Площадь S рамки равна 150 см². Определить мгновенное значение ЭДС, соответствующее углу поворота рамки 30°.

Дано: B=0,1 Тл N=1000 ν=10 Гц S=150 см2 α=30°

Найти:

Решение

При вращении рамки с угловой скоростью в постоянном магнитном поле угол между нормалью к рамке и индукцией поля изменяется по закону:

, (1)

где циклическая частота связана с линейной частотой:

. (2)

Полное потокосцепление (суммарный магнитный поток через все N витков), также изменяется:

.

По закону Фарадея ЭДС индукции, возникающая в рамке, равна

;

;

С учётом (1) и (2):

.

Вычисления:

Ответ: .

Пример. 8.5. По соленоиду течет ток I=2 А. Магнитный поток Ф, пронизывающий поперечное сечение соленоида, равен 4 мкВб. Определить индуктивность L соленоида, если он имеет N=800 витков.

Решение

Дано: I=2 А Ф=4 мкВб N=800

Найти: L=?

По определению, индуктивность соленоида – это коэффициент пропорциональности между потокосцеплением Y и силой тока I:

.

Полное потокосцепление Y – суммарный магнитный поток через все витки: Ψ=NФ,

где Ф – поток через один виток соленоида. Тогда

.

Вычисления: .

Ответ: .

Пример 8.6. При скорости изменения силы тока в соленоиде, равной 50 А/с, на его концах возникает ЭДС самоиндукции 0.08 В. Определить индуктивность L соленоида.

Решение

По определению, индуктивность соленоида – это коэффициент пропорциональности между потокосцеплением Y и силой тока I: . По закону Фарадея ЭДС самоиндукции, возникающая в контуре, равна быстроте изменения полного магнитного потока: . Или: .

Дано:

Найти: L=?

Знак «минус» можно опустить, поскольку направление ЭДС в данном случае несущественно. Далее:

,

где и – начальное и конечное потокосцепление.

Тогда . Вычисления: .

Ответ: .

Варианты задач

Вариант 1

1. К покоящемуся на шероховатой горизонтальной поверхности телу приложена нарастающая с течением времени горизонтальная сила тяги F=b^.t, где b – постоянная величина. На рисунке 1 представлен график зависимости ускорения тела от времени действия силы. Определите коэффициент трения скольжения.

2. Воду массой 500 г при температуре 95⁰С налили в теплоизолированный сосуд, где находился твердый нафталин при температуре 80⁰С. После установления теплового равновесия температура воды оказалась равна 80⁰С, при этом весь нафталин перешел в жидкое состояние. Пренебрегая потерями тепла, оцените, чему равна масса нафталина в сосуде.

3. Заряженная пылинка движется между двумя одинаковыми заряженными вертикальными пластинами, расположенными напротив друг друга. Разность потенциалов между пластинами 500 В, масса пылинки столь мала, что силой тяжести можно пренебречь. Какую кинетическую энергию приобретает пылинка при перемещении от одной пластины, если ее заряд 4 нКл? Ответ выразить в мкДж и округлить до целых.

4. Батарея дает максимальную силу тока I_mах=5 А. Максимальное количество теплоты Q, которое может выделить эта батарея во внешней цепи за время t=10 с, равно 100 Дж. Найдите ЭДС батареи.

5. Какое количество теплоты подведено к двум молям одноатомного идеального газа при осуществлении процесса 1–2–3 (рис.2), если начальный объем его равен V₁=1 л, а давление равно p₁=100 кПа?

6. В магнитном поле с большой высоты падает с постоянной скоростью υ металлическое кольцо, имеющее диаметр d и сопротивление R. Плоскость кольца все время горизонтальна. Найдите массу кольца, если модуль индукции В магнитного поля изменяется с высотой Н по закону |В|=В₀(1+αН). Сопротивлением воздуха пренебречь.

Вариант 2

1. Два поезда прошли одинаковый путь за одно и то же время. Однако один поезд, трогаясь с места, прошел весь путь равноускоренно с ускорением а=3 см/с², а другой поезд половину пути шел со скоростью υ₁=18 км/ч, а другую половину – со скоростью υ₂=54 км/ч. Найдите пройденный путь.

2. Два шарика, массы которых m₁=200 г и m₂=300 г, подвешены на одинаковых нитях длиной L=50 см. Шарики соприкасаются. Первый шарик отклонили от положения равновесия на угол α=90° и отпустили. После абсолютно неупругого соударения шарики поднимутся на высоту, равную ... см.

3. Удельная теплоемкость меди равна 380 Дж/(кг^.К), а удельная теплоемкость воды 4200 Дж/(кг^.К). Нагретый до температуры 70°С кусок меди массой 2 кг опускают в сосуд с водой, масса которой 4 кг. Начальная температура воды равна 20⁰С. Определите температуру, которая установится в сосуде (в ⁰С), если известно, что потери тепла малы.

4. Один моль идеального одноатомного газа сначала охладили, а затем нагрели до первоначальной температуры 300 К, увеличив объем газа в 3 раза (см. рис.1). Какое количество теплоты отдал газ на участке 1–2?

5. На схеме, изображенной на рисунке 2, ЭДС источника ε=95 В, внутреннее сопротивление r=0,5 Ом. Сопротивления внешней цепи R₁=R₃=6 Ом, R₂=R₄=12 Ом. Показание амперметра равно … А.

6. Электрон влетает в область однородного магнитного поля с индукцией В=0,01 Тл со скоростью υ=1000 км/с перпендикулярно линиям магнитной индукции. Какой путь он пройдет к тому моменту, когда вектор скорости повернется на 1 градус?

Вариант 3

1. Автомобиль едет по горизонтальному участку дороги, затем въезжает на вогнутый мостик, имеющий форму дуги окружности. В нижней точке мостика автомобиль оказывает на него давление, в 3 раза большее, чем на горизонтальном участке дороги. Скорость автомобиля равна υ=72 км/ч. Радиус кривизны мостика равен …. м. Ответ округлить до целого.

2. Некоторое количество гелия расширяется: сначала – изобарно, затем – изотермически, совершая при этом работу А=3 Дж. Начальная и конечная абсолютные температуры отличаются в 2 раза. Начальные давление и объём: p₁=1 кПа, V₁=2л. Найти количество теплоты Q, полученное газом в этом процессе.

3. Ученик с помощью нагревательного элемента (спирали) нагревает парафин (рис.1) массой т=50 г, находящийся в сосуде при температуре плавления. Весь парафин расплавился за t=8 мин. Спираль и амперметр последовательно подсоединены к источнику постоянного тока с напряжением U=14 В. Показание амперметра равно I=2,5 А. Сопротивлением амперметра пренебречь. Удельная теплота плавления парафина r=147 кДж/кг. На нагревание парафина пошло …. % теплоты, выделившейся в спирали. Ответ округлите до целого.

4. Плоская горизонтальная фигура площадью 0,1 м², ограниченная проводящим контуром с сопротивлением 5 Ом, находится в однородном магнитном поле. Пока проекция магнитной индукции на вертикаль ОZ медленно и равномерно убывает от некоторого начального значения B_1z до конечного значения B_2z= –0,1Тл, по контуру протекает заряд 0,008 Кл. Найдите B_1z, если ось ОZ перпендикулярна плоскости фигуры.

5. В электрической цепи, показанной на рисунке 2, внутреннее сопротивление источника постоянного тока равно r=6 Ом, сопротивления резисторов R₁=40 Ом, R₂= 60 Ом. Через источник ЭДС течёт ток, сила которого равна I = 5 А. Величина ЭДС источника постоянного тока равна ε= ...В.

6. Шар массой т=200 г, заряженный зарядом q=20 мкКл, висит на пружинке в однородном электрическом поле (рис.3). Жесткость пружины k=20 Н/м. Напряженность электрического поля Е=2^.10⁴ Н/Кл. Пружина находится в растянутом состоянии, при этом её деформация равна Δl=...см.

Вариант 4

1. Через какое время после выстрела стрела, пущенная вертикально вверх со скоростью 12 м/с, первый раз оказывается на высоте 4 м? Ответ округлить до десятых.

2. Воду массой 100 г при температуре 12⁰С поместили в калориметр, где находился лед при температуре –5⁰С. После установления теплового равновесия температура льда повысилась до 0⁰С, но масса льда не изменилась. Пренебрегая потерями тепла, оцените, какова была начальная масса льда в калориметре.

3. Пылинка массой 10^–9 г несет на себе заряд 10^–8 Кл и движется вертикально между двумя одинаковыми горизонтальными пластинами, расположенными напротив друг друга, разность потенциалов между которыми 200 В. На сколько изменится кинетическая энергия пылинки при перемещении от одной пластины до другой на расстояние 1 см? Ответ выразить в мкДж и округлить до целых.

4. Стальной шарик массой m=780 г удерживается силой F=28 Н с помощью стержня, один конец которого на шарнире прикреплен к стене (см. рис.1). Длина стержня L=80 см, масса М=400 г. Затем шарик опускают в сосуд с водой. Как следует изменить точку приложения силы F, чтобы стержень при этом остался в горизонтальном положении?

5. Две параллельные шины, подключенные к аккумулятору с ЭДС ε₀ и внутренним сопротивлением r, находятся в однородном магнитном поле с индукцией В. Шины замкнуты проводником длиной l и сопротивлением R, который перемещается по шинам без нарушения контакта перпендикулярно полю со скоростью υ. Пренебрегая сопротивлением шин, определите напряжение на зажимах источника, мощность тепловых потерь в проводнике, а также механическую мощность, подводимую к проводнику.

6. Над идеальным одноатомным газом в количестве вещества 1,4 моль совершили процесс 1–2–3–1 (рис.2). Какое количество теплоты подведено к системе на участке 1–2, если температура газа в точке 3 равна 580 К?

Вариант 5

1. Брусок массой М=1,8 кг и шарик массой т связаны между собой невесомой и нерастяжимой нитью, как показано на рисунке 1. Брусок находится на плоскости, составляющей угол α=45° с горизонталью. Коэффициент трения между поверхностью и телом равен μ=0,2. Чему равно максимальное значение массы т, при котором брусок с нулевой начальной скоростью начинает движение вниз?

2. По гладкой горизонтальной поверхности со скоростью υ₁=1 м/с скользит шайба массой т₁=90 г и налетает на неподвижную шайбу с массой m₂=100 г. Рассчитайте энергию, которая перешла во внутреннюю при этом ударе, если после него первая шайба остановилась.

3. Аргон расширяется сначала адиабатно, потом изотермически, при этом конечная абсолютная температура в два раза ниже начальной. Совершенная газом за весь процесс работа А=5 Дж. Какое количество тепла было получено газом в процессе, если начальное давление и объем p₁=1 кПа, V₁= 4 л?

4. Полый пластмассовый шарик радиусом R=2 см имеет отверстие А диаметром d=1 мм (см. рис.2). Шарик постоянно равномерно заряжен отрицательным зарядом Q=–10^–12 Кл. К шарику из точки, удаленной от него на расстояние r>>R, по прямой АО движется электрон с начальной скоростью υ₀=10⁶ м/с. Попав в отверстие, он ударяется о стенку шарика. Найдите кинетическую энергию электрона перед ударом.

5. Из проволоки, единица длины которой имеет сопротивление ρ, сделан плоский замкнутый контур, состоящий из двух квадратов площадью S₁ и S₂ (рис.3). Контур находится в однородном магнитном: поле с индукцией В₀, направленной перпендикулярно плоскости контура. Какой заряд протечет через поперечное сечение провода при равномерном уменьшении индукции поля? Между пересекающимися на рисунке проводами контакта нет.

6. Два источника тока с одинаковой ЭДС и внутренними сопротивлениями r₁=1 Ом, r₂=2 Ом как при параллельном, так и при последовательном присоединении к одному и тому же внешнему сопротивлению показывают одну и ту же силу тока. Определите внешнее сопротивление.

Вариант 6

1. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены противоположно и равны υ_пл=15 м/с и υ_бр=5 м/с. Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом μ=0,17. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится на 30%?

2. 10 моль одноатомного идеального газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (рис.1). Какое количество тепла получил газ на участке 2–3?

3. К источнику тока с ЭДС ε=9 В и внутренним сопротивлением r=1 Ом подключили параллельно соединенные резистор с сопротивлением R=8 Ом и плоский конденсатор, расстояние между пластинами которого d=0,002 м (рис.2). Какова напряженность электрического поля между пластинами конденсатора?

4. Проводящий стержень длиной L=10 см и сопротивлением R=1 Ом может скользить по горизонтально расположенным параллельным шинам, которые соединены с источником постоянного тока с ε=10 В и внутренним сопротивлением r=1 Ом (рис.3). К середине стержня прикреплена невесомая пружина с коэффициентом жесткости k=0,1 Н/м, расположенная в горизонтальной плоскости. Перпендикулярно плоскости проводников действует однородное магнитное поле с индукцией В=10^–2 Тл. Пренебрегая сопротивлением шин и проводов, определите энергию деформации пружины.

5. Точка движется по оси х по закону х =5+ 4t–2t² (м). Координата, в которой скорость точки обращается в нуль, равна…(м).