Лабораторная работа № 3. ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРОВ

ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРОВ

МЕТОДОМ БАЛЛИСТИЧЕСКОГО ГАЛЬВАНОМЕТРА

Принадлежности: баллистический гальванометр, измерительный стенд.

Краткая теория

Электроемкостью уединенного проводника называется способность накапливать заряд. Емкость численно равна величине заряда, изменяющего его потенциал на единицу:

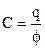(1)

Конденсаторы - это система двух тел, обладающая повышенной способностью конденсировать заряды. Емкость конденсатора определяется отношением:

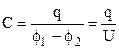(2)

Здесь 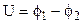- напряжение на пластинах плоского конденсатора. Следовательно, для измерения емкости необходимо измерять величину заряда и напряжение на конденсаторе. Заряд измеряется баллистическим гальванометром, напряжение – вольтметром

Емкость плоского конденсатора определяется выражением:

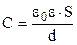(3)

где 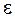- диэлектрическая проницаемость среды, S – площадь пластины, d - расстояние между пластинами конденсатора.

Емкость шара равна:

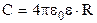(4)

где R – радиус шара.

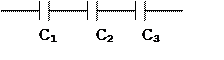При последовательном соединении конденсаторов

емкость определяется по формуле:

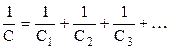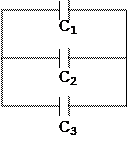При параллельном соединении конденсаторов

емкость определяется по формуле:

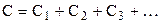
Баллистическим называется гальванометр, момент инерции подвижной части (рамки) которого специально увеличен. Если через гальванометр пропустить импульс тока (например, разрядить конденсатор) угол первого отброса рамки ( 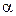) будет пропорционален заряду ( 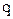), прошедшему через гальванометр:

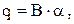
где В - баллистическая постоянная гальванометра.

В настоящей работе используется вспомогательный конденсатор известной емкости (эталон).

Для эталонного конденсатора 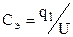, для исследуемого .

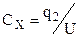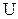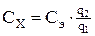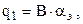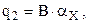Если напряжение ( ) одинаково, тo . Так как и то:

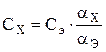(7)

Это выражение и определяет методику измерений.

Описание измерительной установки

В работе используется настольный баллистический гальванометр.

Измерительный стенд состоит из выпрямителя (рис. 1), вольтметра, эталонного ( 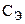) и исследуемого ( 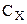) конденсаторов, двух переключателей, с помощью которых эталонный и исследуемый конденсаторы подключаются последовательно к выпрямителю для зарядки и к гальванометру для разряда.

Рис. 1

ПОРЯДОК ВЫПОЛНЕНИЯ

1. Изучить измерительную установку, записать величину .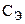

2. Собрать схему, включить стенд (тумблер "вкл"), включить подсветку шкалы гальванометра, установить шкалу на ноль.

3. Тумблер 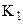установить в положение 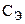, тумблер 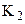в положение «выпр.».

4. Ручкой "регулировки 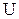" установить по вольтметру напряжение на конденсаторе 200 В и тумблером 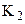разрядить 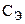на баллистический гальванометр (положение "Г"). Записать показания 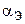, опыт повторить 3 раза.

5. Тумблером 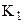подключить исследуемый конденсатор 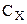к выпрямителю. Установить шкалу лимба 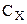на ноль и, произведя операцию по п. 4 записать показания 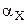. Затем, изменяя емкость 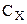с помощью переключателя на стенде, произвести измерения для каждого конденсатора.

Обработка результатов

1. Найти среднее значение .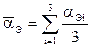

2. По формуле (3) рассчитать все измеренные значения .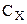

3. Рассчитать погрешность "калибровки" баллистического гальванометра и измерения .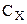

Таблица 1

	Сэ	С1	С2	С3	С4	С5	С6	С7	С8	С9	С10
α1
α2
α3
αср
Сx [пФ]

ПРЕДУПРЕЖДЕНИЕ: Не включайте цепь до ее проверки преподавателем или лаборантом. Можно испортить гальванометр!

Контрольные вопросы

1. Что называется электроемкостью? В каких единицах она измеряется в системах СИ и СГСЕ?

2. Как устроен и действует баллистический гальванометр?

3. Что измеряют (в нашей работе) баллистическим гальванометром?

4. Чему равна емкость шара, плоского конденсатора?

5. Как определяется емкость при последовательном и параллельном соединениях конденсаторов?

6. Какие вещества относят к диэлектрикам?

7. Что такое поляризация диэлектриков? Виды поляризации.

8. Каков физический смысл относительной диэлектрической постоянной.

9. Сформулируйте теорему Гаусса для электростатического поля в диэлектрике.

10. Что называется электрической индукцией? Как ведут себя линии электрической индукции на границе диэлектриков, вакуум-диэлектрик?

11. Энергия заряженного конденсатора.

Литература

1. Рублев Ю.В. и др. Практикум по электричеству, Высшая - школа, М.: 1971, стр. 227.

2. Конспект лекций.

Глава III

Постоянный ток

Электрический ток - это направленное перемещение зарядов. Сила тока 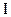измеряется величиной заряда, протекающего через поперечное сечение проводника за единицу времени:

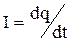(1)

За положительное направление тока принято направление движения положительных зарядов.

Экспериментальный закон Ома для участка цепи:

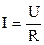(2)

где 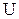- разность потенциалов (или падение напряжения) на концах участка цепи, сопротивление которого равно .

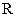Сопротивление проводников - это физическая величина, характеризующая тормозящее действие движению зарядов со стороны молекул проводника и определяемая зависимостью:

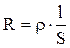(3)

где 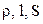- удельное сопротивление, длина и поперечное сечение проводника, соответственно. Из выражения (3) следует, что удельное сопротивление равно сопротивлению проводника единичной длины и сечения и определяется свойствами материала проводника (размерами молекул, плотностью упаковки, концентрацией и т.п.).

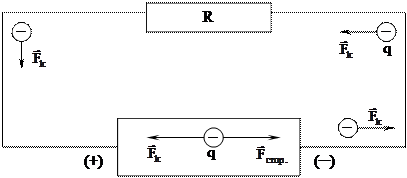
Перемещение зарядов (ток) под действием электрических сил в замкнутой цепи приводит к выравниванию зарядов по всей цепи. Следовательно, для поддержания тока постоянным в замкнутой цепи необходимо иметь участок, где происходит восстановление зарядов. На этом участке поля движение зарядов может осуществляться силами неэлектрической природы. Эти силы называются сторонними. Например, разделение зарядов происходит под действием химических сил в гальванических элементах, механических сил - в генераторах, тепловой энергии - в термоэлементах, световой энергии - в солнечных батареях.

Физическая величина, численно равная работе сторонних сил по перемещению единичного положительного заряда через всю цепь, называется электродвижущей силой (ЭДС):

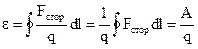(4)

Прибор, предназначенный для получения ЭДС называется источником тока.

В разомкнутой цепи электрические силы уравновешиваются сторонними и разность потенциалов на концах разомкнутого источника тока равна ЭДС.

Закон Ома для замкнутой цепи:

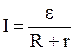(5)

где 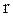- внутреннее сопротивление источника тока.

Для сложных электрических цепей применяются два закона Кирхгофа:

1. Алгебраическая сумма токов для любого узла цепи равна нулю:

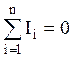(6)

2. Алгебраическая сумма падений напряжения в произвольном замкнутом контуре (выбранном в любой сложной цепи) равна алгебраической сумме ЭДС этого контура:

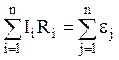(7)

Из формулы (4) следует, что полная работа, совершаемая сторонними силами в замкнутой цепи определяется зависимостью (закон Джоуля-Ленца):

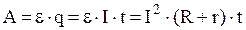(8)

Лабораторная работа № 4