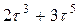Примеры выполнения тестовых заданий. Выполнение задания.Работа силы упругости равна убыли потенциальной энергии Wp и

Задание 1.Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания. На графике представлена зависимость проекции силы упругости пружины на положительное направление оси Х от координаты шарика. Работа силы упругости при смещении шарика из положения О в положение В равна … Дж.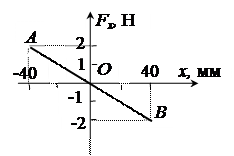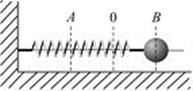
1)	-4·10-2	2)	4·10-2	3)	8·10-2	4)

Выполнение задания.Работа силы упругости равна убыли потенциальной энергии W_p и определяется формулой

.

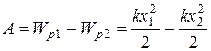С учетом условия задания (х₁ = 0, х₂ = 0,04 м) .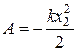

Сила упругости пружины равна 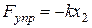, следовательно, окончательное выражение работы этой силы имеет вид 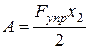. Вычислим: 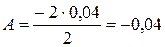(Дж).

Ответ: 1) -4·10^-2

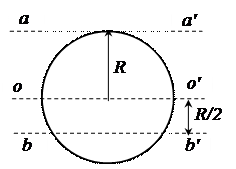
Задание 2.Шар массой m и радиусом R вращается около оси с постоянной угловой скоростью. Шар будет иметь большую кинетическую энергию, вращаясь около оси (см. рисунок) … 1) аа' 2) оо' 3) bb'

Выполнение задания. Кинетическая энергия вращательного движения равна

.

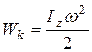Так как шар вращается с постоянной угловой скоростью ω, то кинетическая энергия зависит прямо пропорционально от момента инерции I_z относительно оси вращения. Момент инерции тела относительно произвольной оси определяется согласно теореме Штейнера и зависит от квадрата расстояния между осями d

.

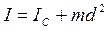Минимальный момент инерции шара относительно оси оо', так как ось проходит через центр масс шара. Наибольшее расстояние между осями оо' и аа', следовательно, и момент инерции относительно оси аа' максимальный, а значит и кинетическая энергия шара наибольшая при вращении около этой оси.

Ответ: 1) аа'

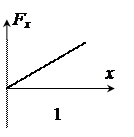
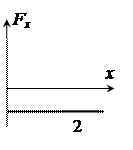
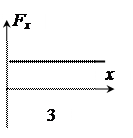
Задание 3.В потенциальном поле сила 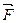пропорциональна градиенту потенциальной энергии Wp. Если график зависимости потенциальной энергии Wp от координаты х имеет вид, представленный на рисунке, то зависимость проекции силы Fx на ось Ох будет верна изображена на графике номер …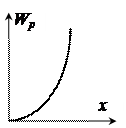

Выполнение задания. Зависимость проекции силы F_x на ось х от потенциальной энергии W_p определяется выражением

.

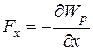Так как на представленном графике потенциальная энергия имеет квадратичную зависимость 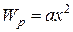, то, зависимость F_x = f(x) имеет следующий вид

/

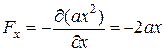Эта линейная зависимость представлена на рисунке под номером 4.

Ответ: 4)

Задание 4.Под действием силы 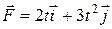тело движется со скоростью 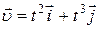. Мощность тела в момент времени t = τ равна …

1)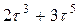

2)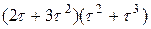

3)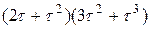

Выполнение задания.Мощность, развиваемая силой 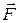, в данный момент времени t равна

.

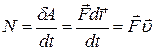Анализируя законы изменения силы 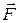и скорости 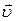, заданные координатно-векторным способом, определим их проекции на координатные оси: , , , .

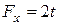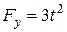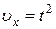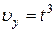Мощность – величина скалярная, следовательно, ее можно определить следующим образом

.

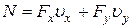После подстановки значений получим

.

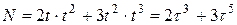Ответ: 1)