Вязкость (внутреннее трение). Закон Ньютона. Коэффициент вязкости
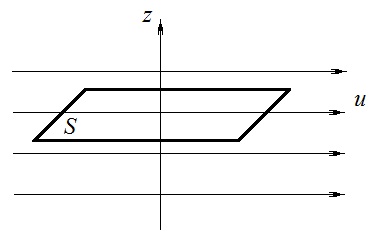
Вязкость (внутреннее трение) связано с возникновением сил трения между слоями газа (жидкости), перемешивающимися друг с другом с различными по модулю скоростями.
Со стороны слоя движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила и наоборот, медленно перемещающийся слой тормозит более быстро движущиеся слои газа (жидкости). Силы трения которые при этом возникают, направлены по касательной к поверхности соприкосновения слоев. С молекулярно-кинетической точки зрения причиной вязкости является упорядоченное движение слоев с различными скоростями u и хаотичного движения молекул υ.
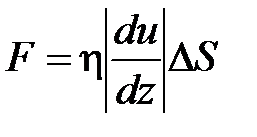 Согласно закону Ньютона сила трения между двумя слоями газа или жидкости равна.
Согласно закону Ньютона сила трения между двумя слоями газа или жидкости равна.
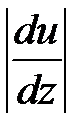 Эмпирическое уравнение вязкости, закон Ньютона:
Эмпирическое уравнение вязкости, закон Ньютона:
где η – коэффициент вязкости; - величина показывающая, как быстро изменяется
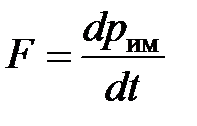 скорость течения жидкости или газа в направлении z, перпендикулярном к направлению движения слоев (градиент скорости u), S – площадь лежащей на границе между слоями поверхности, по которой действует сила F.
скорость течения жидкости или газа в направлении z, перпендикулярном к направлению движения слоев (градиент скорости u), S – площадь лежащей на границе между слоями поверхности, по которой действует сила F.
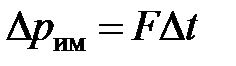
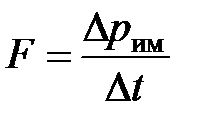 Согласно 2-му закону Ньютона:
Согласно 2-му закону Ньютона:
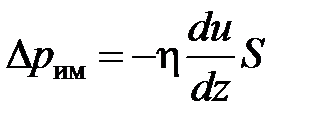 или, , тогда
или, , тогда
Уравнение Ньютона для внутреннего трения можно представить в виде:
где Δрим – импульс, передаваемый от слоя к слою за секунду (Δt=1 с), т.е. поток импульса через поверхность S. Знак «минус» в формуле обусловлен тем, что импульс «течет» в направлении убывания скорости u. Поэтому знаки импульса и градиента скорости u противоположны.
В формуле Ньютона минус писать нельзя, потому что она определяет одинаковый модуль двух противоположно направленных сил, с которыми слои действуют друг на друга. Кроме того нужно брать модуль градиента скорости, так как производная может иметь любой знак, а модуль силы – положительная величина.
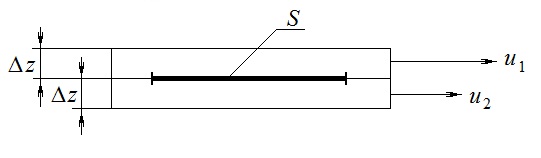
Рассмотрим происхождение силы внутреннего трения.
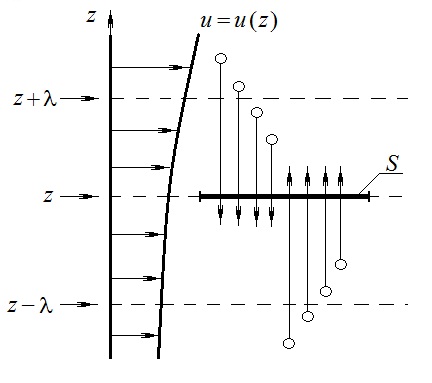
Рассмотрим два соприкасающихся слоя газа толщиной Δz. Слои движутся с различными скоростями u1 и u2. Каждая молекула газа участвует в двух движениях: хаотическом тепловом, средняя скорость которого равна <υ>, и упорядоченном движении со скоростью потока u. Скорость потока намного меньше, чем скорость теплового движения. В неподвижном газе средний импульс молекулы равен нулю. Молекула в потоке газа обладает средним импульсом mu. При рассмотрении внутреннего трениянас будет интересовать этот импульс.
Пусть в некоторый момент времени слои обладают импульсами рим1 и рим2. При отсутствии внешнего воздействия на слои, их импульсы не могут оставаться неизменными, так как вследствие теплового движения происходит непрерывный переход молекул из одного слоя в другой. Попав в другой слой, молекула претерпевает столкновения с молекулами этого слоя, в результате чего она отдает избыток своего импульса другим молекулам ( если она прилетела из слоя, движущегося быстрее), либо увеличивает свой импульс за счет других молекул (если она прилетела из слоя, движущегося медленнее). В итоге импульс слоя, движущегося быстрее, убывает, а слоя, движущегося медленнее, возрастает. Следовательно, слои ведут себя так, как если бы к слою, скорость которого больше, была приложена сила, тормозящая его движение, а к слою, скорость которого меньшая, - такая же по модулю сила, ускоряющая его движение. Таков механизм возникновения сил внутреннего трения.
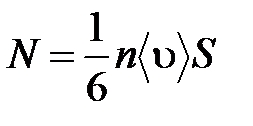 Через поверхность S, лежащую на границе раздела слоев, переходит в единицу времени из одного слоя в другой количество молекул, определяемое выражением:
Через поверхность S, лежащую на границе раздела слоев, переходит в единицу времени из одного слоя в другой количество молекул, определяемое выражением:
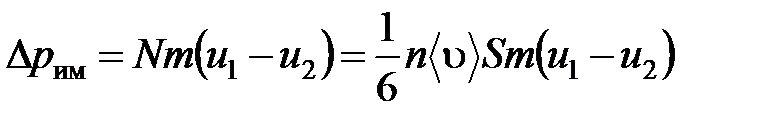 на среднюю скорость молекул в направлении, перпендикулярном к слоям, движение слоев со скоростью u не оказывает влияния). В результате возникает в направлении от более быстрого слоя к более медленному поток импульса через поверхность S, равный:
на среднюю скорость молекул в направлении, перпендикулярном к слоям, движение слоев со скоростью u не оказывает влияния). В результате возникает в направлении от более быстрого слоя к более медленному поток импульса через поверхность S, равный:
В реальном потоке газа скорость при переходе через воображаемую границу двух слоев изменяется не скачком, а непрерывно по закону u=u(z). Будем считать, что каждая молекула, пролетающая через поверхность S, несет с собой импульс mu, определяемый скоростью u в том месте, где произошло столкновение молекулы. Это столкновение происходит на различных расстояниях от S. В среднем последнее столкновение происходит на расстоянии, равном длине свободного пробега λ. Поэтому молекулам, летящим в направлении оси z, припишем значение скорости u1=u(z–λ), а молекулам, летящим в противоположном направлении, – значение скорости u2=u(z+λ). Подстановка этих значений в формулу для потока импульса через поверхность S в направлении оси z дает выражение:
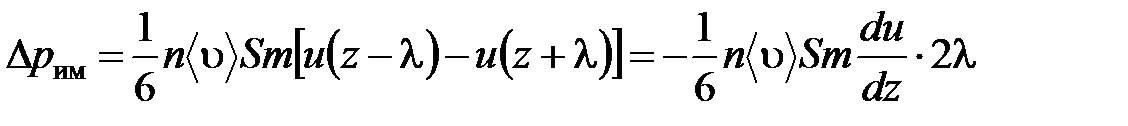
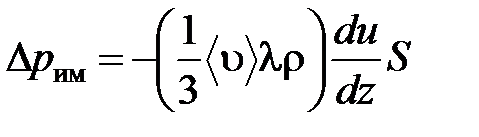 Произведение nm равно плотности газа ρ. Поэтому полученное уравнение можно записать в виде:
Произведение nm равно плотности газа ρ. Поэтому полученное уравнение можно записать в виде:
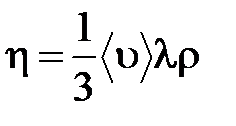 Сравнение полученного уравнения с эмпирической формулой Ньютона дает для вязкости выражение:
Сравнение полученного уравнения с эмпирической формулой Ньютона дает для вязкости выражение:
Размерность вязкости [η] = 1 (кг/(м∙с)) = 1 (Па∙с).
