Движение тел в жидкостях и газах

Одной из важнейших задач аэро- и гидродинамики является исследование движе­ния твердых тел в газе и жидкости, в частности изучение тех сил, с которыми среда действует на движущееся тело. а проблема приобрела особенно большое значение в связи с бурным развитием авиации и увеличением скорости движе­ния морских судов.

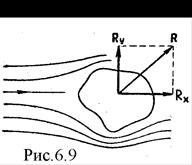
На тело, движущееся в жидкости или газе, действуют две силы (равнодействующую их обозначим 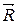), одна из которых ( 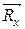) направлена в сторону, противопо­ложную движению тела (в сторону по­тока),- лобовое сопротивление,а вторая ( 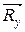) перпендикулярна этому направле­нию - подъемная сила(рис.6.9).

Если тело симметрично и его ось сим­метрии совпадает с направлением скоро­сти, то на него действует только лобовое сопротивление, подъемная же сила в этом случае равна нулю. Можно доказать, что в идеальной жидкости равномерное движение происходит без лобового сопро­тивления. Если рассмотреть движение ци­линдра в такой жидкости, то картина линий тока симметрична как от­носительно горизонтального, так и относительно вертикального направлений, т. е. ре­зультирующая сила давления на повер­хность цилиндра будет равна нулю.

Иначе обстоит дело при движении тел в вязкой жидкости (особенно при увеличе­нии скорости обтекания). Вследствие вяз­кости среды в области, прилегающей к по­верхности тела, образуется пограничный слой частиц, движущихся с меньшими ско­ростями. В результате тормозящего дейст­вия этого слоя возникает вращение частиц и движение жидкости в пограничном слое становится вихревым. Если тело не имеет обтекаемой формы (нет плавно утончаю­щейся хвостовой части), то пограничный слой жидкости отрывается от поверхности тела. За телом возникает течение жидко­сти (газа), направленное противоположно набегающему потоку. Оторвавшийся по граничный слой, следуя за этим течением, образует вихри, вращающиеся в противо­положные стороны (рис.6.10).

Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается безразмерным ко­эффициентом сопротивления С_x, определя­емым экспериментально:

R_x = C_x 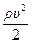S, (6.15)

где ρ- плотность среды; υ - скорость движения тела; S - наибольшее попере­чное сечение тела.

Составляющую R_x можно значитель­но уменьшить, подобрав тело такой фор­мы, которая не способствует образованию завихрения.

Подъемная сила может быть определе­на формулой, аналогичной (6.15):

R_y = C_y 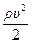S, (6.16)

где С_у - безразмерный коэффициент подъемной силы.

Основы молекулярной физики и термодинамики

ГЛАВА 7.ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-

КИНЕТИЧЕСКОЙ ТЕОРИИ

Введение

Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.

Идея об атомном строении вещества высказана древнегреческим философом Демокритом Атомистика возрождается в XVII в. и развивается в работах М. В. Ломоносова, взгляды которого на строение вещества и тепловые явления были близки к современным. Строгое развитие молекулярной теории относится к середине XIX в. и связано с работами немецкого физика Р. Клаузиуса, Дж. Максвелла и Л. Больцмана.

Процессы, изучаемые молекулярной физикой, являются результатом совместного действия большого числа молекул. Законы поведения огромного числа молекул изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы определяются свойствами частиц системы, особенностями их движения и усредненнымизначениями динамических характеристик этих частиц (скорости, энергии и т. д.). Например, температура тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена через среднее значение скорости молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул.

Температура — одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом. Температура – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Всоответствии с решением XI Генеральной конференции по мерам и весам в настоящее время можно применять только две температурные шкалы — термодинамическую и Международную практическую,градуированные соответственно в кельвинах (К) и в градусах Цельсия (°С). В Международной практической шкалетемпература замерзания и кипения воды при давлении 1,013· 10⁵ Па соответственно 0 и 100°С (реперныеточки).

Термодинамическая шкалаопределяется по одной реперной точке, в качестве которой взята тройная точка воды(температура, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии). Температура этой точки по термодинамической шкале равна 273,15 К. Градус Цельсия равен кельвину. В термодинамической шкале температура замерзания воды равна 273,15 К (при том же давлении, что и в Международной практической шкале), поэтому термодинамическая температура и температура по Международной практической шкале связаны соотношением

Т=273,15 + t.

Температура T=0 К называется нулем кельвин.Анализ различных процессов показывает, что 0 К недостижим, хотя приближение к нему сколь угодно близко возможно.

В молекулярно-кинетической теории пользуются идеализированной модельюидеального газа,согласно которой считают, что:

1) собственный объем молекул газа мал по сравнению с объемом сосуда;

2) между молекулами газа отсутствуют силы взаимодействия;

3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Модель идеального газа можно использовать при изучении реальных газов, так как они при нормальным условиях, а также при низких давлениях и высоких температурах, близки по своим свойствам к идеальному газу. Кроме того, внеся поправки, учитывающие собственный объем молекул газа и действующие молекулярные силы, можно перейти к теории реальных газов.