Измерение скорости потока и расхода жидкости

Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3), загнутый конец которой направлен навстречу потоку.

Трубка полного напора, или трубка Пито , служит для измерения скорости потока, например в трубе. Если установить в одном сечении потока трубку, изогнутую под углом 90, отверстием навстречу потоку и пьезометр, то жидкость в трубке поднимется над уровнем жидкости в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, следовательно, давление увеличивается на величину скоростного напора. Измерив, разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке.

Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

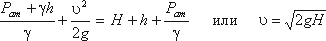
где Н - столб жидкости в трубке Пито.

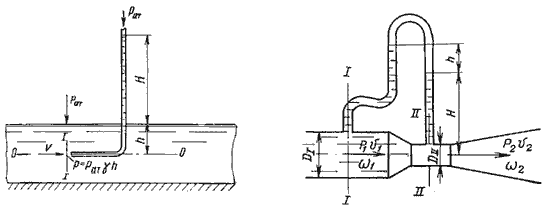
Рис. 3. Трубка Пито и pасходомер Вентури

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Расходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах и осуществляющее сужение потока – дросселирование. Расходомер состоит из двух участков – плавно сужающегося (сопла) и постепенно расширяющегося (диффузора). Скорость потока в сужающемся месте возрастает, а давление падает. Возникает разность (перепад) давлений, которую можно измерить двумя пьезометрами или дифференциальным U-образным ртутным манометром.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

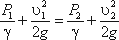
или

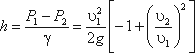
Используя уравнение неразрывности

Q = υ₁ω₁ = υ₂ω₂

сделаем замену в получено выражении:

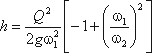
Решая относительно Q, получим

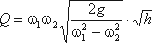
Выражение, стоящее перед 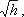, является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

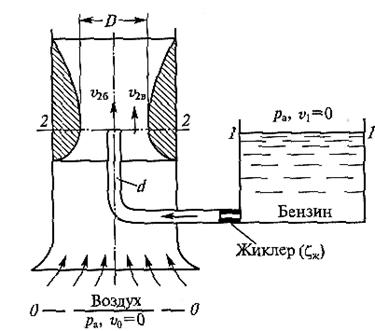
Карбюратор поршневых двигателей внутреннего сгорания (рис.4) служит для подсоса бензина и смешивания его с потоком воздуха. Поток воздуха, засасываемого в двигатель, сужается в том месте (сечение 2-2), где установлен распылитель бензина (обрез трубки диаметром d). Скорость воздуха в этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин вытекает в поток воздуха.

Рис. 4. Схема карбюратора

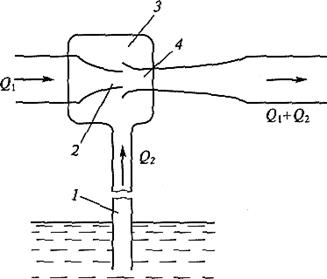Струйный насос (эжектор) (рис.5) состоит из плавно сходящегося насадка 2, осуществляющего сжатие потока, и постепенно расширяющейся трубки 4, установленной на некотором расстоянии от насадка в камере 3. Вследствие увеличения скорости потока давление в струе потока на выходе насадка 2 и во всей камере 3 значительно понижается. В расширяющейся трубке 4 скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу). Следовательно, в камере 3 давление обычно меньше атмосферного, т.е. в ней имеется разрежение (вакуум). Под действием разрежения жидкость из нижнего резервуара всасывается по трубе 1 в камеру 3, где происходит слияние и перемешивание двух потоков.

Рис. 5. Схема струйного насоса (эжектора):

1 — труба; 2 — насадок; 3 — камера; 4 — расширяющаяся трубка

Практическая работа №5.

Тема:Режимы движения жидкости.

Цель работы: Ознакомиться с режимами движения жидкости и опытом Рейнольдса.

Ход работы:

1. Записать определение ламинарного режима течения.

2. Записать определение турбулентного режима течения.

3. Зарисовать экспериментальную установку О.Рейнольдса и описать опыт.

4. Определить число Рейнольдса и режим движения воды в водопроводной трубе d мм, если расход воды Qм³/с.

Температура воды t⁰С.

5. Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр d_minмм максимальный диаметр d_maxмм. Расчётные скорости движения воды в них v₁…v₂ м/с. Определить минимальное и максимальное числа Рейнольдса и режим течения воды в этих трубопроводах.

Вариант	d мм	Qм3/с	t0С	dminмм	dmaxмм	v1 м/с	v2 м/с
1.		0,132				0,4	3,7
2.		0,134				0,5	3,8
3.		0,138				0,6	3,9
4.		0,132				0,7	4,0
5.		0,134				0,8	4,2
6.		0,138				0,4	4,3
7.		0,142				0,5	4,1
8.		0,132				0,6	4,5
9.		0,134				0,7	3,7
10.		0,138				0,8	3,8
11.		0,142				0,4	3,9
12.		0,132				0,5	4,0
13.		0,134				0,6	4,2
14.		0,138				0,7	4,3
Вариант		Qм3/с	t0С	dminмм	dmaxмм	v1 м/с	v2 м/с
15.		0,132				0,4	3,7
16.		0,134				0,5	3,8
17.		0,138				0,6	3,9
18.		0,142				0,7	4,0
19.		0,132				0,8	4,2
20.		0,134				0,4	4,3
21.		0,138				0,5	4,1
22.		0,142				0,6	4,5
23.		0,132				0,7	3,7
24.		0,134				0,8	3,8
25.		0,138				0,4	3,9
26.		0,142				0,5	4,0
27.		0,132				0,6	4,2
28.		0,134				0,7	4,3
29.		0,138				0,8	4,1
30.		0,142				0,4	4,5
31.		0,132				0,5	3,7

6. Вывод по работе.

Контрольные вопросы:

1. Дайте определение ламинарного режима течения.

2. Дайте определение турбулентного режима течения.

3. Перечислите факторы, от которых зависит характер течения жидкости.

4. В чем заключается физический смысл числа Рейнольдса.

5. Что означает критическое число Рейнольдс