7. Распределение Максвелла и Больцмана
| 1. Зависимость давления идеального газа во внешнем однородном поле силы тяжести от высоты для двух разных температур (Т2 > Т1) представлена на рисунке … | 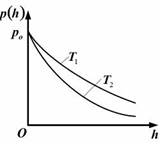 1. 1. 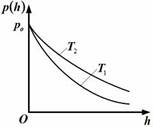 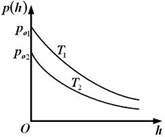  2. 3. 2. 3. 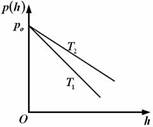 4. 4. |
Решение: 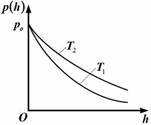 Зависимость давления идеального газа от высоты h для некоторой температуры T определяется барометрической формулой: Зависимость давления идеального газа от высоты h для некоторой температуры T определяется барометрической формулой: 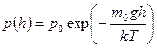 , где p0 – давление на высоте h = 0 , m0 – масса молекулы, g ускорение свободного падения, k постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура T. Давление p0 определяется весом всего газа и не меняется при изменении температуры. , где p0 – давление на высоте h = 0 , m0 – масса молекулы, g ускорение свободного падения, k постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура T. Давление p0 определяется весом всего газа и не меняется при изменении температуры. |
2. 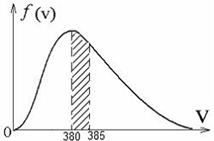 На рисунке представлен график функции распределения молекул кислорода по скоростям (распределение Максвелла) для температуры Т=273 К, при скорости 380 м/с функция достигает максимума. Здесь На рисунке представлен график функции распределения молекул кислорода по скоростям (распределение Максвелла) для температуры Т=273 К, при скорости 380 м/с функция достигает максимума. Здесь 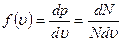 – плотность вероятности или доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. Для распределения Максвелла справедливы утверждения, что … – плотность вероятности или доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. Для распределения Максвелла справедливы утверждения, что … | Укажите не менее двух вариантов ответов 1.с понижением температуры площадь под кривой уменьшается  2.с ростом температуры наиболее вероятная скорость молекул увеличится 2.с ростом температуры наиболее вероятная скорость молекул увеличится  3.площадь заштрихованной полоски равна доле молекул со скоростями в интервале от υ1 = 380 м/с до υ2 = 385 м/с или вероятности того, что скорость молекулы имеет значение в этом интервале скоростей 4.отлична от нуля вероятность того, что молекула кислорода при Т = 273 К имеет скорость, точно равную 380 м/с 3.площадь заштрихованной полоски равна доле молекул со скоростями в интервале от υ1 = 380 м/с до υ2 = 385 м/с или вероятности того, что скорость молекулы имеет значение в этом интервале скоростей 4.отлична от нуля вероятность того, что молекула кислорода при Т = 273 К имеет скорость, точно равную 380 м/с |
Решение: 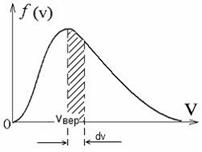 Функция распределения Максвелла Функция распределения Максвелла 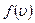 имеет смысл плотности вероятности имеет смысл плотности вероятности 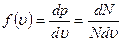 , где , где 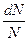 – доля молекул, скорости которых заключены в интервале от υ до υ + dυ. В нашем случае dυ = 5 м/с вблизи – доля молекул, скорости которых заключены в интервале от υ до υ + dυ. В нашем случае dυ = 5 м/с вблизи 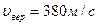 наиболее вероятной скорости молекул, близкой к которой движется большее число молекул. dN число молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с, N число всех молекул газа. Площадь заштрихованной полоски наиболее вероятной скорости молекул, близкой к которой движется большее число молекул. dN число молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с, N число всех молекул газа. Площадь заштрихованной полоски 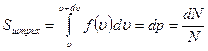 определяет долю молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с. С ростом температуры максимум кривой смещается вправо, высота максимума убывает. Наиболее вероятная скорость определяет долю молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с. С ростом температуры максимум кривой смещается вправо, высота максимума убывает. Наиболее вероятная скорость 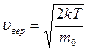 зависит от температуры газа: она увеличивается с повышением температуры. Вероятность того, что величина скорости может принять хотя бы какое-нибудь значение (достоверное событие), равна единице зависит от температуры газа: она увеличивается с повышением температуры. Вероятность того, что величина скорости может принять хотя бы какое-нибудь значение (достоверное событие), равна единице 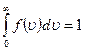 , поэтому при изменении температуры площадь под кривой остается равной единице. Если точно задана скорость υвер = 380,0 м/с, то dυ = 0, следовательно, вероятность dp = 0. , поэтому при изменении температуры площадь под кривой остается равной единице. Если точно задана скорость υвер = 380,0 м/с, то dυ = 0, следовательно, вероятность dp = 0. |
3. Формула Больцмана 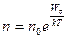 характеризует распределение частиц, находящихся в состоянии хаотического теплового движения, в потенциальном силовом поле, в частности распределение молекул по высоте в изотермической атмосфере. Соотнесите рисунки и соответствующие им утверждения. характеризует распределение частиц, находящихся в состоянии хаотического теплового движения, в потенциальном силовом поле, в частности распределение молекул по высоте в изотермической атмосфере. Соотнесите рисунки и соответствующие им утверждения. 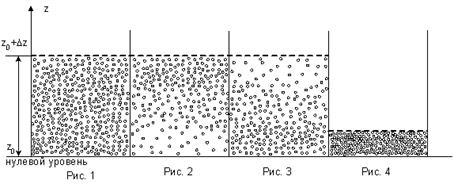 |
Установите соответствие (рис.4) 1.Распределение молекул в силовом поле при температуре 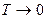 . 2.Распределение молекул по кинетическим энергиям. (рис.1) 3.Распределение молекул в силовом поле при очень высокой температуре, когда энергия хаотического теплового движения значительно превосходит потенциальную энергию молекул. (рис.2)4.Распределение молекул не является больцмановским и описывается функцией . 2.Распределение молекул по кинетическим энергиям. (рис.1) 3.Распределение молекул в силовом поле при очень высокой температуре, когда энергия хаотического теплового движения значительно превосходит потенциальную энергию молекул. (рис.2)4.Распределение молекул не является больцмановским и описывается функцией 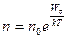 . (рис.3) 5.Распределение молекул воздуха в атмосфере Земли. . (рис.3) 5.Распределение молекул воздуха в атмосфере Земли. |
Решение: Концентрация молекул в однородном поле силы тяжести убывает с высотой по закону 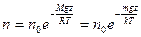 (распределение Больцмана на рис. 3), где n – концентрация молекул на высоте z, n0 – концентрация молекул на высоте z0 = 0, M молярная масса, m – масса молекулы, g – ускорение свободного падения, R – универсальная газовая постоянная, k – постоянная Больцмана, T – температура. В предельных случаях: если (распределение Больцмана на рис. 3), где n – концентрация молекул на высоте z, n0 – концентрация молекул на высоте z0 = 0, M молярная масса, m – масса молекулы, g – ускорение свободного падения, R – универсальная газовая постоянная, k – постоянная Больцмана, T – температура. В предельных случаях: если 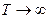 , то , то 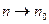 и молекулы равномерно распределяются по высоте (рис. 1); если и молекулы равномерно распределяются по высоте (рис. 1); если 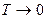 , то , то 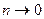 и молекулы располагаются на нулевом уровне (рис. 4). Если число молекул, имеющих большую потенциальную энергию, увеличивается по экспоненциальному закону и молекулы располагаются на нулевом уровне (рис. 4). Если число молекул, имеющих большую потенциальную энергию, увеличивается по экспоненциальному закону 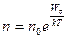 , то такое распределение можно назвать «антибольцмановским», или инверсным (рис. 2). , то такое распределение можно назвать «антибольцмановским», или инверсным (рис. 2). |
| 3. Зависимость концентрации молекул идеального газа во внешнем однородном поле силы тяжести от высоты для двух разных температур (Т2 > Т1) представлена на рисунке … | 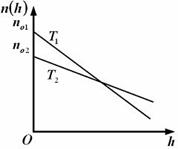 1. 2. 1. 2. 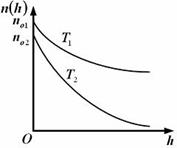 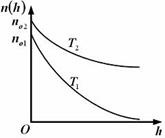 3. 3. 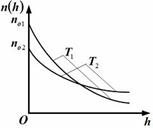  4. 4. |
Решение: Зависимость концентрации молекул идеального газа от высоты h для некоторой температуры T определяется распределением Больцмана: 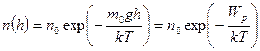 , где n0 – концентрация молекул на высоте h = 0, m0 – масса молекулы, g – ускорение свободного падения, k – постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул Wp, и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: Т2 > Т1. С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» (h = 0) уменьшается, а на высоте h увеличивается. , где n0 – концентрация молекул на высоте h = 0, m0 – масса молекулы, g – ускорение свободного падения, k – постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул Wp, и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: Т2 > Т1. С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» (h = 0) уменьшается, а на высоте h увеличивается. 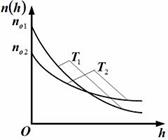 |
 4. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 4. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 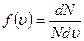 – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. Для этой функции является верным утверждение, что … – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. Для этой функции является верным утверждение, что … | 1. с увеличением температуры величина максимума функции увеличивается  2.при изменении температуры площадь под кривой не изменяется 3.при изменении температуры положение максимума не изменяется 4.с уменьшением температуры величина максимума функции уменьшается 2.при изменении температуры площадь под кривой не изменяется 3.при изменении температуры положение максимума не изменяется 4.с уменьшением температуры величина максимума функции уменьшается |
Решение: Полная вероятность равна: 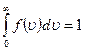 , т.е. площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости , т.е. площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 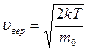 , при которой функция , при которой функция 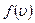 максимальна, следует, что при повышении температуры максимум функции сместится вправо. максимальна, следует, что при повышении температуры максимум функции сместится вправо. |
5. Внутренняя энергия молекулярного азота (газ считать идеальным) в результате процесса 1-2-3, изображенного на рисунке, изменяется на ___ Дж. 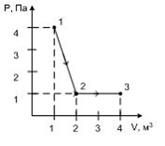 | 1.6 2. 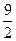 3. 4 4. 0 3. 4 4. 0 |
Решение: Изменение внутренней энергии как функции состояния не зависит от вида процесса, а определяется значением параметров газа в начальном и конечном состоянии. Следовательно, 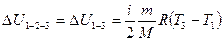 . Из диаграммы процесса видно, что . Из диаграммы процесса видно, что 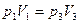 ; значит, ; значит, 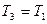 (точки 1 и 3 лежат на одной изотерме). Изменение внутренней энергии равно (точки 1 и 3 лежат на одной изотерме). Изменение внутренней энергии равно 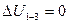 . . |
| 6. При увеличении давления в 3 раза и уменьшении объема в 2 раза внутренняя энергия идеального газа … |  1. увеличится в 1,5 раза 2.уменьшится в 1,5 раза 3. уменьшится в 6 раз 4. увеличится в 6 раз 1. увеличится в 1,5 раза 2.уменьшится в 1,5 раза 3. уменьшится в 6 раз 4. увеличится в 6 раз |
Решение: Внутренняя энергия идеального газа равна 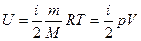 (учитываем, что (учитываем, что 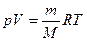 , где р – давление, V – объем, , где р – давление, V – объем, 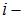 полное число степеней свободы, R – универсальная газовая постоянная, T – абсолютная температура, m – масса газа, M – молярная масса газа. полное число степеней свободы, R – универсальная газовая постоянная, T – абсолютная температура, m – масса газа, M – молярная масса газа. 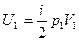 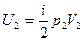 Учитывая, что Учитывая, что 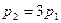 , , 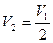 , получаем , получаем 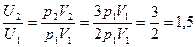 . Следовательно, . Следовательно, 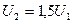 . . |
7. Идеальный газ имеет минимальную внутреннюю энергию в состоянии … 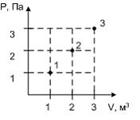 | 1.2 2.1,2,3 3.3  4.1 4.1 |
Решение: Внутренняя энергия идеального газа равна 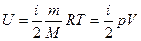 (учитываем, что (учитываем, что 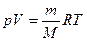 ), где р – давление, V – объем, i – полное число степеней свободы, R – универсальная газовая постоянная, T – абсолютная температура, m – масса газа, M – молярная масса газа. В нашем случае минимальное значение произведения ), где р – давление, V – объем, i – полное число степеней свободы, R – универсальная газовая постоянная, T – абсолютная температура, m – масса газа, M – молярная масса газа. В нашем случае минимальное значение произведения 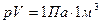 соответствует состоянию газа, обозначенному на p-V диаграмме точкой 1. Следовательно, идеальный газ имеет минимальную внутреннюю энергию в состоянии 1. соответствует состоянию газа, обозначенному на p-V диаграмме точкой 1. Следовательно, идеальный газ имеет минимальную внутреннюю энергию в состоянии 1. |
8.На рисунке представлены графики зависимости концентрации молекул идеального газа n от высоты h над уровнем моря для двух разны температур – Т1, Т2 (распределение Больцмана). 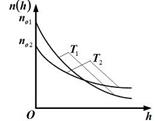 Для графиков этих функций верными являются утверждения, что … Для графиков этих функций верными являются утверждения, что … | Укажите не менее двух вариантов ответов  1. концентрация молекул газа на «нулевом уровне» (h = 0) с повышением температуры уменьшается 1. концентрация молекул газа на «нулевом уровне» (h = 0) с повышением температуры уменьшается  2. температура Т2 выше температуры Т1 3.температура Т2 ниже температуры Т1 4.концентрация молекул газа на «нулевом уровне» (h = 0) с повышением температуры увеличивается 2. температура Т2 выше температуры Т1 3.температура Т2 ниже температуры Т1 4.концентрация молекул газа на «нулевом уровне» (h = 0) с повышением температуры увеличивается |
9. Зависимость давления р идеального газа во внешнем однородном поле силы тяжести от высоты h для двух разных температур представлены на рисунке. 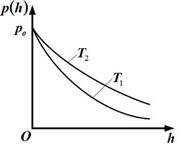 Для графиков этих функций невернымявляются утверждения, что … Для графиков этих функций невернымявляются утверждения, что … | Укажите не менее двух вариантов ответов 1. зависимость давления идеального газа от высоты определяется не только температурой газа, но и массой молекул 2.температура Т1 ниже температуры Т2  3.температура Т1 выше температуры Т2 3.температура Т1 выше температуры Т2  4.давление газа на высоте h равно давлению на «нулевом уровне» (h = 0), если температура газа стремится к абсолютному нулю 4.давление газа на высоте h равно давлению на «нулевом уровне» (h = 0), если температура газа стремится к абсолютному нулю |
10. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 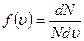 – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. 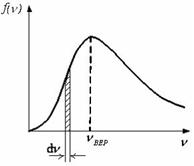 Для этой функции верными являются утверждения, что … Для этой функции верными являются утверждения, что … | Укажите не менее двух вариантов ответов 1. при изменении температуры положение максимума не изменяется 2. с увеличением температуры величина максимума функции увеличивается  3. при изменении температуры площадь под кривой не изменяется 3. при изменении температуры площадь под кривой не изменяется  4. с увеличением температуры максимум кривой смещается в право 4. с увеличением температуры максимум кривой смещается в право |
11. На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 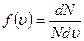 – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. 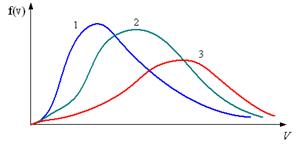 Для этой функции верными являются утверждения, что … Для этой функции верными являются утверждения, что … | Укажите не менее двух вариантов ответов 1. распределение 1 соответствует газу, имеющему наименьшую массу молекул  2. распределение 1 соответствует газу, имеющему наибольшую массу молекул 3.распределение 3 соответствует газу, имеющему наименьшую температуру 2. распределение 1 соответствует газу, имеющему наибольшую массу молекул 3.распределение 3 соответствует газу, имеющему наименьшую температуру  4. распределение 3 соответствует газу, имеющему наибольшую температуру 4. распределение 3 соответствует газу, имеющему наибольшую температуру |
12. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 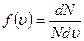 – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. 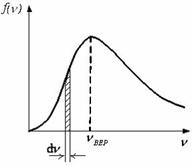 Для этой функции неверными являются утверждения, что … Для этой функции неверными являются утверждения, что … | Укажите не менее двух вариантов ответов 1. при понижении температуры площадь под кривой уменьшается 2. при понижении температуры величина максимума функции уменьшается 3. положение максимума кривой зависит не только от температуры, но и от природы газа 4. с ростом температуры наиболее вероятная скорость молекул увеличивается |
8. Средняя энергия молекул
1. Если не учитывать колебательные движения в линейной молекуле углекислого газа СО2 (см. рис.), то отношение кинетической энергии вращательного движения к полной кинетической энергии молекулы равно … 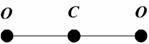 | 1. 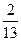 2. 2. 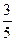 3. 3. 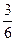  4. 4.  |
Решение: Средняя кинетическая энергия молекулы равна 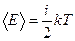 , где k – постоянная Больцмана, T – термодинамическая температура, i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: , где k – постоянная Больцмана, T – термодинамическая температура, i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: 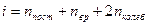 . Для линейной молекулы углекислого газа СО2 (см. рис.) число степеней свободы поступательного движения . Для линейной молекулы углекислого газа СО2 (см. рис.) число степеней свободы поступательного движения 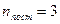 , вращательного – , вращательного – 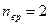 , колебательного – , колебательного – 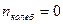 , поэтому i = 3 + 2 + 0 = 5. , поэтому i = 3 + 2 + 0 = 5. 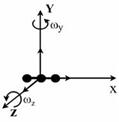 Следовательно, средняя кинетическая энергия молекулы СО2 равна Следовательно, средняя кинетическая энергия молекулы СО2 равна 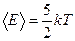 . Средняя энергия вращательного движения . Средняя энергия вращательного движения 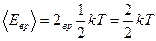 и составляет и составляет 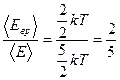 части от полной энергии. части от полной энергии. |
| 2. Кинетическая энергия вращательного движения всех молекул в 2 г водорода при температуре 100 К равна … | Введите ответ:  831 831 |
Решение: Средняя кинетическая энергия одной молекулы равна 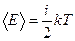 , где k – постоянная Больцмана, T – термодинамическая температура, i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы , где k – постоянная Больцмана, T – термодинамическая температура, i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы 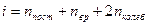 . Молекула водорода H2 имеет 2 вращательные степени свободы, следовательно, . Молекула водорода H2 имеет 2 вращательные степени свободы, следовательно, 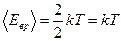 . В 2 г водорода содержится . В 2 г водорода содержится 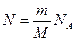 молекул, где m – масса газа, M – молярная масса водорода, NA – число Авогадро. Кинетическая энергия вращательного движения всех молекул будет равна: молекул, где m – масса газа, M – молярная масса водорода, NA – число Авогадро. Кинетическая энергия вращательного движения всех молекул будет равна: 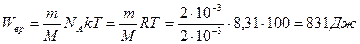 |
3. Из предложенных ниже идеальных газов выберите те, для которых отношение молярных теплоемкостей 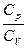 равно равно 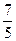 (колебаниями атомов внутри молекулы пренебречь). (колебаниями атомов внутри молекулы пренебречь). | Укажите не менее двух вариантов ответов 1. Водяной пар 2. Гелий  3. Воздух 3. Воздух  4. Кислород 4. Кислород |
Решение: 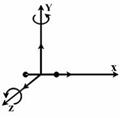 Из отношения Из отношения 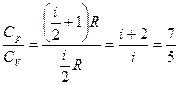 ; найдем сумму числа поступательных и числа вращательных степеней свободы молекулы i = 5, ; найдем сумму числа поступательных и числа вращательных степеней свободы молекулы i = 5, 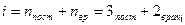 . На рисунке изображена модель молекулы газа, для которой выполняется последнее равенство. Прямыми стрелками показаны вероятные направления поступательного движения молекулы, круглыми – вращательного движения. Из предложенных газов этому условию удовлетворяет воздух, т.к. в этой смеси газов большую часть составляют двухатомные газы азот и кислород, и газ кислород. . На рисунке изображена модель молекулы газа, для которой выполняется последнее равенство. Прямыми стрелками показаны вероятные направления поступательного движения молекулы, круглыми – вращательного движения. Из предложенных газов этому условию удовлетворяет воздух, т.к. в этой смеси газов большую часть составляют двухатомные газы азот и кислород, и газ кислород. |
| 4. Средняя кинетическая энергия молекул газа при температуре Т зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место только поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекул азота (N2) равна … | 1. 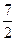  2. 2. 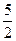 3. 3. 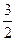 4. 4. 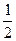 |
Решение: Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная 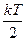 , а на каждую колебательную степень – kT. Средняя кинетическая энергия молекулы равна , а на каждую колебательную степень – kT. Средняя кинетическая энергия молекулы равна 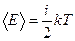 , где i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы. При условии, что имеют место только поступательное и вращательное движение, сумма числа степеней свободы равна , где i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы. При условии, что имеют место только поступательное и вращательное движение, сумма числа степеней свободы равна 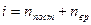 ; где ; где 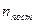 – число степеней свободы поступательного движения, равное – число степеней свободы поступательного движения, равное 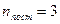 ; ; 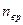 – число степеней свободы вращательного движения, которое может быть равно – число степеней свободы вращательного движения, которое может быть равно 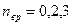 . Для молекулярного азота (двухатомной молекулы) . Для молекулярного азота (двухатомной молекулы) 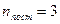 и и 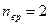 . Следовательно, i = 3 + 2 = 5 (3 степени свободы поступательного движения по направлениям осей ординат X, Y, Z и 2 степени свободы вращательного движения вокруг осей Y и Z) (см. рис.). Тогда средняя энергия молекул азота (N2) равна . Следовательно, i = 3 + 2 = 5 (3 степени свободы поступательного движения по направлениям осей ординат X, Y, Z и 2 степени свободы вращательного движения вокруг осей Y и Z) (см. рис.). Тогда средняя энергия молекул азота (N2) равна 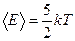 . . 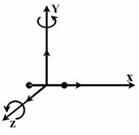 |
5. Молярная теплоемкость идеального газа при постоянном давлении равна 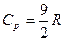 , где R = 8,31 Дж/(кг∙моль) – универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно … , где R = 8,31 Дж/(кг∙моль) – универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно … |  1. 2 2. 3 3.9 4.1 1. 2 2. 3 3.9 4.1 |
Решение: Молярные теплоемкости CV и Cp в изохорном и изобарном процессах соответственно равны: 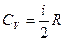 и и 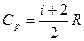 . Сравним: . Сравним: 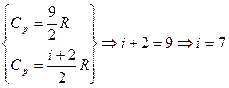 . Сумма числа степеней свободы i = 7 может быть представлена как . Сумма числа степеней свободы i = 7 может быть представлена как 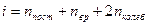 ; где ; где 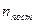 – число степеней свободы поступательного движения – число степеней свободы поступательного движения 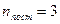 ; ; 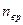 – число степеней свободы вращательного движения, которое может быть равно – число степеней свободы вращательного движения, которое может быть равно 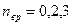 ; ; 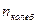 – число степеней свободы колебательного движения, минимальное количество которых равно 1 (см. рис.). – число степеней свободы колебательного движения, минимальное количество которых равно 1 (см. рис.). 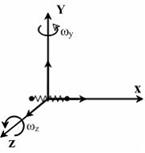 Следовательно, 7 = 3 + Следовательно, 7 = 3 + 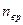 + 2 и + 2 и 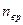 = 2. = 2. |
| 6. Изменение внутренней энергии газа при изохорном процессе возможно … | 1. в результате совершения газом работы 2. без теплообмена с внешней средой 3. в результате совершения внешними силами работы над газом  4.при теплообмене с внешней средой 4.при теплообмене с внешней средой |
Решение: Согласно первому началу термодинамики изменение внутренней энергии системы определяется формулой 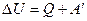 , где Q – количество теплоты, переданное системе внешней средой и не связанное с изменением объема; , где Q – количество теплоты, переданное системе внешней средой и не связанное с изменением объема; 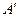 – работа, совершенная внешними телами над системой и связанная с изменением объема. Так как при изохорном процессе объем V = const то работа – работа, совершенная внешними телами над системой и связанная с изменением объема. Так как при изохорном процессе объем V = const то работа 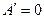 . Тогда первое начало термодинамики приобретает вид: . Тогда первое начало термодинамики приобретает вид: 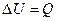 , т.е. изменение внутренней энергии возможно лишь при передаче газу теплоты извне (либо при передаче газом теплоты внешним телам). , т.е. изменение внутренней энергии возможно лишь при передаче газу теплоты извне (либо при передаче газом теплоты внешним телам). |
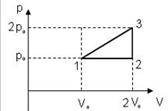 7. Идеальный газ переводят из состояния 1 в состояние 3 двумя способами: по пути 1-3 и 1-2-3. Отношение работ 7. Идеальный газ переводят из состояния 1 в состояние 3 двумя способами: по пути 1-3 и 1-2-3. Отношение работ 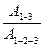 , совершенных газом, равно … , совершенных газом, равно … | 1.2  2. 1,5 3.3 4.4 2. 1,5 3.3 4.4 |
Решение: Работу газа можно найти как площадь под графиком процесса. В процессе 1-3 работа газа равна: 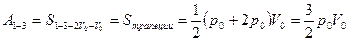 . С учетом того, что в изохорном процессе 2-3 газ работу не совершает . С учетом того, что в изохорном процессе 2-3 газ работу не совершает 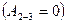 , имеем : , имеем : 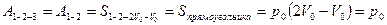 Отношение работ равно: Отношение работ равно: 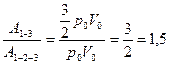 . . |
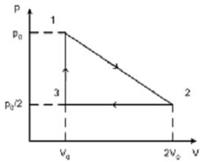 8. На рисунке изображен циклический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке… 8. На рисунке изображен циклический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке… | 1. 2-3  2. 1-2 3. 1-2, 2-3 4.3-1 2. 1-2 3. 1-2, 2-3 4.3-1 |
Решение: Из графика видно, что газ получает теплоту в процессах 1-2 и 3-1. Переход 3-1 осуществляется при постоянном объеме, следовательно, работа газа А3-1 = 0. Из графика видно, что точки 1 и 2 лежат на одной изотерме, т.к. 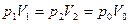 ; следовательно, Т1 = Т2 и изменение внутренней энергии ; следовательно, Т1 = Т2 и изменение внутренней энергии 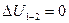 . По I началу термодинамики для процесса 1-2 количество теплоты равно: . По I началу термодинамики для процесса 1-2 количество теплоты равно: 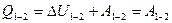 , т.е. газ совершает работу только за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде. , т.е. газ совершает работу только за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде. |
9. При комнатной температуре отношение 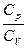 молярных теплоемкостей при постоянном давлении и постоянном объеме равно молярных теплоемкостей при постоянном давлении и постоянном объеме равно 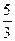 для … для … | 1. водяного пара 2. воздуха 3. кислорода  4. гелия 4. гелия |
10. В соответствии с законом распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре Т равна: 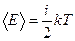 . Здесь . Здесь 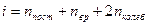 , где , где 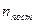 , , 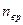 и и 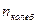 – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия (Не) число i равно … – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия (Не) число i равно … | 1. 5 2. 6  3. 3 4. 7 3. 3 4. 7 |
| 11. Средняя кинетическая энергия молекул газа при температуре Т зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, средняя кинетическая энергия молекулы кислорода (О2) равна … | 1. 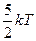 2. 2. 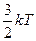 3. 3. 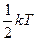  4. 4. 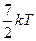 |
| 12. Кинетическая энергия (в Дж) всех молекул в 2 г неона при температуре 300 К равна … | 1.249  2. 374 3. 748 4. 831 2. 374 3. 748 4. 831 |
| 13. Если учитывать колебательное движение в молекуле водяного пара, то отношение кинетической энергии вращательного движения к полной кинетической энергии молекулы равно … | 1. 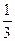 2. 2. 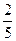 3. 3. 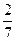  4. 4. 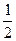 |
9. Второе начало термодинамики. Энтропия. Циклы.
| 1. КПД цикла Карно равен 40%. Если на 20% увеличить температуру нагревателя и на 20% уменьшить температуру охладителя, КПД (в % ) достигнет значения … | Введите ответ:  60 60 |
Решение: КПД обратимого цикла Карно равен: 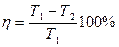 или или 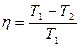 (в долях). После изменения температуры (в долях). После изменения температуры 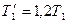 , , 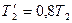 . . 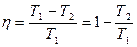 Первоначальный КПД равен, следовательно, Первоначальный КПД равен, следовательно, 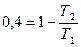 , отсюда , отсюда 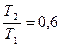 . После изменения . После изменения 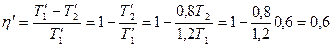 , , 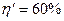 |
2. Адиабатному расширению газа (р – давление, V – объем, Т –температура, S – энтропия) соответствует диаграмма … 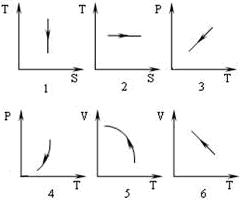 | Укажите не менее двух вариантов ответов 1.3 2.6 3.5 4.2  5.4 5.4  6.1 6.1 |
Решение: Для адиабатного процесса 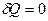 , тогда изменение энтропии системы , тогда изменение энтропии системы 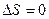 и и 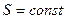 , т.к. , т.к. 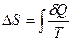 . Верным будет график 1. На графике 2 энтропия возрастает. Сравнивая графики 4 и 3, исключаем последний, т.к. он соответствует изохорному процессу. Для адиабатного процесса: . Верным будет график 1. На графике 2 энтропия возрастает. Сравнивая графики 4 и 3, исключаем последний, т.к. он соответствует изохорному процессу. Для адиабатного процесса: 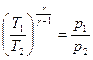 , где коэффициент Пуассона , где коэффициент Пуассона 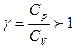 . Обозначив . Обозначив 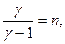 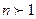 , получим , получим 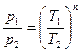 . Следовательно, p ~ Tn , график степенной функции изображен на рисунке 4. Для графиков 5 и 6 можно применить формулу . Следовательно, p ~ Tn , график степенной функции изображен на рисунке 4. Для графиков 5 и 6 можно применить формулу 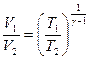 . Обозначив . Обозначив 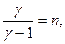 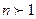 , получим , получим 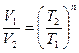 , т.е. V ~ , т.е. V ~ 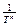 . График обратной степенной функции похож на график гиперболы. Следовательно, график 5 не отвечает адиабатному процессу, так же как и график 6. . График обратной степенной функции похож на график гиперболы. Следовательно, график 5 не отвечает адиабатному процессу, так же как и график 6. |
3. Чтобы расплавить некоторую массу меди, требуется большее количество теплоты, чем для плавления такой же массы цинка, так как удельная теплота плавления меди в 1,5 раза больше, чем цинка ( 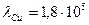 Дж/кг, Дж/кг, 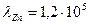 Дж/кг). Температура плавления меди примерно в 2 раза выше температуры плавления цинка ( Дж/кг). Температура плавления меди примерно в 2 раза выше температуры плавления цинка ( 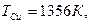 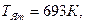 ). Разрушение кристаллической решетки металла при плавлении приводит к возрастанию энтропии. Если энтропия цинка увеличилась на ). Разрушение кристаллической решетки металла при плавлении приводит к возрастанию энтропии. Если энтропия цинка увеличилась на 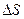 , то изменение энтропии меди составит … , то изменение энтропии меди составит … | 1. 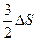 2. 2. 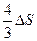  3. 3. 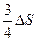 4. 4. 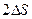 |
Решение: В термодинамике изменение энтропии определяется формулой 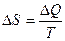 , где , где 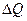 – количество теплоты, полученное системой при температуре Т. Пусть изменение энтропии при плавлении цинка – количество теплоты, полученное системой при температуре Т. Пусть изменение энтропии при плавлении цинка 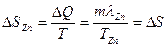 , тогда энтропия меди при ее плавлении возрастет на , тогда энтропия меди при ее плавлении возрастет на 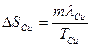 . Найдем отношение . Найдем отношение 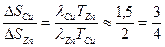 . Следовательно, . Следовательно, 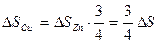 . . |
4. Уравнение кинетической теории для давления идеального газа имеет вид 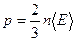 , где n – концентрация молекул. Для газа водорода , где n – концентрация молекул. Для газа водорода 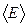 равно … равно … |  1. 1. 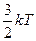 2. 2. 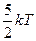 3. 3. 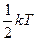 4. 4. 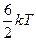 |
Решение: Давление газа обусловлено ударами молекул о стенку сосуда и определяется средним значением кинетической энергии поступательного движения молекул, а значит, поступательными степенями свободы 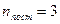 . Следовательно, . Следовательно, 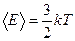 и не зависит от вида газа. и не зависит от вида газа. |
5. На каждую степень свободы движения молекулы приходится одинаковая энергия, равная 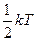 (k – постоянная Больцмана, T – температура по шкале Кельвина). Средняя кинетическая энергия атомарного водорода равна … (k – постоянная Больцмана, T – температура по шкале Кельвина). Средняя кинетическая энергия атомарного водорода равна … | 1. 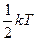  2. 2. 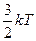 3. 3. 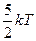 4. 4. 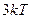 |
Решение: Средняя кинетическая энергия молекулы равна 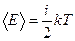 , где i – число степеней свободы молекулы. Атомарный водород – это одноатомный газ, атомы которого в данной модели участвуют только в поступательном движении , где i – число степеней свободы молекулы. Атомарный водород – это одноатомный газ, атомы которого в данной модели участвуют только в поступательном движении 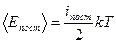 . Число степеней свободы . Число степеней свободы 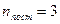 , т.к. положение центра инерции атома задается тремя координатами (x, y, z). Следовательно, , т.к. положение центра инерции атома задается тремя координатами (x, y, z). Следовательно, 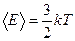 . . |
Наши рекомендации
 1.
1. 

 2. 3.
2. 3.  4.
4.  Зависимость давления идеального газа от высоты h для некоторой температуры T определяется барометрической формулой:
Зависимость давления идеального газа от высоты h для некоторой температуры T определяется барометрической формулой: 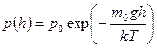 , где p0 – давление на высоте h = 0 , m0 – масса молекулы, g ускорение свободного падения, k постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура T. Давление p0 определяется весом всего газа и не меняется при изменении температуры.
, где p0 – давление на высоте h = 0 , m0 – масса молекулы, g ускорение свободного падения, k постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура T. Давление p0 определяется весом всего газа и не меняется при изменении температуры.  На рисунке представлен график функции распределения молекул кислорода по скоростям (распределение Максвелла) для температуры Т=273 К, при скорости 380 м/с функция достигает максимума. Здесь
На рисунке представлен график функции распределения молекул кислорода по скоростям (распределение Максвелла) для температуры Т=273 К, при скорости 380 м/с функция достигает максимума. Здесь 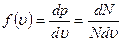 – плотность вероятности или доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. Для распределения Максвелла справедливы утверждения, что …
– плотность вероятности или доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. Для распределения Максвелла справедливы утверждения, что …  2.с ростом температуры наиболее вероятная скорость молекул увеличится
2.с ростом температуры наиболее вероятная скорость молекул увеличится  3.площадь заштрихованной полоски равна доле молекул со скоростями в интервале от υ1 = 380 м/с до υ2 = 385 м/с или вероятности того, что скорость молекулы имеет значение в этом интервале скоростей 4.отлична от нуля вероятность того, что молекула кислорода при Т = 273 К имеет скорость, точно равную 380 м/с
3.площадь заштрихованной полоски равна доле молекул со скоростями в интервале от υ1 = 380 м/с до υ2 = 385 м/с или вероятности того, что скорость молекулы имеет значение в этом интервале скоростей 4.отлична от нуля вероятность того, что молекула кислорода при Т = 273 К имеет скорость, точно равную 380 м/с  Функция распределения Максвелла
Функция распределения Максвелла 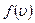 имеет смысл плотности вероятности
имеет смысл плотности вероятности 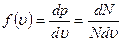 , где
, где 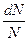 – доля молекул, скорости которых заключены в интервале от υ до υ + dυ. В нашем случае dυ = 5 м/с вблизи
– доля молекул, скорости которых заключены в интервале от υ до υ + dυ. В нашем случае dυ = 5 м/с вблизи 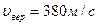 наиболее вероятной скорости молекул, близкой к которой движется большее число молекул. dN число молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с, N число всех молекул газа. Площадь заштрихованной полоски
наиболее вероятной скорости молекул, близкой к которой движется большее число молекул. dN число молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с, N число всех молекул газа. Площадь заштрихованной полоски 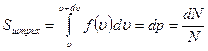 определяет долю молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с. С ростом температуры максимум кривой смещается вправо, высота максимума убывает. Наиболее вероятная скорость
определяет долю молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с. С ростом температуры максимум кривой смещается вправо, высота максимума убывает. Наиболее вероятная скорость 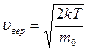 зависит от температуры газа: она увеличивается с повышением температуры. Вероятность того, что величина скорости может принять хотя бы какое-нибудь значение (достоверное событие), равна единице
зависит от температуры газа: она увеличивается с повышением температуры. Вероятность того, что величина скорости может принять хотя бы какое-нибудь значение (достоверное событие), равна единице 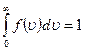 , поэтому при изменении температуры площадь под кривой остается равной единице. Если точно задана скорость υвер = 380,0 м/с, то dυ = 0, следовательно, вероятность dp = 0.
, поэтому при изменении температуры площадь под кривой остается равной единице. Если точно задана скорость υвер = 380,0 м/с, то dυ = 0, следовательно, вероятность dp = 0. 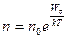 характеризует распределение частиц, находящихся в состоянии хаотического теплового движения, в потенциальном силовом поле, в частности распределение молекул по высоте в изотермической атмосфере. Соотнесите рисунки и соответствующие им утверждения.
характеризует распределение частиц, находящихся в состоянии хаотического теплового движения, в потенциальном силовом поле, в частности распределение молекул по высоте в изотермической атмосфере. Соотнесите рисунки и соответствующие им утверждения. 
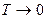 . 2.Распределение молекул по кинетическим энергиям. (рис.1) 3.Распределение молекул в силовом поле при очень высокой температуре, когда энергия хаотического теплового движения значительно превосходит потенциальную энергию молекул. (рис.2)4.Распределение молекул не является больцмановским и описывается функцией
. 2.Распределение молекул по кинетическим энергиям. (рис.1) 3.Распределение молекул в силовом поле при очень высокой температуре, когда энергия хаотического теплового движения значительно превосходит потенциальную энергию молекул. (рис.2)4.Распределение молекул не является больцмановским и описывается функцией 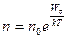 . (рис.3) 5.Распределение молекул воздуха в атмосфере Земли.
. (рис.3) 5.Распределение молекул воздуха в атмосфере Земли. 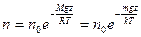 (распределение Больцмана на рис. 3), где n – концентрация молекул на высоте z, n0 – концентрация молекул на высоте z0 = 0, M молярная масса, m – масса молекулы, g – ускорение свободного падения, R – универсальная газовая постоянная, k – постоянная Больцмана, T – температура. В предельных случаях: если
(распределение Больцмана на рис. 3), где n – концентрация молекул на высоте z, n0 – концентрация молекул на высоте z0 = 0, M молярная масса, m – масса молекулы, g – ускорение свободного падения, R – универсальная газовая постоянная, k – постоянная Больцмана, T – температура. В предельных случаях: если 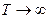 , то
, то 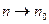 и молекулы равномерно распределяются по высоте (рис. 1); если
и молекулы равномерно распределяются по высоте (рис. 1); если 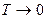 , то
, то 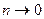 и молекулы располагаются на нулевом уровне (рис. 4). Если число молекул, имеющих большую потенциальную энергию, увеличивается по экспоненциальному закону
и молекулы располагаются на нулевом уровне (рис. 4). Если число молекул, имеющих большую потенциальную энергию, увеличивается по экспоненциальному закону 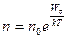 , то такое распределение можно назвать «антибольцмановским», или инверсным (рис. 2).
, то такое распределение можно назвать «антибольцмановским», или инверсным (рис. 2).  1. 2.
1. 2. 
 3.
3. 
 4.
4. 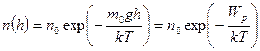 , где n0 – концентрация молекул на высоте h = 0, m0 – масса молекулы, g – ускорение свободного падения, k – постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул Wp, и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: Т2 > Т1. С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» (h = 0) уменьшается, а на высоте h увеличивается.
, где n0 – концентрация молекул на высоте h = 0, m0 – масса молекулы, g – ускорение свободного падения, k – постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул Wp, и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: Т2 > Т1. С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» (h = 0) уменьшается, а на высоте h увеличивается. 
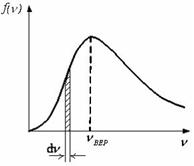
 4. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где
4. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 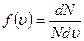 – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. Для этой функции является верным утверждение, что …
– доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала. Для этой функции является верным утверждение, что …  2.при изменении температуры площадь под кривой не изменяется 3.при изменении температуры положение максимума не изменяется 4.с уменьшением температуры величина максимума функции уменьшается
2.при изменении температуры площадь под кривой не изменяется 3.при изменении температуры положение максимума не изменяется 4.с уменьшением температуры величина максимума функции уменьшается 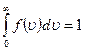 , т.е. площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
, т.е. площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 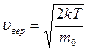 , при которой функция
, при которой функция 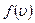 максимальна, следует, что при повышении температуры максимум функции сместится вправо.
максимальна, следует, что при повышении температуры максимум функции сместится вправо. 
 3. 4 4. 0
3. 4 4. 0 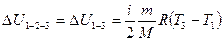 . Из диаграммы процесса видно, что
. Из диаграммы процесса видно, что 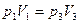 ; значит,
; значит, 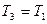 (точки 1 и 3 лежат на одной изотерме). Изменение внутренней энергии равно
(точки 1 и 3 лежат на одной изотерме). Изменение внутренней энергии равно 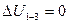 .
.  1. увеличится в 1,5 раза 2.уменьшится в 1,5 раза 3. уменьшится в 6 раз 4. увеличится в 6 раз
1. увеличится в 1,5 раза 2.уменьшится в 1,5 раза 3. уменьшится в 6 раз 4. увеличится в 6 раз 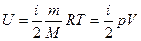 (учитываем, что
(учитываем, что 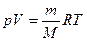 , где р – давление, V – объем,
, где р – давление, V – объем, 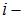 полное число степеней свободы, R – универсальная газовая постоянная, T – абсолютная температура, m – масса газа, M – молярная масса газа.
полное число степеней свободы, R – универсальная газовая постоянная, T – абсолютная температура, m – масса газа, M – молярная масса газа. 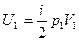
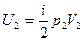 Учитывая, что
Учитывая, что 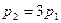 ,
, 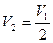 , получаем
, получаем 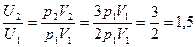 . Следовательно,
. Следовательно, 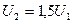 .
. 
 4.1
4.1 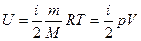 (учитываем, что
(учитываем, что 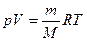 ), где р – давление, V – объем, i – полное число степеней свободы, R – универсальная газовая постоянная, T – абсолютная температура, m – масса газа, M – молярная масса газа. В нашем случае минимальное значение произведения
), где р – давление, V – объем, i – полное число степеней свободы, R – универсальная газовая постоянная, T – абсолютная температура, m – масса газа, M – молярная масса газа. В нашем случае минимальное значение произведения 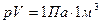 соответствует состоянию газа, обозначенному на p-V диаграмме точкой 1. Следовательно, идеальный газ имеет минимальную внутреннюю энергию в состоянии 1.
соответствует состоянию газа, обозначенному на p-V диаграмме точкой 1. Следовательно, идеальный газ имеет минимальную внутреннюю энергию в состоянии 1.  Для графиков этих функций верными являются утверждения, что …
Для графиков этих функций верными являются утверждения, что …  1. концентрация молекул газа на «нулевом уровне» (h = 0) с повышением температуры уменьшается
1. концентрация молекул газа на «нулевом уровне» (h = 0) с повышением температуры уменьшается  2. температура Т2 выше температуры Т1 3.температура Т2 ниже температуры Т1 4.концентрация молекул газа на «нулевом уровне» (h = 0) с повышением температуры увеличивается
2. температура Т2 выше температуры Т1 3.температура Т2 ниже температуры Т1 4.концентрация молекул газа на «нулевом уровне» (h = 0) с повышением температуры увеличивается  Для графиков этих функций невернымявляются утверждения, что …
Для графиков этих функций невернымявляются утверждения, что …  3.температура Т1 выше температуры Т2
3.температура Т1 выше температуры Т2  4.давление газа на высоте h равно давлению на «нулевом уровне» (h = 0), если температура газа стремится к абсолютному нулю
4.давление газа на высоте h равно давлению на «нулевом уровне» (h = 0), если температура газа стремится к абсолютному нулю 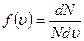 – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала.
– доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала.  Для этой функции верными являются утверждения, что …
Для этой функции верными являются утверждения, что …  3. при изменении температуры площадь под кривой не изменяется
3. при изменении температуры площадь под кривой не изменяется  4. с увеличением температуры максимум кривой смещается в право
4. с увеличением температуры максимум кривой смещается в право 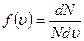 – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала.
– доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала.  Для этой функции верными являются утверждения, что …
Для этой функции верными являются утверждения, что …  2. распределение 1 соответствует газу, имеющему наибольшую массу молекул 3.распределение 3 соответствует газу, имеющему наименьшую температуру
2. распределение 1 соответствует газу, имеющему наибольшую массу молекул 3.распределение 3 соответствует газу, имеющему наименьшую температуру  4. распределение 3 соответствует газу, имеющему наибольшую температуру
4. распределение 3 соответствует газу, имеющему наибольшую температуру 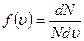 – доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала.
– доля молекул, скорости которых заключены в интервале скоростей от υ до υ + dυ в расчете на единицу этого интервала.  Для этой функции неверными являются утверждения, что …
Для этой функции неверными являются утверждения, что … 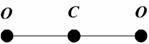
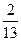 2.
2. 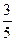 3.
3. 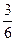
 4.
4. 
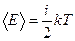 , где k – постоянная Больцмана, T – термодинамическая температура, i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы:
, где k – постоянная Больцмана, T – термодинамическая температура, i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: 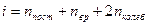 . Для линейной молекулы углекислого газа СО2 (см. рис.) число степеней свободы поступательного движения
. Для линейной молекулы углекислого газа СО2 (см. рис.) число степеней свободы поступательного движения 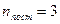 , вращательного –
, вращательного – 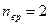 , колебательного –
, колебательного – 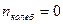 , поэтому i = 3 + 2 + 0 = 5.
, поэтому i = 3 + 2 + 0 = 5.  Следовательно, средняя кинетическая энергия молекулы СО2 равна
Следовательно, средняя кинетическая энергия молекулы СО2 равна 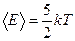 . Средняя энергия вращательного движения
. Средняя энергия вращательного движения 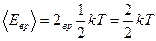 и составляет
и составляет 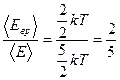 части от полной энергии.
части от полной энергии.  831
831 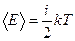 , где k – постоянная Больцмана, T – термодинамическая температура, i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы
, где k – постоянная Больцмана, T – термодинамическая температура, i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы 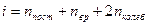 . Молекула водорода H2 имеет 2 вращательные степени свободы, следовательно,
. Молекула водорода H2 имеет 2 вращательные степени свободы, следовательно, 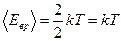 . В 2 г водорода содержится
. В 2 г водорода содержится 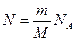 молекул, где m – масса газа, M – молярная масса водорода, NA – число Авогадро. Кинетическая энергия вращательного движения всех молекул будет равна:
молекул, где m – масса газа, M – молярная масса водорода, NA – число Авогадро. Кинетическая энергия вращательного движения всех молекул будет равна: 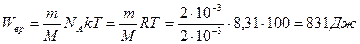
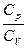 равно
равно 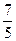 (колебаниями атомов внутри молекулы пренебречь).
(колебаниями атомов внутри молекулы пренебречь).  3. Воздух
3. Воздух  4. Кислород
4. Кислород  Из отношения
Из отношения 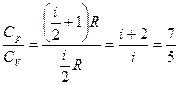 ; найдем сумму числа поступательных и числа вращательных степеней свободы молекулы i = 5,
; найдем сумму числа поступательных и числа вращательных степеней свободы молекулы i = 5, 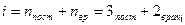 . На рисунке изображена модель молекулы газа, для которой выполняется последнее равенство. Прямыми стрелками показаны вероятные направления поступательного движения молекулы, круглыми – вращательного движения. Из предложенных газов этому условию удовлетворяет воздух, т.к. в этой смеси газов большую часть составляют двухатомные газы азот и кислород, и газ кислород.
. На рисунке изображена модель молекулы газа, для которой выполняется последнее равенство. Прямыми стрелками показаны вероятные направления поступательного движения молекулы, круглыми – вращательного движения. Из предложенных газов этому условию удовлетворяет воздух, т.к. в этой смеси газов большую часть составляют двухатомные газы азот и кислород, и газ кислород. 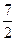
 2.
2. 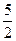 3.
3. 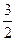 4.
4. 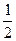
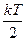 , а на каждую колебательную степень – kT. Средняя кинетическая энергия молекулы равна
, а на каждую колебательную степень – kT. Средняя кинетическая энергия молекулы равна 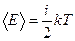 , где i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы. При условии, что имеют место только поступательное и вращательное движение, сумма числа степеней свободы равна
, где i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы. При условии, что имеют место только поступательное и вращательное движение, сумма числа степеней свободы равна 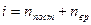 ; где
; где 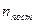 – число степеней свободы поступательного движения, равное
– число степеней свободы поступательного движения, равное 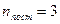 ;
; 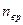 – число степеней свободы вращательного движения, которое может быть равно
– число степеней свободы вращательного движения, которое может быть равно 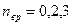 . Для молекулярного азота (двухатомной молекулы)
. Для молекулярного азота (двухатомной молекулы) 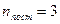 и
и 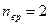 . Следовательно, i = 3 + 2 = 5 (3 степени свободы поступательного движения по направлениям осей ординат X, Y, Z и 2 степени свободы вращательного движения вокруг осей Y и Z) (см. рис.). Тогда средняя энергия молекул азота (N2) равна
. Следовательно, i = 3 + 2 = 5 (3 степени свободы поступательного движения по направлениям осей ординат X, Y, Z и 2 степени свободы вращательного движения вокруг осей Y и Z) (см. рис.). Тогда средняя энергия молекул азота (N2) равна 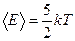 .
. 
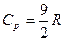 , где R = 8,31 Дж/(кг∙моль) – универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно …
, где R = 8,31 Дж/(кг∙моль) – универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно …  1. 2 2. 3 3.9 4.1
1. 2 2. 3 3.9 4.1 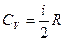 и
и 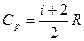 . Сравним:
. Сравним: 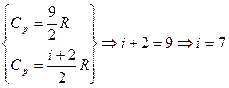 . Сумма числа степеней свободы i = 7 может быть представлена как
. Сумма числа степеней свободы i = 7 может быть представлена как 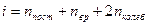 ; где
; где 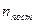 – число степеней свободы поступательного движения
– число степеней свободы поступательного движения 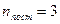 ;
; 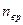 – число степеней свободы вращательного движения, которое может быть равно
– число степеней свободы вращательного движения, которое может быть равно 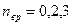 ;
; 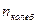 – число степеней свободы колебательного движения, минимальное количество которых равно 1 (см. рис.).
– число степеней свободы колебательного движения, минимальное количество которых равно 1 (см. рис.).  Следовательно, 7 = 3 +
Следовательно, 7 = 3 + 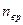 + 2 и
+ 2 и 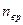 = 2.
= 2.  4.при теплообмене с внешней средой
4.при теплообмене с внешней средой 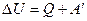 , где Q – количество теплоты, переданное системе внешней средой и не связанное с изменением объема;
, где Q – количество теплоты, переданное системе внешней средой и не связанное с изменением объема; 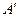 – работа, совершенная внешними телами над системой и связанная с изменением объема. Так как при изохорном процессе объем V = const то работа
– работа, совершенная внешними телами над системой и связанная с изменением объема. Так как при изохорном процессе объем V = const то работа 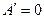 . Тогда первое начало термодинамики приобретает вид:
. Тогда первое начало термодинамики приобретает вид: 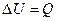 , т.е. изменение внутренней энергии возможно лишь при передаче газу теплоты извне (либо при передаче газом теплоты внешним телам).
, т.е. изменение внутренней энергии возможно лишь при передаче газу теплоты извне (либо при передаче газом теплоты внешним телам).  7. Идеальный газ переводят из состояния 1 в состояние 3 двумя способами: по пути 1-3 и 1-2-3. Отношение работ
7. Идеальный газ переводят из состояния 1 в состояние 3 двумя способами: по пути 1-3 и 1-2-3. Отношение работ 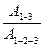 , совершенных газом, равно …
, совершенных газом, равно …  2. 1,5 3.3 4.4
2. 1,5 3.3 4.4 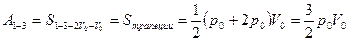 . С учетом того, что в изохорном процессе 2-3 газ работу не совершает
. С учетом того, что в изохорном процессе 2-3 газ работу не совершает 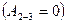 , имеем :
, имеем : 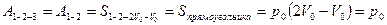 Отношение работ равно:
Отношение работ равно: 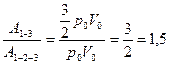 .
.  8. На рисунке изображен циклический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке…
8. На рисунке изображен циклический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке…  2. 1-2 3. 1-2, 2-3 4.3-1
2. 1-2 3. 1-2, 2-3 4.3-1 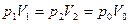 ; следовательно, Т1 = Т2 и изменение внутренней энергии
; следовательно, Т1 = Т2 и изменение внутренней энергии 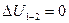 . По I началу термодинамики для процесса 1-2 количество теплоты равно:
. По I началу термодинамики для процесса 1-2 количество теплоты равно: 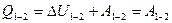 , т.е. газ совершает работу только за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде.
, т.е. газ совершает работу только за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде. 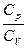 молярных теплоемкостей при постоянном давлении и постоянном объеме равно
молярных теплоемкостей при постоянном давлении и постоянном объеме равно 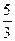 для …
для …  4. гелия
4. гелия 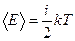 . Здесь
. Здесь 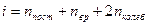 , где
, где 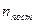 ,
, 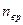 и
и 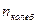 – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия (Не) число i равно …
– число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия (Не) число i равно …  3. 3 4. 7
3. 3 4. 7 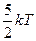 2.
2. 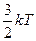 3.
3. 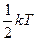
 4.
4. 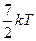
 2. 374 3. 748 4. 831
2. 374 3. 748 4. 831 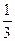 2.
2. 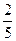 3.
3. 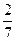
 4.
4. 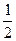
 60
60 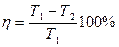 или
или 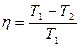 (в долях). После изменения температуры
(в долях). После изменения температуры 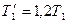 ,
, 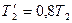 .
. 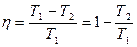 Первоначальный КПД равен, следовательно,
Первоначальный КПД равен, следовательно, 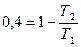 , отсюда
, отсюда 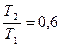 . После изменения
. После изменения 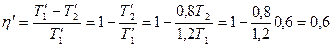 ,
, 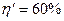

 5.4
5.4  6.1
6.1 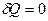 , тогда изменение энтропии системы
, тогда изменение энтропии системы 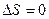 и
и 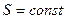 , т.к.
, т.к. 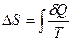 . Верным будет график 1. На графике 2 энтропия возрастает. Сравнивая графики 4 и 3, исключаем последний, т.к. он соответствует изохорному процессу. Для адиабатного процесса:
. Верным будет график 1. На графике 2 энтропия возрастает. Сравнивая графики 4 и 3, исключаем последний, т.к. он соответствует изохорному процессу. Для адиабатного процесса: 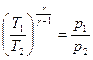 , где коэффициент Пуассона
, где коэффициент Пуассона 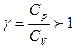 . Обозначив
. Обозначив 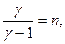
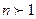 , получим
, получим 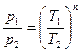 . Следовательно, p ~ Tn , график степенной функции изображен на рисунке 4. Для графиков 5 и 6 можно применить формулу
. Следовательно, p ~ Tn , график степенной функции изображен на рисунке 4. Для графиков 5 и 6 можно применить формулу 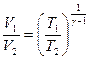 . Обозначив
. Обозначив 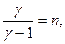
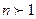 , получим
, получим 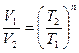 , т.е. V ~
, т.е. V ~ 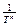 . График обратной степенной функции похож на график гиперболы. Следовательно, график 5 не отвечает адиабатному процессу, так же как и график 6.
. График обратной степенной функции похож на график гиперболы. Следовательно, график 5 не отвечает адиабатному процессу, так же как и график 6. 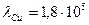 Дж/кг,
Дж/кг, 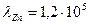 Дж/кг). Температура плавления меди примерно в 2 раза выше температуры плавления цинка (
Дж/кг). Температура плавления меди примерно в 2 раза выше температуры плавления цинка ( 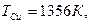
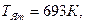 ). Разрушение кристаллической решетки металла при плавлении приводит к возрастанию энтропии. Если энтропия цинка увеличилась на
). Разрушение кристаллической решетки металла при плавлении приводит к возрастанию энтропии. Если энтропия цинка увеличилась на 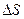 , то изменение энтропии меди составит …
, то изменение энтропии меди составит … 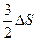 2.
2. 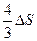
 3.
3. 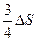 4.
4. 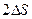
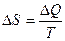 , где
, где 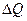 – количество теплоты, полученное системой при температуре Т. Пусть изменение энтропии при плавлении цинка
– количество теплоты, полученное системой при температуре Т. Пусть изменение энтропии при плавлении цинка 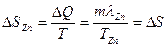 , тогда энтропия меди при ее плавлении возрастет на
, тогда энтропия меди при ее плавлении возрастет на 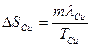 . Найдем отношение
. Найдем отношение 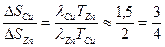 . Следовательно,
. Следовательно, 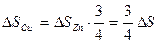 .
. 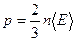 , где n – концентрация молекул. Для газа водорода
, где n – концентрация молекул. Для газа водорода 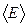 равно …
равно …  1.
1. 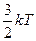 2.
2. 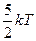 3.
3. 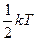 4.
4. 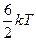
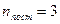 . Следовательно,
. Следовательно, 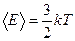 и не зависит от вида газа.
и не зависит от вида газа. 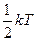 (k – постоянная Больцмана, T – температура по шкале Кельвина). Средняя кинетическая энергия атомарного водорода равна …
(k – постоянная Больцмана, T – температура по шкале Кельвина). Средняя кинетическая энергия атомарного водорода равна … 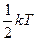
 2.
2. 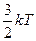 3.
3. 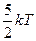 4.
4. 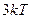
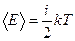 , где i – число степеней свободы молекулы. Атомарный водород – это одноатомный газ, атомы которого в данной модели участвуют только в поступательном движении
, где i – число степеней свободы молекулы. Атомарный водород – это одноатомный газ, атомы которого в данной модели участвуют только в поступательном движении 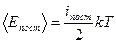 . Число степеней свободы
. Число степеней свободы 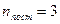 , т.к. положение центра инерции атома задается тремя координатами (x, y, z). Следовательно,
, т.к. положение центра инерции атома задается тремя координатами (x, y, z). Следовательно, 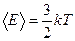 .
. 