Магнитное поле прямолинейного проводника с током
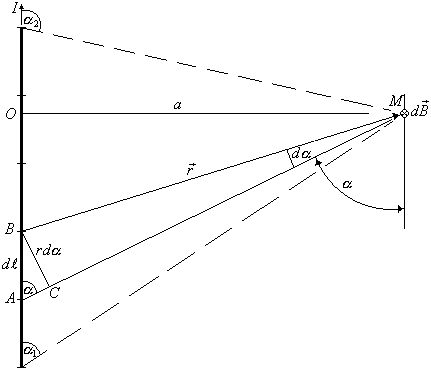
Вычислим индукцию магнитного поля, создаваемого прямолинейным проводником с током в произвольной точке М. Мысленно разобьем проводник на элементарно малые участки длиною 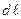 . Согласно правилу буравчика в точке М векторы
. Согласно правилу буравчика в точке М векторы 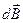 от всех элементов тока имеют одинаковое направление — за плоскость рисунка. Поэтому сложение векторов
от всех элементов тока имеют одинаковое направление — за плоскость рисунка. Поэтому сложение векторов 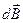 можно заменить сложением их модулей
можно заменить сложением их модулей 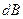 , причем
, причем
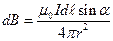 . (3)
. (3)
Для интегрирования нужно переменные 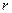 ,
, 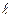 , и
, и 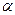 выразить через одну какую-либо из них. В качестве переменной интегрирования выберем угол
выразить через одну какую-либо из них. В качестве переменной интегрирования выберем угол 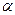 . ВС — есть дуга окружности радиуса r с центром в точке
. ВС — есть дуга окружности радиуса r с центром в точке 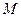 , равная
, равная 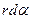 (см. рисунок). Выразим
(см. рисунок). Выразим 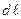 из прямоугольного треугольника АВС:
из прямоугольного треугольника АВС: 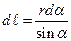 . Подставив это выражение в (3) получим
. Подставив это выражение в (3) получим 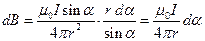 . Из треугольника АОМ определим
. Из треугольника АОМ определим 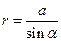 , где
, где 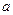 — кратчайшее расстояние от точки поля
— кратчайшее расстояние от точки поля 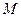 до линии тока. Тогда
до линии тока. Тогда
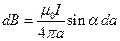 .
.
Интегрируя последнее выражение по всем элементам тока, что эквивалентно интегрированию от 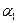 до
до  , находим
, находим 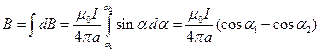 .
.
Таким образом, индукция магнитного поля, созданного прямолинейным током конечной длины будет равна
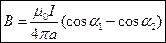 .
.
В дальнейшем, я введу понятие вектора напряженности магнитного поля 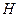 , которое связано с индукцией магнитного поля соотношением
, которое связано с индукцией магнитного поля соотношением 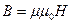 ,
, 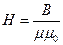 , где
, где 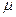 — магнитная проницаемость среды. Для вакуума
— магнитная проницаемость среды. Для вакуума 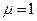 , для воздуха
, для воздуха 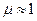 . Тогда напряженность магнитного поля, созданного проводником конечной длины будет равна
. Тогда напряженность магнитного поля, созданного проводником конечной длины будет равна
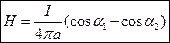 .
.
Для прямолинейного проводника бесконечной длины углы 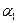 и
и  будут равны
будут равны 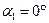 ,
, 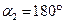 , а выражение в скобках принимает значение
, а выражение в скобках принимает значение 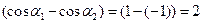 . Следовательно, индукция и напряженность магнитного поля, созданного прямолинейным проводником с током бесконечной длины равны соответственно
. Следовательно, индукция и напряженность магнитного поля, созданного прямолинейным проводником с током бесконечной длины равны соответственно
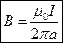 ,
, 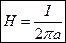 .
.
Магнитное поле кругового тока
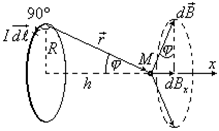 |
В качестве второго применения закона Био — Савара — Лапласа вычислим индукцию и напряженность магнитного поля на оси кругового тока. Обозначим радиус окружности проводника с током через 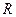 , расстояние от центра кругового тока до исследуемой точки поля
, расстояние от центра кругового тока до исследуемой точки поля 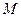 через h. От всех элементов тока образуется конус векторов
через h. От всех элементов тока образуется конус векторов 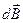 , и легко сообразить, что результирующий вектор
, и легко сообразить, что результирующий вектор  в точке
в точке 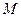 будет направлен горизонтально вдоль оси
будет направлен горизонтально вдоль оси 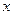 . Для нахождения модуля вектора
. Для нахождения модуля вектора  достаточно сложить проекции векторов
достаточно сложить проекции векторов 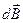 на ось
на ось 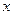 . Каждая такая проекция имеет вид
. Каждая такая проекция имеет вид
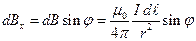 ,
,
где учтено, что угол 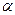 — между векторами
— между векторами 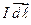 и
и 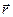 равен
равен 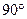 , поэтому синус равен единице. Проинтегрируем это выражение по всем
, поэтому синус равен единице. Проинтегрируем это выражение по всем 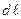
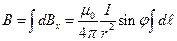 .
.
Интеграл 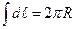 — есть длина окружности проводника с током, тогда
— есть длина окружности проводника с током, тогда
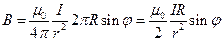 .
.
Учитывая, что 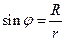 , запишем
, запишем
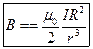
и, применяя теорему Пифагора, получим,
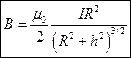 ,
,
а для напряженности магнитного поля
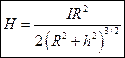 .
.
Магнитная индукция и напряженность магнитного поля в центре кругового тока, ( 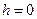 ,
, 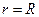 ) , соответственно равны
) , соответственно равны
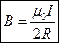 ,
, 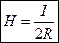 .
.
Взаимодействие параллельных проводников с током.
Единица силы тока.
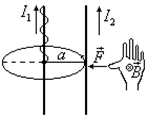
Найдем силу на единицу длины, с которой взаимодействуют в вакууме два параллельных бесконечно длинных провода с токами 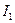 и
и 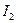 , если расстояние между проводами равно
, если расстояние между проводами равно 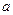 . Каждый элемент тока
. Каждый элемент тока 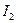 находится в магнитном поле тока
находится в магнитном поле тока 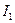 , а именно в поле
, а именно в поле 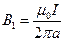 . Угол между каждым элементом тока
. Угол между каждым элементом тока 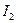 и вектором поля
и вектором поля 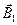 равен 90°.
равен 90°.
Тогда согласно закону Ампера, на участок 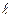 проводника с током
проводника с током 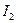 действует сила
действует сила
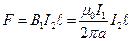 ,
,
а на единицу длины проводника эта сила будет равна
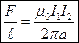 .
.
 |
Для силы действующей на единицу длины проводника с током 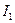 , получается, то же выражение. И наконец. Определяя направление вектора
, получается, то же выражение. И наконец. Определяя направление вектора 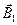 при помощи правила правого винта, и направление силы Ампера при помощи правила левой руки убедимся, что токи одинаково направленные, притягиваются, а противоположно направленные отталкиваются.
при помощи правила правого винта, и направление силы Ампера при помощи правила левой руки убедимся, что токи одинаково направленные, притягиваются, а противоположно направленные отталкиваются.
Если по проводникам, находящимся на расстоянии 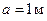 протекают одинаковые токи
протекают одинаковые токи 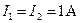 , то на каждый метр длины проводников действуют силы равные по
, то на каждый метр длины проводников действуют силы равные по 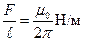 или, учитывая что
или, учитывая что 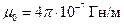 , получим
, получим
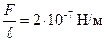 .
.
Из этого соотношения вводится единица измерения силы тока.
Ампер есть сила постоянного тока, который, будучи поддерживаемым, в двух параллельных, прямолинейных проводниках бесконечной длины и ничтожно малого кругового сечения, расположенных на расстоянии 1 м один от другого в вакууме, вызывает между этими проводниками возникновение силы взаимодействия на каждый метр длины равной 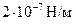 .
.
Графическое представление поля 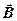 . Теорема Гаусса
. Теорема Гаусса
Как и другое векторное поле, поле  может быть представлено с помощью линий вектора
может быть представлено с помощью линий вектора  . Их проводят так, чтобы касательная к этим линиям в каждой точке совпадала с направлением вектора
. Их проводят так, чтобы касательная к этим линиям в каждой точке совпадала с направлением вектора  , а густота линий была бы пропорциональна модулю вектора
, а густота линий была бы пропорциональна модулю вектора  в данном месте. Полученная таким образом геометрическая картина позволяет судить о конфигурации данного магнитного поля. А теперь сформулируем теорему Гаусса для магнитного поля: Поток вектора
в данном месте. Полученная таким образом геометрическая картина позволяет судить о конфигурации данного магнитного поля. А теперь сформулируем теорему Гаусса для магнитного поля: Поток вектора  сквозь любую замкнутую поверхность равен нулю:
сквозь любую замкнутую поверхность равен нулю:
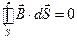 .
.
Она выражает тот факт, что линии вектора  не имеют ни начала, ни конца являются замкнутыми линиями. Поэтому число линий вектора
не имеют ни начала, ни конца являются замкнутыми линиями. Поэтому число линий вектора  , выходящих из любого объема, ограниченного замкнутой поверхностью
, выходящих из любого объема, ограниченного замкнутой поверхностью  , всегда равно числу линий, входящих в этот объем. Тогда и дивергенция векторного поля
, всегда равно числу линий, входящих в этот объем. Тогда и дивергенция векторного поля  всюду будет равной нулю
всюду будет равной нулю
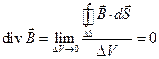 , или в другой записи
, или в другой записи 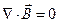 .
.
Это означает, что магнитное поле не имеет источников (магнитных зарядов). Магнитное поле порождают не магнитные заряды (которых в природе нет), а электрические токи. Этот закон является фундаментальным: он справедлив не только для постоянных, но и для переменных магнитных полей.
