Общие методические указания. ФИЗИКА Часть 3: Элементы квантовой физики и физики твердого тела, элементы физики атомного ядра и
И.А. Бабина
ФИЗИКА Часть 3: Элементы квантовой физики и физики твердого тела, элементы физики атомного ядра и
Элементарных частиц
Методические указания и контрольные задания для
студентов заочной формы обучения
| Челябинск |
Министерство образования и науки Российской Федерации
Южно-Уральский государственный университет
Кафедра техника и технологии в металлургии
53(07)
Б 125
И.А. Бабина
ФИЗИКА Часть 3: Элементы квантовой физики и физики твердого тела, элементы физики атомного ядра и
Элементарных частиц
Методические указания и контрольные задания для студентов заочной формы обучения
Челябинск
Издательский центр ЮУрГУ
УДК 53(076.5) +539.1(076.5) +530.145(076.5)
Б 125
Одобрено
учебно-методической комиссией совета филиала ЮУрГУ в г. Сатке
Рецензент Т.Н Новгородова, доцент к ф-м.н.
Бабина, И.А.
Б125 Физика Часть 3: Элементы квантовой физики и физики твердого тела, элементы физики атомного ядра и
элементарных частиц:методические указания и контрольные задания для студентов заочной формы обучения – Челябинск: Издательский центр ЮУрГУ, 2016. – 49с.
Цель настоящих методических указаний – оказать помощь студентам заочной формы обучения технических специальностей ЮУрГУ в изучении курса физики.
Методические указания и контрольные задания предназначены для студентов заочной формы обучения направлений: 08.03.01, 13.03.02, 18.03.01
УДК53(076.5) +539.1(076.5)+530.145(076.5)
| |
ОГЛАВЛЕНИЕ
Введение........................................................................ 4
1. Общие методические указания........................................ 5
2. Содержание курса «Физика».......................................................... 7
Раздел 5. Квантовая физика........................................................................ 7
Раздел 6. Квантовые статистики и физика твердого тела............. 8
Раздел 7. Элементы физики атомного ядра и элементарных
частиц................................................................................................................ 9
3. Основные формулы......................................................................... 10
4. Примеры решения задач............................................................... 16
Контрольная работа № 3.................................................................. 29
Приложения........................................................................................... 39
Библиографический список.............................................................. 47
| |
Введение
Физика – наука о наиболее простых и вместе с тем наиболее общих формах движения материи и их взаимных превращениях. Изучаемые физикой формы движения (механическая, тепловая и др.) присутствуют во всех высших и более сложных формах движения материи (химических, биологических и др.). Поэтому они, будучи наиболее простыми, являются в то же время наиболее общими формами движения материи.
Курс физики вместе с другими дисциплинами цикла общих математических и естественнонаучных дисциплин составляет основу теоретической подготовки инженеров и играет роль фундаментальной физико-математической базы, без которой не возможна успешная деятельность инженеров любого профиля.
Дисциплина «Физика» представляет собой целостный и фундаментальный курс, единый в своих частях и демонстрирующий роль физики как основы всего современного естествознания.
Изучение курса физики совместно с другими дисциплинами цикла способствует формированию у студентов современного естественнонаучного мировоззрения. Целостность курса физики является одной из фундаментальных предпосылок для воспитания образованного специалиста.
Цель настоящих методических указаний – оказать помощь студентам заочной формы обучения технических специальностей ЮУрГУ в изучении курса физики.
Общие методические указания
Дисциплина «Физика» изучается студентами всех технических специальностей заочной формы обучения Южно-уральского государственного университета в течение трех семестров.
Основной формой обучения студента заочной формы обучения является самостоятельная работа над учебным материалом. Эта работа организуется и направляется кафедрой общей физики ЮУрГУ. Преподаватели кафедры читают студентам установочные и обзорные лекции, проводят консультации, практические и лабораторные занятия, осуществляют текущий и итоговый контроль приобретенных знаний.
Процесс изучения физики студентами заочной формы обучения в каждом из учебных семестров состоит из следующих этапов:
1) проработка установочных и обзорных лекций;
2) самостоятельная работа над учебниками и учебными пособиями;
3) выполнение и защита контрольных работ;
4) прохождение лабораторного практикума;
5) сдача зачетов (если они предусмотрены учебным планом) и экзаменов.
Важнейшим аспектом самостоятельной работы студентов является выполнение контрольных работ. Контрольные работы позволяют закрепить теоретический материал курса. В процессе изучения физики студент должен выполнить три контрольные работы (по одной в семестр). Контрольные работы рецензируются преподавателем и, в случае необходимости, отправляются на доработку. Обязательным элементом является последующая защита контрольной работы студентом, которая может происходить как в течение семестра, так и во время сессии.
Основные разделы курса физики для инженерно-технических специальностей распределены по контрольным работам следующим образом.
Первая контрольная работа включает в себя физические основы механики, основы молекулярной физики и термодинамики.
Вторая – физические основы электродинамики и волновую оптику.
Третья – элементы квантовой физики, квантовые статистики и физики твердого тела, элементы физики атомного ядра и элементарных частиц.
Вариант задания контрольной работы для каждого студента определяет преподаватель.
Перед выполнением контрольной работы необходимо внимательно ознакомиться с примерами решения задач по данной контрольной работе, уравнениями и формулами, а также со справочными материалами, приведенными в методических указаниях.
Каждая контрольная работа оформляется в отдельной тетради. На титульном листе должны быть указаны: номер контрольной работы, наименование дисциплины, фамилия и инициалы студента, номер учебной группы, шифр и домашний адрес.
При решении задач по физике необходимо.
1. Внимательно прочитать условие задачи. Полностью переписать условие задачи в тетрадь. Сделать краткую запись, выразить все данные в СИ. Если позволяет характер задачи, необходимо сделать рисунок, поясняющий ее сущность.
2. Уточнить, какие величины требуется найти в результате решения задачи. Дать определения этих величин, записать для них соответствующие математические соотношения.
3. Установить круг физических явлений, относящихся к данной задаче, и физические законы, лежащие в их основе. Записать в общем виде математические выражения этих законов, а также соотношения между величинами, характеризующими установленные явления с количественной точки зрения.
4. Переписать все уравнения в соответствии с условиями задачи (ввести обозначения величин, учесть начальные и конечные условия, число состояний и количественный состав представленной в задаче физической системы).
5. Исходя из полученных соотношений, составить замкнутую систему уравнений (число уравнений совпадает с числом неизвестных). Решить ее любым известным математическим методом. (Следует помнить, что в ряде случаев «лишние» неизвестные могут сокращаться в процессе промежуточных математических преобразований).
6. Если конечное выражение для искомой величины является достаточно сложным, то его правильность желательно проверить методом размерности.
7. Необходимо помнить, что численные значения физических величин всегда являются приближенными. Поэтому при расчетах надо руководствоваться правилами действий с приближенными числами (прил. 4). Отметим, что для инженерных расчетов, как, впрочем, и для большинства физических, достаточна точность, обеспечиваемая тремя значащими цифрами.
8. Получив численный ответ, оценить его правдоподобность с позиций современной физики.
2. Содержание курса «Физика»
( III семестр изучения)
Раздел 5. КВАНТОВАЯ ФИЗИКА
Тема 13. Квантовая природа излучения
13.1. Тепловое излучение. Люминесценция. Абсолютно черное тело. Закон Кирхгофа.
13.2. Закон Стефана-Больцмана. Распределение энергии в спектре абсолютно черного тела. Закон смещения Вина.
13.3. Квантовая гипотеза и формула Планка.
13.4. Действие света. Фотоэффект и его виды. Внешний фотоэффект. Уравнение Эйнштейна для внешнего фотоэффекта. Фотоны.
13.5. Энергия, масса и импульс фотонов. Давление света. Квантовое и волновое его объяснение.
13.6. Эффект Комптона.
Тема 14. Элементы квантовой механики
14.1. Обоснование идей квантования (дискретности). Атомные спектры излучения и поглощения.
14.2. Постулаты Бора. Линейчатые спектры атомов (по Бору). Ионизация атомов и молекул.
14.3. Корпускулярно-волновой дуализм. Гипотеза де Бройля. Соотношения неопределенностей.
14.4. Задание состояния микрочастиц. Волновая функция. Вероятность в квантовой теории. Принцип суперпозиции.
14.5. Общее уравнение Шредингера. Стационарное уравнение Шредингера. Операторы физических величин. Принцип причинности в квантовой механике.
14.6. Свободная частица. Частица в потенциальной яме. Принцип соответствия Бора.
14.7. Прохождение частицы сквозь потенциальный барьер. Туннельный эффект.
14.8. Линейный гармонический осциллятор в квантовой механике.
Тема 15. Строение атома, молекулы
15.1. Водородоподобные атомы в квантовой механике. Квантовые числа: главное, орбитальное, магнитное. Энергетический спектр атомов и молекул.
15.2. Опыт Штерна и Герлаха. Спин электрона. Спиновое квантовое число.
15.3. Распределение электронов в атоме по состояниям. Принцип Паули. Периодическая система элементов.
15.4. Рентгеновские спектры. Молекулярные спектры.
15.5. Элементарная квантовая теория излучения. Спонтанное и вынужденное излучение. Лазер. Устройство и типы лазеров. Свойства лазерного излучения.
Раздел 6. Квантовые статистики и физика твердого тела
Тема 16. Элементы квантовой статистики
16.1. Фазовое пространство. Элементарная ячейка. Функция распределения. Квантовые идеальные газы. Вырождение газов. Принцип неразличимости тождественных частиц. Фермионы и бозоны.
16.2. Квантовые идеальные газы. Распределение Бозе. Фотонный и фононный газы. Распределение фотонов по энергиям.
16.3. Квантовые идеальные газы. Распределение Ферми. Распределение электронов проводимости в металле по энергиям при абсолютном нуле температур. Уровень Ферми.
Тема 17. Строение и свойства кристаллов. Кристаллическая решетка
17.1. Строение кристаллов. Экспериментальные методы исследования кристаллов. Кристаллическая решетка. Трансляционная симметрия. Элементарная ячейка. Точечные группы симметрии.
17.2. Точечные дефекты в кристаллах: вакансии, примеси внедрения и замещения.
17.3. Краевые и винтовые дислокации. Дислокации и пластичность.
Тема 18. Тепловые свойства твердых тел
18.1. Акустические и оптические колебания кристаллической решетки. Нормальные моды.
18.2. Нормальные осцилляторы. Понятие о фононах, о квазиимпульсе фонона.
18.3. Теплоемкость кристаллов при низких и высоких температурах.
Тема 19. Элементы зонной теории
19.1. Элементы зонной теории кристаллов. Волновые функции Блоха.
19.2. Зонная структура энергетического спектра электронов в моделях «сильной связи» и почти свободных электронов.
19.3. Заполнение зон: металлы, диэлектрики, полупроводники.
Тема 20. Электропроводность твердых тел
20.1. Электропроводность металлов. Носители тока в металлах. Недостаточность классической электронной теории. Явления сверхпроводимости.
20.2. Электропроводность полупроводников. Собственные полупроводники. Понятие дырочной проводимости.
20.3. Носители тока как квазичастицы. Эффективная масса электрона и дырки в кристалле.
20.4. Примесные полупроводники.
20.5. Фотоэлектрические явления в полупроводниках.
20.6. Контактные явления.
Тема 21. Магнитные свойства твердых тел
21.1. Магнитные свойства атомов. Магнетики.
21.2. Основные свойства диа- и парамагнетиков. Элементарная теория диа- и парамагнетизма.
21.3. Ферромагнетики. Их основные свойства. Магнитный гистерезис. Спиновая природа ферромагнетизма.
21.4. Антиферромагнетизм. Ферримагнетизм. Ферриты.
Раздел 7. ЭЛЕМЕНТЫ ФИЗИКИ АТОМНОГО ЯДРА И ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
Тема 22. Ядро и ядерные реакции
22.1. Состав ядра. Нуклоны. Магнитные и электрические свойства ядер.
22.2. Дефект масс и энергия связи ядра.
22.3. Взаимодействие нуклонов. Свойства и природа ядерных сил. Ядерные модели.
22.4. Радиоактивность. Закон радиоактивного превращения. Закономерности и происхождение альфа-, бета- и гамма- излучения атомных ядер. Взаимодействие излучения с веществом.
22.5. Ядерные реакции и их типы. Реакция деления ядра. Цепная реакция деления. Физические основы ядерной энергетики.
22.6. Реакции синтеза. Управляемые термоядерные реакции.
Тема 23. Элементарные частицы
23.1. Элементарные частицы и их классификация. Адроны. Кварки. Лептоны. Стандартная модель элементарных частиц.
23.2. Физический вакуум. Частицы и античастицы. Взаимопревращаемость элементарных частиц.
23.3. Типы фундаментальных взаимодействий. Характеристики фундаментальных взаимодействий. Симметрия законов природы. Кварки, лептоны и кванты фундаментальных полей.
23.4. Физическая картина мира. Вещество и поле. Корпускулярная и континуальная концепции описания природы. Незавершенность физики и будущее естествознания.
Основные формулы
Энергия теплового излучения, испускаемого черным телом за время t где 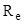 - энергетическая светимость черного тела, S – площадь его поверхности. - энергетическая светимость черного тела, S – площадь его поверхности. | 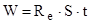 , , | |||||||
Закон Стефана – Больцмана где 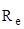 - энергетическая светимость черного тела; - энергетическая светимость черного тела; 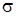 - постоянная Стефана - Больцмана; Т- термодинамическая температура. - постоянная Стефана - Больцмана; Т- термодинамическая температура. | 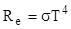 , , | |||||||
Закон смещения Вина где 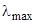 - длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости черного тела (максимальному значению функции Кирхгофа), b - постоянная Вина. - длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости черного тела (максимальному значению функции Кирхгофа), b - постоянная Вина. | 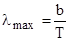 , , | |||||||
Формула Планка где 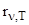 - спектральная плотность энергетической светимости черного тела, - спектральная плотность энергетической светимости черного тела, 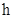 - постоянная Планка; с - скорость света в вакууме; - постоянная Планка; с - скорость света в вакууме; 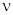 - частота излучения; Т - термодинамическая температура. - частота излучения; Т - термодинамическая температура. | 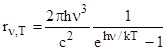 , , | |||||||
Давление, производимое светом при нормальном падении на поверхность непрозрачного тела где I - интенсивность падающего света (энергия всех фотонов, падающих на единицу поверхности в единицу времени), 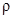 - коэффициент отражения, с - скорость света в вакууме. - коэффициент отражения, с - скорость света в вакууме. | 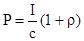 , , | |||||||
Энергия кванта (фотона) где 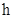 - постоянная Планка; с - скорость света в вакууме; - постоянная Планка; с - скорость света в вакууме; 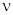 - частота излучения; - частота излучения; 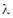 - длина волны. - длина волны. | 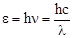 , , | |||||||
| Масса фотона |  , , | |||||||
| Импульс фотона | 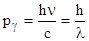 . . | |||||||
Уравнение Эйнштейна для внешнего фотоэффекта где 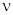 - частота падающего на катод света, - частота падающего на катод света, 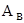 - работа выхода электрона из металла; m – масса электрона; - работа выхода электрона из металла; m – масса электрона; 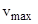 - максимальная скорость фотоэлектрона. - максимальная скорость фотоэлектрона. | 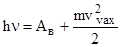 , , | |||||||
| Красная граница фотоэффекта | 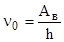 , , 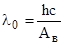 . . | |||||||
Обобщенная формула Бальмера где 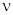 - частота излучения; - частота излучения; 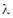 - длина волны, n=1,2,3, … - номер уровня, на который происходит переход; k = n+1, n+2, n+3…. - номер уровня, с которого происходит переход; R и - длина волны, n=1,2,3, … - номер уровня, на который происходит переход; k = n+1, n+2, n+3…. - номер уровня, с которого происходит переход; R и 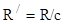 - постоянные Ридберга. - постоянные Ридберга. | 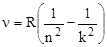 или или 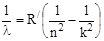 , , | |||||||
| Спектральные серии излучения атома водорода: | ||||||||
| серия Лаймана | n=1, k=2,3,4… | |||||||
| серия Бальмера | n=2, k=3,4,5… | |||||||
| серия Пашена | n=3, k=4,5,6,… | |||||||
| серия Брэкета | n=4, k=5,6,7,… | |||||||
| серия Пфунда | n=5, k=6,7,8,… | |||||||
| серия Хэмфри | n=6, k=7,8,9,… | |||||||
Радиус n-й стационарной орбиты электрона в атоме водорода в модели Бора где m – масса электрона, e –элементарный заряд, 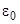 -электрическаяпостоянная, n=1, 2, … -электрическаяпостоянная, n=1, 2, … | 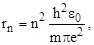 | |||||||
| Полная энергия электрона в атоме водорода n=1,2,3, … | 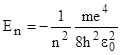 , , | |||||||
Длина волны де Бройля где 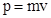 - импульс микрочастицы. - импульс микрочастицы. | 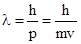 , , | |||||||
Соотношения неопределенностей Гейзенберга 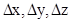 -неопределенности координат микрочастицы, -неопределенности координат микрочастицы, 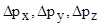 -неопределенности соответствующих проекций импульса, -неопределенности соответствующих проекций импульса, 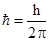 - постоянная Планка. - постоянная Планка. | 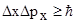 , , 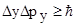 , , 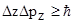 , , | |||||||
Вероятность нахождения микрочастицы dW в элементе объема dV вблизи точки с координатами (x,y,z) где 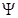 - волновая функция, зависящая от координат и времени (x, y, z, t). - волновая функция, зависящая от координат и времени (x, y, z, t). | 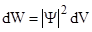 , , | |||||||
| Вероятность обнаружить частицу в момент времени t в конечном объеме V | 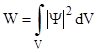 | |||||||
| Плотность вероятности нахождения частицы в соответствующем месте пространства | 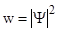 | |||||||
| Общее уравнение Шредингера(уравнение Шредингера, зависящее от времени) | ||||||||
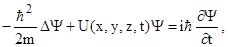 | ||||||||
где m - масса частицы, 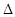 - оператор Лапласа, i - мнимая единица, U(x,y,z,t) - потенциальная функция частицы в силовом поле, в котором она движется, - оператор Лапласа, i - мнимая единица, U(x,y,z,t) - потенциальная функция частицы в силовом поле, в котором она движется, 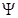 (x,y,z,t) - искомая волновая функция частицы. (x,y,z,t) - искомая волновая функция частицы. | ||||||||
| Уравнение Шредингера для стационарных состояний | ||||||||
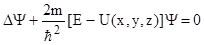 , , | ||||||||
где Е – полная энергия, U=U(x,y,z,) - потенциальная энергия частицы,  - оператор Лапласа. - оператор Лапласа. | ||||||||
Полная энергия частицы, находящейся в одномерной потенциальной яме с бесконечно высокими стенками где n=1,2,3,… - главное квантовое число, m - масса частицы, 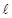 -ширинапотенциальной ямы -ширинапотенциальной ямы | 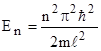 , , | |||||||
| Собственные волновые функции такой частицы где n=1,2,3,…. | 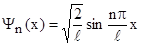 , , | |||||||
| Стационарное уравнение Шредингера для электрона в водородоподобном атоме | ||||||||
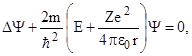 | ||||||||
| где m – масса электрона, Е – полная энергия электрона в атоме. | ||||||||
| Собственные значения энергии электрона в водородоподобном атоме где n=1, 2, 3, … - главное квантовое число. | 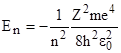 , , | |||||||
Момент импульса(механический орбитальный момент импульса) электрона где 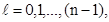 – орбитальное квантовое число. – орбитальное квантовое число. | 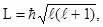 | |||||||
Проекция момента импульса электрона на направление Z внешнего магнитного поля где 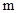 - магнитное квантовое число,которое, при заданном - магнитное квантовое число,которое, при заданном 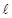 , может принимать значения: , может принимать значения: 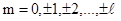 | 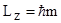 | |||||||
| Спин электрона - собственный (неуничтожимый) механический момент импульса где s=1/2 - спиновое квантовое число. | 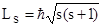 , , | |||||||
Проекция спина электрона на направление внешнего магнитного поля где 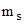 = = 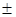 1/2 - магнитное спиновое квантовое число. 1/2 - магнитное спиновое квантовое число. | 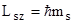 , , | |||||||
| Молярная теплоемкость кристаллической решетки | ||||||||
при температуре 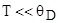 : : | 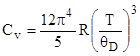 , , | |||||||
при температуре 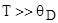 : : | 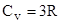 , , | |||||||
где R – молярная газовая постоянная, Т – температура кристалла, 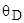 - характеристическая температура Дебая. - характеристическая температура Дебая. | ||||||||
| Символическая запись ядра где Х - символ химического элемента, Z - зарядовое число (число протонов в ядре, совпадающее с порядковым номером в периодической таблице элементов), А - массовое число (число нуклонов в ядре). | 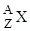 , , | |||||||
Дефект массы ядра где 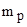 , , 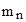 , , 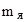 - соответственно массы протона, нейтрона и ядра, - соответственно массы протона, нейтрона и ядра, 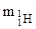 - масса атома водорода, m - масса атома водорода, m 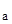 - масса атома. - масса атома. | 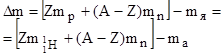 | |||||||
| Энергия связи нуклонов в ядре | 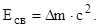 | |||||||
Закон радиоактивного распада где N - число нераспавшихся ядер в момент времени t; 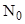 - число нераспавшихся ядер в начальный момент (при t=0); е - основание натурального логарифма; - число нераспавшихся ядер в начальный момент (при t=0); е - основание натурального логарифма; 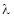 - постоянная радиоактивного распада. - постоянная радиоактивного распада. | 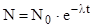 , , | |||||||
| Период полураспада | 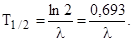 | |||||||
| Среднее время жизни радиоактивного ядра | 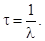 | |||||||
Активность нуклида (активность изотопа) где 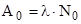 - активность изотопа в начальный момент времени (t=0). - активность изотопа в начальный момент времени (t=0). | 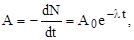 | |||||||
| Правила смещения: | ||||||||
для 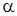 - распада - распада | 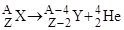 , , | |||||||
для 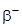 - распада - распада | 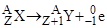 , , | |||||||
для 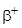 - распада - распада | 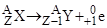 . . | |||||||
Символическая запись ядерной реакции где 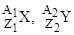 - исходное и конечное ядра, соответственно с зарядовыми числами - исходное и конечное ядра, соответственно с зарядовыми числами 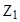 и и 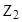 и массовыми числами и массовыми числами 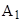 и и 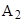 ; а и b - соответственно бомбардирующая и испускаемая (или испускаемые) в ядерной реакции частицы. ; а и b - соответственно бомбардирующая и испускаемая (или испускаемые) в ядерной реакции частицы. | 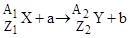 или или 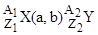 , , | |||||||
Энергия ядерной реакции (ее энергетический эффект) где 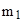 и и 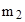 - массы покоя ядра мишени и бомбардирующей частицы; - массы покоя ядра мишени и бомбардирующей частицы; 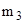 и и 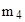 - массы покоя ядер (частиц) продуктов реакции. - массы покоя ядер (частиц) продуктов реакции. | 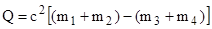 , , | |||||||
Примеры решения задач
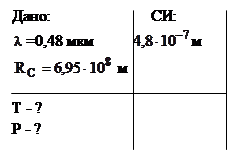 Пример 1. Максимум спектральной плотности энергетической светимости Солнца приходится на длину волны
Пример 1. Максимум спектральной плотности энергетической светимости Солнца приходится на длину волны 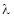 =0,48 мкм. Считая, что Солнце излучает как черное тело, определить: 1) температуру его поверхности; 2) мощность, излучаемую его поверхностью.
=0,48 мкм. Считая, что Солнце излучает как черное тело, определить: 1) температуру его поверхности; 2) мощность, излучаемую его поверхностью.
Решение
Согласно закону смещения Вина, искомая температура поверхности Солнца:
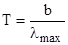 , (1)
, (1)
где b= 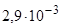
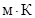 - постоянная Вина.
- постоянная Вина.
Мощность, излучаемая поверхностью Солнца:
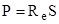 , (2)
, (2)
где 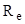 - энергетическая светимость черного тела (Солнца),
- энергетическая светимость черного тела (Солнца), 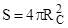 - площадь поверхности Солнца,
- площадь поверхности Солнца, 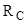 - радиус Солнца.
- радиус Солнца.
Согласно закону Стефана - Больцмана:
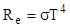 , (3)
, (3)
где 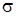 =
= 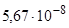 Вт/
Вт/ 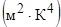 - постоянная Стефана - Больцмана.
- постоянная Стефана - Больцмана.
Подставим записанные выражения в формулу (2), найдем искомую мощность, излучаемую поверхностью Солнца:
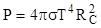 . (4)
. (4)
Вычисляя, получим: Т=6,04 кК; Р= 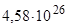 Вт.
Вт.
Пример 2.Определить длину волны 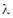 , массу и импульс фотона с энергией
, массу и импульс фотона с энергией 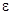 = 1 МэВ.
= 1 МэВ.
 Решение
Решение
Энергия фотона связана с дли- ной волны света соотношением: 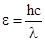 ,
,
где h – постоянная Планка, с – скорость света в вакууме. Отсюда 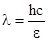 .
.
Подставив численные значения, получим: 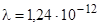 м.
м.
Массу фотона определим, используя формулу Эйнштейна 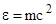 . Масса фотона
. Масса фотона 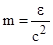 =
= 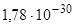 кг.
кг.
Импульс фотона 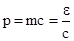 =
= 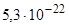 кг м/с.
кг м/с.
Пример 3. Натриевый катод вакуумного фотоэлемента освещается монохроматическим светом с длиной волны 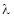 =40 нм. Определить задерживающее напряжение, при котором фототок прекращается. "Красная граница" фотоэффекта для натрия
=40 нм. Определить задерживающее напряжение, при котором фототок прекращается. "Красная граница" фотоэффекта для натрия 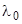 =584 нм.
=584 нм.
 Решение
Решение
Электрическое поле, препят- ствующее движению электронов от катода к аноду, называют обратным. Напряжение, при котором фототок полностью прекращается, называется задерживающим напряжением. При таком задерживающем напряжении 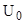 ни один из электронов, даже обладающий при вылете из катода максимальной скоростью
ни один из электронов, даже обладающий при вылете из катода максимальной скоростью 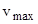 , не может преодолеть задерживающего поля и достигнуть анода. При этом начальная кинетическая энергия фотоэлектронов (
, не может преодолеть задерживающего поля и достигнуть анода. При этом начальная кинетическая энергия фотоэлектронов ( 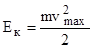 ) переходит в потенциальную (
) переходит в потенциальную ( 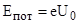 , где е=
, где е= 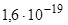 Кл – элементарный заряд, а
Кл – элементарный заряд, а 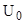 - наименьшее задерживающее напряжение). По закону сохранения энергии
- наименьшее задерживающее напряжение). По закону сохранения энергии
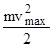 =
= 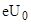 . (1)
. (1)
Кинетическую энергию электронов найдем, используя уравнение Эйнштейна для внешнего фотоэффекта:
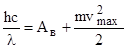 . (2)
. (2)
Отсюда 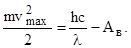 (3)
(3)
Работа выхода электронов Ав определяется красной границей фотоэффекта:
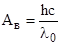 . (4)
. (4)
Подставив выражение (4) в уравнение (3), получим:
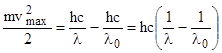 .
.
Тогда, из уравнения (1) 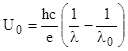 .
.
Вычисляя, получим 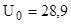 В.
В.
 Пример 4.Кинетическая энергия протона в четыре раза меньше его энергии покоя. Вычислить длину волны де Бройля для протона.
Пример 4.Кинетическая энергия протона в четыре раза меньше его энергии покоя. Вычислить длину волны де Бройля для протона.
Решение
Длина волны де Бройля определяется по формуле: 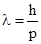 , (1)
, (1)
где h – постоянная Планка, 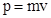 - импульс частицы.
- импульс частицы.
По условию задачи кинетическая энергия протона сравнима по величине с его энергией покоя Е0. Следовательно, импульс и кинетическая энергия связаны между собой релятивистским соотношением:
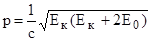 , (2)
, (2)
где с – скорость света в вакууме.
Используя условие задачи, получим: 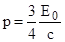 . Подставив полученное выражение в формулу (1), найдем длину волны де Бройля:
. Подставив полученное выражение в формулу (1), найдем длину волны де Бройля:
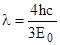 .
.
Энергию покоя электрона найдем по формуле Эйнштейна 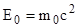 , где m0 - масса покоя электрона, с - скорость света в вакууме.
, где m0 - масса покоя электрона, с - скорость света в вакууме.
Подставив числовые значения, получим: 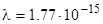 м.
м.
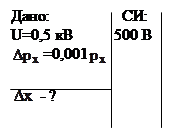 Пример 5. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U=0,5 кВ. Принимая, что неопределенность импульса электрона равна 0,1 % от его числового значения, определить неопределенность координаты электрона. Является ли в данных условиях электрон квантовой или классической частицей?
Пример 5. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U=0,5 кВ. Принимая, что неопределенность импульса электрона равна 0,1 % от его числового значения, определить неопределенность координаты электрона. Является ли в данных условиях электрон квантовой или классической частицей?
Решение
В направлении движения пучка электронов (ось X) соотношение неопределенностей имеет вид:
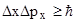 , (1)
, (1)
где 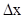 - неопределенность координаты электрона;
- неопределенность координаты электрона; 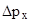 - неопределенность его импульса;
- неопределенность его импульса; 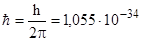
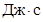 - постоянная Планка.
- постоянная Планка.
Пройдя ускоряющую разность потенциалов, электрон приобретает кинетическую энергию 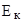 , равную работе сил электрического поля:
, равную работе сил электрического поля:
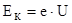 .
.
Расчет дает значение Ек=500 эВ, что много меньше энергии покоя электрона (Е0 = 0,51 Мэв). Следовательно, в данных условиях электрон является нерелятивистской частицей, имеющей импульс, связанный с кинетической энергией формулой 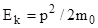 .
.
Тогда: 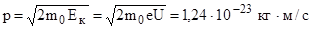 .
.
Согласно условию задачи, неопределенность импульса 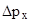 =0,001
=0,001 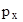 =
= 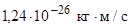 , т.е.
, т.е. 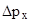 <<
<< 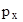 .
.
Это значит, что волновые свойства в данных условиях несущественны и электрон может рассматриваться как классическая частица. Из выражения (1) следует, что искомая неопределенность координаты электрона
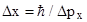 .
.
Вычислив, получим 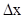
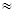 8,51 нм.
8,51 нм.
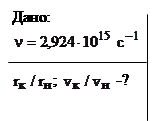 Пример 6. В результате перехода из одного стационарного состояния в другое атомом водорода был испущен квант с частотой
Пример 6. В результате перехода из одного стационарного состояния в другое атомом водорода был испущен квант с частотой 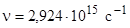 . Найти, как изменились радиус орбиты и скорость движения электрона, используя теорию Бора.
. Найти, как изменились радиус орбиты и скорость движения электрона, используя теорию Бора.
Решение
Излучение с частотой 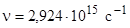 соответствует длине волны
соответствует длине волны 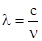 = =102,6 нм (с – скорость света в вакууме), лежащей в ультрафиолетовой области. Следовательно, спектральная линия принадлежит серии Лаймана, возникающей при переходе электрона на первый энергетический уровень (n=1).
= =102,6 нм (с – скорость света в вакууме), лежащей в ультрафиолетовой области. Следовательно, спектральная линия принадлежит серии Лаймана, возникающей при переходе электрона на первый энергетический уровень (n=1).
Используем обобщенную формулу Бальмера, чтобы определить номер энергетического уровня (k), с которого был совершен переход: 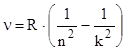 .
.
Выразим из этой формулы k:
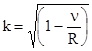 .
.
Подставляя имеющиеся данные, получим k=3. Следовательно, излучение произошло в результате перехода электрона с третьей орбиты на первую.
Значения радиусов 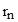 орбит и скоростей движения электронов
орбит и скоростей движения электронов 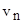 на этих орбитах найдем из следующих соображений.
на этих орбитах найдем из следующих соображений.
На электрон, находящийся на стационарной орбите в атоме водорода, со стороны ядра действует сила Кулона
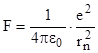 ,
,
которая сообщает ему нормальное ускорение 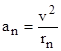 . Следовательно, согласно основному закону динамики:
. Следовательно, согласно основному закону динамики:
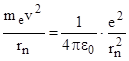 . (1)
. (1)
Кроме того, согласно постулату Бора, момент импульса электрона на стационарной орбите должен быть кратен постоянной Планка, т.е.
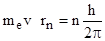 , (2)
, (2)
где n = 1, 2, 3 …. – номер стационарной орбиты.
Из уравнения (2) скорость 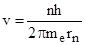 . Подставив это выражение в уравнение (1), получим
. Подставив это выражение в уравнение (1), получим
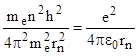 .
.
Отсюда радиус стационарной орбиты электрона в атоме водорода: 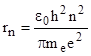 .
.
Тогда скорость электрона на этой орбите:
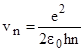 .
.
Принимая, что до излучения кванта электрон имел характеристики r3, v3, а после излучения r1, v1 несложно получить:
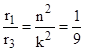 ;
; 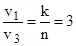 ,
,
то есть, радиус орбиты уменьшился в 9 раз, скорость электрона увеличилась в 3 раза.
Пример 7. Электрон в одномерной прямоугольной "потенциальной яме" шириной 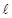 =200 пм с бесконечно высокими "стенками" находится в возбужденном состоянии (n=2). Определить: 1) вероятность W обнаружения электрона в средней трети "ямы"; 2) точки указанного интервала, в которых плотность вероятности обнаружения электрона максимальна и минимальна.
=200 пм с бесконечно высокими "стенками" находится в возбужденном состоянии (n=2). Определить: 1) вероятность W обнаружения электрона в средней трети "ямы"; 2) точки указанного интервала, в которых плотность вероятности обнаружения электрона максимальна и минимальна.
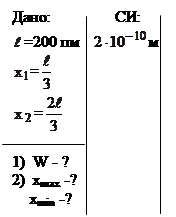
Решение
1. Вероятность обнаружить частицу в интервале 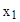 <x<
<x< 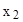 равна:
равна:
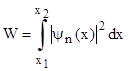 . (1)
. (1)
Возбужденному состоянию (n=2) отвечает собственная волновая функция:
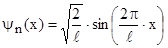 . (2)
. (2)
Подставим (2) в (1) и учтем, что 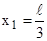 и
и 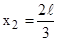 :
:
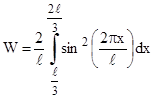 .
.
Выразив 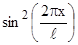 через косинус двойного угла с использованием тригонометрического равенства
через косинус двойного угла с использованием тригонометрического равенства 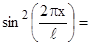
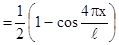 , получим выражение для искомой вероятности:
, получим выражение для искомой вероятности: 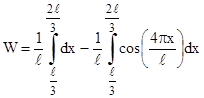 = =
= = 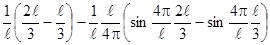 = =
= = 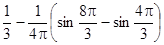 = 0,195.
= 0,195.
2. Плотность вероятности существования частицы в некоторой области пространства определяется квадратом модуля ее волновой функции 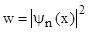 . Используя выражение (2), получим:
. Используя выражение (2), получим:
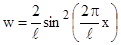 . (3)
. (3)
Зависимость квадрата модуля волновой функции частицы от ее координаты, определяемая выражением (3), приведена на рисунке.
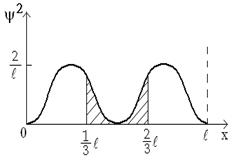 Очевидно, что минимальная плотность вероятности w=0 соответствует значениям x, при которых
Очевидно, что минимальная плотность вероятности w=0 соответствует значениям x, при которых 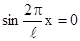 .
.
То есть, 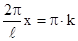 ,
,
где k = 0, 1, 2…
Отсюда 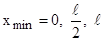 .
.
Максимального значения в пределах ямы плотность вероятности w достигает при условии: 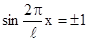 . Соответствующие значения
. Соответствующие значения 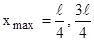 .
.
Как видно из графика зависимости w= w(x), приведенного на рисунке, в интервал 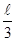 <x<
<x< 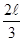 попадает только значение
попадает только значение 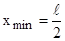 . В пределах указанного интервала плотность вероятности w достигает максимального значения на границах интервала при
. В пределах указанного интервала плотность вероятности w достигает максимального значения на границах интервала при 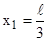 или
или 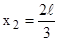 . Найдем значения w на границах указанного интервала, используя выражение (3):
. Найдем значения w на границах указанного интервала, используя выражение (3):
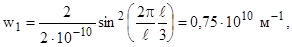
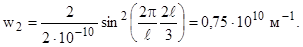
Как видим, плотность вероятности обнаружить электрон на границах заданного интервала - одинакова. Следовательно, 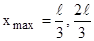 ,
, 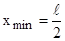 .
.
Пример 8.Определить количество теплоты, необходимое для нагревания кристалла NaCl массой m=20г на 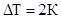 от температуры Т1 = 2К. Характеристическую температуру Дебая
от температуры Т1 = 2К. Характеристическую температуру Дебая 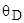 для NaCl принять равной 320К..
для NaCl принять равной 320К..
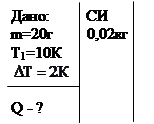
Решение
Количество теплоты, необходимое для нагревания тела массой m от температуры Т1 до температуры Т2 можно вычислить по формуле:
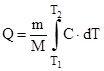 , (1)
, (1)
где С – молярная теплоемкость вещества, М – молярная масса.
Согласно теории Дебая, при температуре 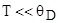 молярная теплоемкость кристаллических твердых тел определяется выражением:
молярная теплоемкость кристаллических твердых тел определяется выражением:
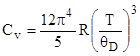 . (2)
. (2)
Подставив выражение (2) в (1), и проинтегрировав, получим:
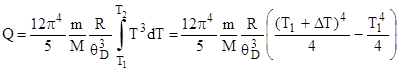 .
.
Подставив численные значения и произведя вычисления, найдем Q= 1,22 мДж.
Пример 9. Вычислить дефект массы, энергию связи и удельную энергию связи ядра 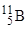 .
.
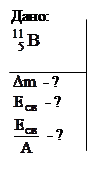 Решение
Решение
Дефект массы ядра определим по формуле:
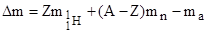 . (1)
. (1)
Для ядра 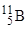 : Z=5; А=11.
: Z=5; А=11.
Вычисление дефекта массы выполним во внесистемных единицах – атомных единицах массы (а.е.м.). Необходимые данные возьмем из таблицы (приложение 3):
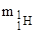 =1,00783 а.е.м.,
=1,00783 а.е.м., 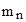 =1,00867 а.е.м.,
=1,00867 а.е.м., 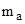 = 11,00931 а.е.м.
= 11,00931 а.е.м.
В результате расчета по формуле (1) получим:  =0,08186 а.е.м.
=0,08186 а.е.м.
Энергию связи ядра найдем также во внесистемных единицах (МэВ), воспользовавшись формулой:
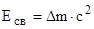 . (2)
. (2)
Коэффициент пропорциональности 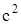 = 931,4 МэВ/а.е.м., т.е.
= 931,4 МэВ/а.е.м., т.е.
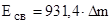 .
.
После подстановки численных значений получим:
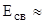 76,24 МэВ.
76,24 МэВ.
Удельная энергия связи, по определению, равна:
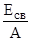
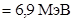 .
.
Примечание.Расчет дефекта массы ядра должен проводиться с максимально возможной точностью, т.е. с учетом всех значащих цифр, указанных в табличных данных.
Пример 10. Определить период полураспада радиоактивного изотопа, если известно, что за 1 сутки из 1 млн ядер распадается 175 тысяч.
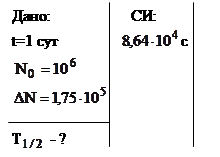 Решение
Решение
Период полураспада связан с постоянной радиоактивного распада соот- ношением:
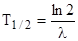 . (1)
. (1)
Постоянную радиоактивного распада 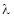 найдем, используя закон радиоактивного распада:
найдем, используя закон радиоактивного распада:
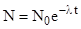 , (2)
, (2)
где N – число ядер, не распавшихся к моменту времени t, 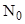 - начальное число ядер.
- начальное число ядер.
Разделив уравнение (2) на 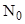 и прологарифмировав обе части, получим:
и прологарифмировав обе части, получим:
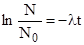 или
или 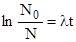 .
.
Отсюда: 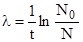 .
.
Учет того, что N= 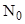 -
- 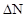 , дает:
, дает:
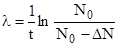 .
.
Подставив это выражение в (1), получим для периода полураспада следующее выражение:
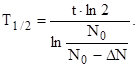
Подстановка численных значений и расчет приводят к результату 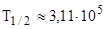 с.
с.
Примечание. Решая задачи подобного типа, допускается использование внесистемных единиц измерения времени, таких как - час, сутки, год.
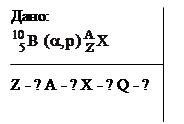 Пример 11. При соударении
Пример 11. При соударении 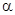 - частицы с ядром бора
- частицы с ядром бора 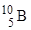 произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер оказалось ядро атома водорода
произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер оказалось ядро атома водорода 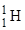 . Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить ее энергетический эффект.
. Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить ее энергетический эффект.
Решение
Обозначим неизвестное ядро символом 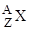 .
.
Так как 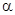 - частица представляет собой ядро гелия
- частица представляет собой ядро гелия 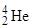 , запись
, запись
реакции будет иметь вид:
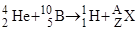 .
.
Применив закон сохранения массового числа, получим:
4+10=1+А,
отсюда А=13.
Применив закон сохранения зарядового числа, получим:
2+5=1+Z,
отсюда Z=6.
По периодической системе элементов найдем, что неизвестное ядро является ядром изотопа углерода 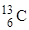 .
.
В окончательном виде реакцию можно записать так:
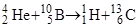 .
.
Определим энергию реакции (энергетический эффект) по формуле:
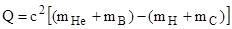 . (1)
. (1)
Заменив массы ядер массами нейтральных атомов, получим
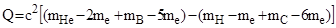 ,(2)
,(2)
где 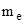 - масса электрона.
- масса электрона.
Упростив уравнение (2), получим:
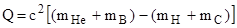 . (3)
. (3)
Массы атомов найдем в таблице приложения 3 :
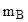 =10,01294 а.е.м.,
=10,01294 а.е.м., 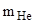 =4,00260 а.е.м.,
=4,00260 а.е.м.,
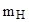 =1,00783 а.е.м.,
=1,00783 а.е.м., 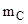 =13,00335 а.е.м.
=13,00335 а.е.м.
Подставив в (3) массы атомов в а.е.м., а с учетом того, что коэффициент пропорциональности 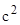 =931,4 МэВ/а.е.м., получим:
=931,4 МэВ/а.е.м., получим:
Q=4,06 МэВ.
Реакция идет с выделением тепла, т.е. является экзотермической.
Контрольная работа № 3
Таблица выбора вариантов индивидуального задания
| Вариант | Номера задач | ||||||||||
1. Найти, какое количество энергии излучает за 1 с один квадратный сантиметр поверхности абсолютно черного тела, если известно, что максимальная спектральная плотность его энергетической светимости приходится на длину волны 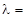 484 нм.
484 нм.
2. Как меняется температура черного тела, если при ее изменении максимум спектральной плотности энергетической светимости смещается с красной границы видимого спектра 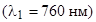 на фиолетовую
на фиолетовую 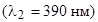 .
.
3. Температура черного тела увеличилась в два раза, в результате чего длина волны, соответствующая максимальной спектральной плотности энергетической светимости уменьшилась на 600 нм. Определить начальную и конечную температуры тела.
4. При нагревании черного тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась от 0,69 до 0,5 мкм. Во сколько раз увеличилась при этом энергетическая светимость тела?
