Построение контролирующего теста для дискретного комбинационного объекта. Построение тестов методом таблиц функций неисправности
Построение тестов методом таблиц функций неисправности
1. Запишем логическое выражение работы схемы
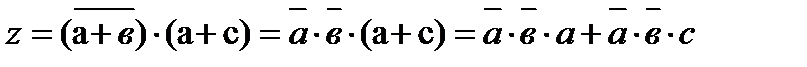, для случаев неисправности в узлах 4,5 запишем выражение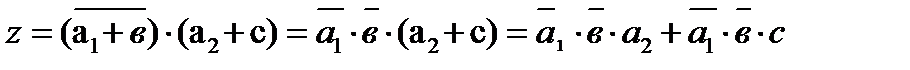 
На основании полученных выражений строим таблицу неисправности
| № узла | Вид неиспр. | Переменная в узле | Ф-ции неиспр | |
| а=0 | 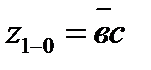 | е1 | ||
| а=1 | 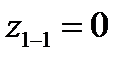 | е2 | ||
| в=0 | 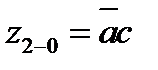 | е3 | ||
| в=1 | 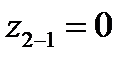 | е4 | ||
| с=0 | 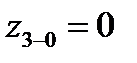 | е5 | ||
| с=1 | 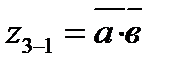 | е6 | ||
| а1=0, а2=а | 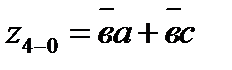 | е7 | ||
| а1=1, а2=а | 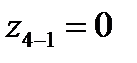 | е8 | ||
| а1=а, а2=0 | 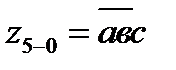 | е9 | ||
| а1=а, а2=1 | 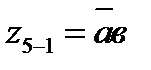 | е10 | ||
| y1=0 | 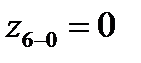 | е11 | ||
| y1=1 | 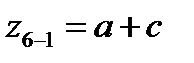 | е12 | ||
| y2=0 | 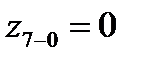 | е13 | ||
| y2=1 | 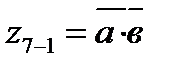 | е14 | ||
| z=0 | 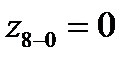 | е15 | ||
| z=1 | 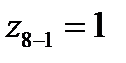 | е16 |
На основании данной таблицы составим таблицу функций неисправности. В этой таблице записываются выходные сигналы для всех неисправностей плюс исправные схемы при всех возможных наборах входных сигналов.
Таблица функций неисправности включает в себя все возможные наборы входных сигналов и значения выходных сигналов для всех возможных неисправностей и исправной схемы.
| № | а | в | с | е0 | е1 | е2 | е3 | е4 | е5 | е6 | е7 | е8 | е9 | е10 | е11 | е12 | е13 | е14 | е15 | е16 |
а,в,с – входные сигналы, е0 – выходные сигналы исправной системы, е11-е16 –выходные сигналы при соответствующих неисправностях.
При анализе таблицы функции неисправности можно выделить неразличимые и не обнаруживаемые неисправности, в частности не обнаруживающей является неисправность е9 поскольку при всех наборах входных переменных значение выхода схемы соответствует выходу исправной схемы.
Построение контролирующего теста для дискретного комбинационного объекта.
Дискретным комбинационным н-ся устройство, выходные сигналы которого являются функцией только входных сигналов в данный момент времени.
Контролирующий тест представляет собой несколько наборов входных переменных: а, в, с. Он должен быть минимальным. Контролирующий тест позволяет выявить только наличие неисправностей. Место неисправности в большинстве случаев выявить невозможно.
Для построения минимального контролирующего теста вначале составляем таблицу покрытия для функции е0-еj, входные наборы должны быть обозначены, а в клетках таблицы будет результат сравнения выходных сигналов исправной схемы и рассмотрим неисправности.
| № набора | Результат сравнения | a | b | c | |||||||
| e0-e1 | e0-e2 | e0-e3 | e0-e6 | e0-e7 | e0-e12 | e0-e16 | |||||
| А | |||||||||||
| В | |||||||||||
| С | |||||||||||
| D | |||||||||||
| E | |||||||||||
| F | |||||||||||
| G | |||||||||||
| H |
На основании таблицы покрытия записывается формула покрытия по следующему правилу, для каждого столбца записывается логическая сумма наборов, дающих 1, а затем берется логическое произведение для всех столбцов.
Фп=F*B*D*A*(E+F)*(D+E+F+G+H)*(A+C+D+E+F+G+H)=[закон поглощения]=F*B*D*A
| № набора | Вх.си | e0 | Неисправности | |||||||||
| a | b | c | e1 | e2 | e3 | e6 | e7 | e12 | e16 | |||
| F | ||||||||||||
| В | ||||||||||||
| D | ||||||||||||
| A |
Фп=F*B*D*A
Если в формуле покрытия получилась логическая сумма нескольких произведений, то выбирается из слагаемых, которые имеют меньшее количество сомножителей.
Неисправность выявляется следующим образом, на входы схемы последовательно подаются наборы 6-2-4-1 и смотрим сигнал на выходе.