Розділ 2. Принципи спеціальної теорії відносності. 1 страница
Дослідних даних.
§1. Предмет класичної електродинаміки. Експериментальні основи електродинаміки.
Існує велике коло фізичних явищ, зв'язаних із взаємодією між собою електрично заряджених тел. По існуючим уявленням ця взаємодія здійснюється за допомогою електромагнітного поля. Теорія поведінки електромагнітного поля, що здійснює взаємодію між електричними зарядами, називається електродинамікою. В даний час, у силу наявності у електромагнітного поля квантових властивостей, розрізняють дві електродинамічні теорії – класичну і квантову електродинаміку. Тут ми будемо займатися винятково класичною електродинамікою (ЕД), а про квантову електродинаміку (КЕД) див. у частині V цього курсу.
Предмет класичної електродинаміки уточнимо в такий спосіб. ЕД – це неквантова теорія поведінки електромагнітного поля, що здійснює взаємодію між електричними зарядами. Як відомо (див. вступ §1, ч.I), для подальшого уточнення предмета фізичної теорії необхідно вказати ті абстрактні ідеалізовані об'єкти, які теорія описує точно (а не приблизно). Таким основним ідеалізованим об'єктом ЕД є так називане класичне (неквантове) електромагнітне поле (тому що в частині II ми будемо вивчати тільки класичні поля, тому термін "класичне" ми будемо, як правило, для стислості опускати, сподіваючись, що це не викликає непорозумінь). Тому можна також сказати, що предметом ЕД є поведінка класичного електромагнітного поля, що здійснює взаємодію між електричними зарядами. Хоча повне, точне уявлення про ідеалізований об'єкт можна одержати тільки після побудови теорії. Приведемо вже тут найважливіші якісні відомості про класичні поля.
Електромагнітне поле є одним з видом фізичних полів. Класичне фізичне поле – це особлива (відмінна від речовини) форма фізичної реальності, що характеризується наступними відмінними (істотними) загальними властивостями:
1) це є фізична система з нескінченним числом ступенів свободи (тому що має властивість безперервності (континуальності));
2) фізичне поле для свого руху (поширення) не вимагає речовинного носія (наприклад, у вигляді ефіру): цим фізичне поле істотне відрізняється від математичних полів, часто використовуваних у фізиці (таких як поле температур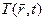 
у газі, поля швидкостей часток рідини 
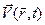, тензорне поле напруг суцільного середовища і т.д.), що є характеристиками речовини і, отже, без наявності речовини існувати не можуть;
3) фізичне поле обумовлюється (створюється, породжується) фізичними зарядами;
4) воно здійснює силову дію на ті фізичні заряди, якими саме може обумовлюватися.
Зауваження. З викладеного видно, що на зміну уявлень МКС про абсолютну дискретність фізичної реальності прийшли нові протилежні представлення ЕМКС про її абсолютну безперервність. З погляду матеріалістичної діалектики як ті, так і інші представлення носять метафізичний, тобто не діалектичний характер, зв'язаний з абсолютизацією однієї з категорій діалектично "сполученої" пари категорій "дискретність – безперервність". Іншими словами, метафизичність таких уявлень про матерію зв'язна з неврахуванням (знехтуванням) відомого діалектичного взаємозв'язку між парними (протилежними) категоріями матеріалістичної діалектики, що суперечить основному її закону єдності і боротьби протилежностей. Отже, з позицій філософської діалектики необхідний деякий синтез представлень МКС і ЕДКС про фізичну форму руху матерії, діалектично "щознімає" ці моменти абсолютності, і що виявляє відносний характер дискретних і безперервних властивостей фізичної реальності. Саме такий синтез і був здійснений у рамках КПКС, перші уявлення якої виникли тільки ХХ сторіччі.
Викладені вище загальні властивості фізичних полів дозволяють дати якісне уявлення про класичне електромагнітне поле. Електромагнітне поле – це один із видів фізичних полів, що:
1) обумовлюється (створюється) електричними зарядами; 2) здійснює силову дію на електричні заряди. Електричне поле – це така сторона (окремий випадок) електромагнітного поля, що: 1) може обумовлюватися навіть нерухомими зарядами; 2) здійснює силовий вплив навіть на нерухомі електричні заряди. Магнітне поле – така сторона електромагнітного поля, що: 1) обумовлюється тільки електричними зарядами що рухаються (а не покояться), тобто електричними струмами; 2) здійснює силову дію тільки на електричні заряди, що рухаються, тобто на електричні струми.
Зауваження. Як ми переконаємося нижче, вихрові електричні і магнітні поля можуть обумовлюватися також і змінними в часі магнітними й електричними полями, відповідно. Ці явища є основою механізму руху (поширення) електромагнітних полів, що не вимагає для себе ніякого речовинного носія.
Для теоретичного опису електромагнітних полів, тобто для одержання теоретичних законів електродинаміки необхідно теоретично узагальнити наявні емпіричні факти і закони з області електромагнітних явищ. В основу таких узагальнень можна покласти різні "набори" таких дослідних даних, тобто їхній вибір при побудові теорії неоднозначний. При цьому можна орієнтуватися або на історичний шлях розвитку електродинаміки, або на розуміння зручності і простоти викладу матеріалу. При правильному узагальненні ми повинні одержати єдину фізичну теорію, що не залежить від того, які саме з величезної безлічі дослідних даних покладені в основу при її побудові.
У цьому курсі в основу електродинаміки ми покладемо наступні експериментальні факти і закони:
1) дослідний факт існування електричного поля навколо електричних зарядів;
2) експериментальне вираження для сили, що діє з боку електричного поля на точкові заряди;
3) експериментальний закон Кулона;
4) принцип суперпозиції для електричних полів;
5) дослідний факт існування магнітного поля навколо зарядів, що рухаються, (тобто, навколо електричних струмів);
6) експериментальний закон Ампера;
7) експериментальний закон Біо-Савара-Лапласа;
8) принцип суперпозиції для магнітних полів;
9) дослідний факт про замкнутість магнітних силових ліній;
10) експериментальний закон електромагнітної індукції Фарадея;
11) дослідний факт про існування струмів зміщення (змінне електричне поле обумовлює вихрове магнітне поле).
Наступні три параграфи присвячені узагальненню перерахованих дослідних даних і побудові на їхній основі електродинаміки для зарядів і струмів у вакуумі.
§2. Узагальнення дослідних даних про електричне поле.
У цьому параграфі ми теоретично узагальнимо дослідні факти і закони 1)-4), перераховані наприкінці §1. Використовуючи якісне уявлення про електричне поле (див. §1), приступимо до вивчення його кількісних властивостей. Властивості електричного поля, обумовлені деяким зарядом, можна вивчити вимірюючи силу, з яким взаємодіє цей заряд з т.зв. пробним зарядом. Пробним зарядом називається тіло з настільки малим зарядом, що останній практично не спотворює досліджуване з його допомогою електричне поле. Надалі пробний заряд будемо вважати точковим.
Нехай у деякій області простору існує електричне поле, обумовлене деяким наелектризованим тілом, що ми будемо називати джерелом електричного поля. Точку простору в який досліджується (вивчається, спостерігається) поле, будемо називати точкою спостереження. Поміщаючи точкові пробні заряди q і q/ в різні точки спостереження (А и В, наприклад) і вимірюючи сили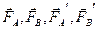 
, що діють на пробні заряди, можна прийти до наступних висновків:
1) відношення величин сил, що діють на різні пробні заряди q і q/, розташовані в одній і тій же точці спостереження не залежить ні від ступеня наелектризованності джерела електричного поля, ні від вибору точки спостереження, а визначається тільки відношенням q/q/ величин пробних зарядів: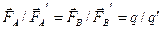 
;
2) відношення величин сил, що діють на той самий пробний заряд у різних точках спостереження визначеного електричного поля, не залежить від величини пробного заряду, а визначається тільки ступенем наелектризованності джерела поля: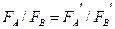 
Легко бачити, що такі емпіричні закономірності можуть спостерігатися тільки тоді, коли сила 
, з якою електричне поле діє на пробний заряд q, дорівнює:
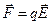(2.1)
де вектор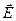 
залежить від електричного стану джерела поля і називається вектором напруженості електричного поля. Помітимо, що експериментальний вираз для сили (2.1) справедлив для будь-яких електричних полів, тому що при його одержанні малося на увазі, що джерело поля може бути будь-яким.
Зауваження. Тому що незалежно від формули (2.1) можна експериментально визначити величину пробного заряду q (вибираючи еталон заряду q0 і користаючись співвідношенням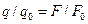 
, що, як ми знаємо, не залежить від електричного поля), тому співвідношення (2.1) фактично є визначенням напруженості електричного поля, тому що воно дає можливість по силі, з яким електричне поле діє на деякий точковий заряд, визначити напруженість електричного поля в кожній точці спостереження.
Експериментальний закон Кулона (1785р.) дає кількісне вираження електричної сили (2.1) для деяких окремих випадків електричних полів. Саме, цей закон говорить, що два точкових нерухомих заряди взаємодіють між собою із силою, що: 1) прямо пропорційна величинам цих зарядів і зворотньо пропорційна квадрату відстані між ними, 2) спрямована уздовж лінії, що з'єднує ці заряди. Наприклад, сила, що діє на заряд q/, розташований у точці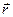 
, з боку заряду q описується формулами:
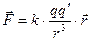чи 
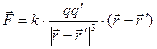(2.2)
у залежності від вибору системи координат, відповідно показаного на малюнках (2.1) і (2.2):
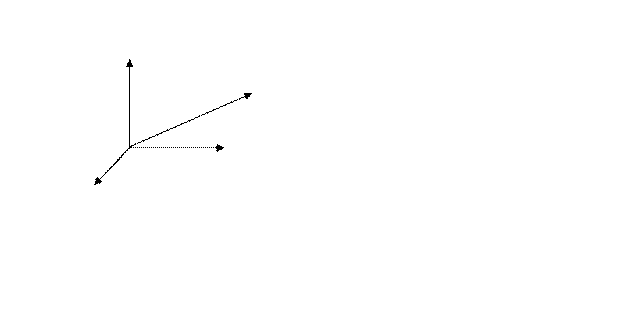
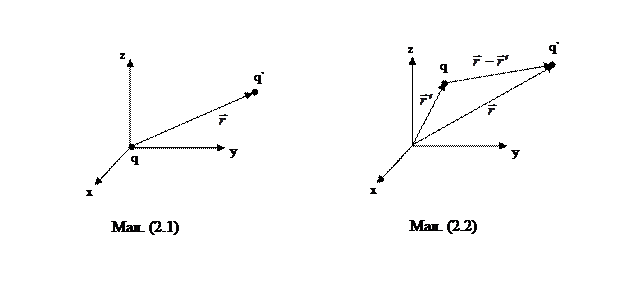
Коефіцієнт пропорційності k у формулах (2.2) не залежить від величини зарядів і відстані між ними; його чисельне значення залежить тільки від вибору системи одиниць виміру. В одиницях СО:
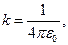(2.3)
де величина e0 називається діелектричної постійною і дорівнює:
e0 = 8.85418782 × 10-12 ф/м (2.3)
Таким чином, в одиницях СО закон Кулона (2.2) має вигляд:
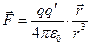
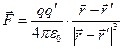(2.2/)
З іншого боку, записуючи згідно (2.1) силу, що діє на заряд q/, у вигляді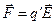 
і порівнюючи з (2.2/) одержуємо вираз для напруженості електричного поля, створеного точковим нерухомим зарядом q у точці спостереження 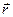(див. рис (2.1) і (2.2)):
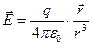
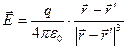(2.5)
Якщо на заряд q діють електричні поля декількох заряджених тіл, то відповідно до принципу суперпозиції сил (див. ч. I, гл. 1) результуюча сила є векторна (геометрична) сума сил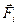 
, що діють з боку всіх зарядів:
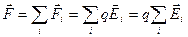(2.6)
де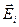 
- напруженість електричного поля, обумовлена i-м зарядом у місці розташування заряду q. Порівнюючи (2.6) з (2.1), приходимо до принципу суперпозиції електричних полів:
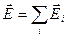(2.7)
тобто результуюча напруженість електричного поля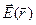 
в довільній точці спостереження 
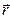, обумовлена декількома зарядами, дорівнює векторній сумі напруженостей електричних полів 
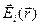у тій же точці 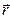, обумовлених окремими зарядами. 
Користуючись принципом суперпозиції (2.7) і формулою (2.5), можна визначити напруженість електричного поля довільної системи точкових зарядів:
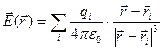
(2.8)
де 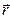- радіус-вектор точки спостереження; 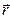i і qi – відповідно радіус-вектор і величина i-го заряду; 
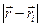- відстань від i-го заряду до точки спостереження. Підсумовування в (2.8) ведеться по всіх зарядах системи.
У класичній електродинаміці відповідно до безупинного характеру електромагнітного поля істотно використовується модельне уявлення про безперервний розподіл зарядів і струмів у просторі. Безперервний розподіл заряду характеризується об'ємною щільністю заряду r, обумовлений формулою:
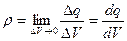(2.9)
де dq є величина заряду, що знаходить у нескінченно малому об'ємі dV. Якщо розподіл заряду у деякому об'ємі V відомий (тобто задана функція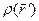 
), то можна розрахувати напруженість 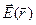електричного поля в довільній точці 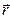в такий спосіб. Розіб'ємо V на елементарні об'єми dV/, положення яких будемо задавати радіусом-вектором 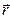/ (див. мал. 2.3).
Згідно (2.5) точковий заряд цього об'єму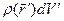 
створює в точці 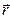електричне поле з напруженістю:
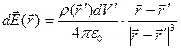(2.10)
Підставляючи (2.10) у формулу:
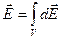(2.7`)
яка є записом принципу суперпозиції (2.7) для випадку безперервного розподілу заряду, одержуємо остаточно:
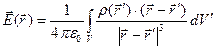(2.11)
Якщо заряди розташовуються в дуже тонкому шарі поблизу поверхні тіла, то часто зручно користатися модельним уявленням про поверхневий розподіл заряду з поверхневою густиною заряду, що визначається подібно (2.9) як заряд одиниці площі даної поверхні:
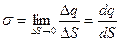(2.12)
де dq – величина заряду елемента поверхні dS. Повторюючи міркування, що призвели до формули (2.11), можна одержати наступний вираз для напруженості електричного поля, створеного поверхневим розподілом заряду:
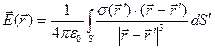(2.13)
де інтегрування ведеться по всій поверхні dS, на якій розподілений заряд.
Результати (2.8), (2.11) і (2.13), що є наслідком закону Кулона і принципу суперпозиції, дозволяють у принципі обчислити електричні поля для довільного розподілу нерухомих зарядів. Однак практичне застосування цих результатів істотно обмежується двома причинами: 1) інтегрування (чи підсумовування) у цих формулах у явному вигляді вдається провести тільки для найпростіших випадків розподілу зарядів (з високим ступенем геометричної симетрії); 2) у деяких задачах (наприклад, при вивченні поля поблизу провідників) розподіл заряду залежить від зовнішнього поля і є невідомою величиною, яку потрібно визначити одночасно з визначенням електричного поля в процесі рішення задачі – у цих випадках формул типу (2.11) явно недостатньо .
Тому, не зупиняючись на виведених формулах, одержимо шляхом математичних перетворень іншу – (відмінну від (2.8), (2.11) і (2.13)) спільний запис закону Кулона і принципу суперпозиції, що виявиться більш зручним для подальших узагальнень і обчислень.
Для цього введемо в розгляд поняття нової інтегральної характеристики електричного поля - потік вектора напруженості електричного поля через замкнуту поверхню. Визначимо спершу цей потік через елементарну площадку dS довільної форми. Як відомо, положення в просторі площадки dS можна задати за допомогою одиничного вектора нормалі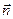 
до площадки (див. мал. (2.4)).
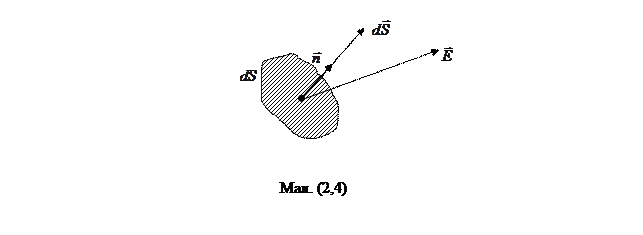
Задати ж одночасно і величину dS і орієнтацію площадки зручно за допомогою вектора довжина якого чисельно дорівнює площі dS (тобто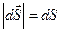 
), а напрямок визначається вектором 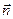(тобто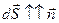 
) – див. мал. (2.4). Потік dN вектора 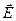через dS визначимо тепер виразом:
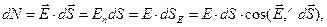(2.14)
де 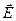- напруженість електричного поля в місці розташування 
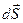, Еn – проекція 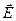на напрямок 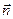(чи ).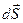 
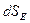– проекція 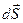на напрямок 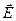(див. мал. (2.4)).
Нагадаємо, що силові лінії (чи лінії 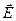) електричного поля проводяться так, щоб задовольнялися умови: 1) напрямок 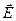у довільній точці збігається з дотичною до силової лінії; 2) число силових ліній, що перетинають одиничну площадку, перпендикулярну 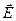, пропорційно величині напруженості поля в струмах площадки. Тому потік dN, визначений формулою (2.14), пропорційний числу силових ліній, що перетинають площадку dS.
Потік вектора 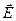через довільну замкнуту поверхню S отримується інтегруванням (2.14) по всієї S, тобто визначається формулою:
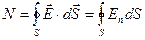(2.15)
де мається на увазі, що вектор 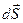(чи 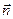) завжди спрямований уздовж зовнішньої нормалі до поверхні S у будь-якій її точці.
У термінах інтегральної характеристики (2.15) закон Кулона і принцип суперпозиції можна об'єднати у вигляді наступної теореми Гаусса-Остроградского: потік вектора індукції напруженості електричного поля через довільну замкнуту поверхню пропорційний величині заряду, що знаходиться усередині цієї поверхні; у системі СО для випадку безперервного розподілу заряду ця теорія записується у вигляді:
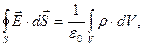(2.16)
де інтегрування в правій частині ведеться по об'єму V, що охоплюється замкнутою поверхнею S. У випадку дискретного розподілу заряду теорема говорить:
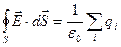, (2.16/)
де підсумовування в правій частині (2.16/) ведеться тільки по тим зарядам, що знаходяться усередині замкнутої S. Теорема Гаусса – Остроградского (теорема Г – О) є інтегральним законом, тому що вона зв'язує повний заряд у деякому об'ємі з загальним потоком через усю поверхню цього об'єму. Не зупиняючись на докладному доказі теореми Г – О (див. курс загальної фізики) приведемо тільки схему цього доказу:
1) підставляючи (2.5) у (2.14), обчислюємо потік 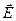поля точкового заряду q через довільну елементарну площадку d:
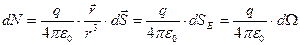, (2.17)
де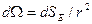 
- величина тілесного кута, під яким спостерігається dS з початку координат, де розташований q;
2) обчислюємо потік через довільну замкнуту поверхню S, усередині якої знаходиться точковий заряд q, інтегруючи (2.17) і використовуючи (2.15):
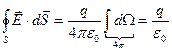, (2.18)
3) доводимо, що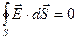 
, якщо заряд q знаходиться поза замкнутою поверхнею;
4) застосовуючи принцип суперпозиції (2.7) і результат (2.18), одержуємо теорему Г – О для дискретного розподілу заряду:
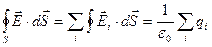
5) шляхом заміни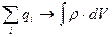 
в останній формулі приходимо в (2.16) для випадку безперервного розподілу заряду.
З приведеної схеми доказу видно, що теорема Г – O є наслідком експериментального закону Кулона і принципу суперпозиції електричних полів.
Для подальшого викладу теорії електричного поля надзвичайно важлива та обставина, що з теореми Г - О (2.16), що є інтегральним співвідношенням, можна за допомогою математичних перетворень одержати як наслідок деяке диференціальне співвідношення. Для цього скористаємося математичною теоремою Г – О з векторного аналізу: для довільного безперервного векторного поля 
справедливе співвідношення:
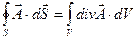, (2.19)
де поверхня S, що охоплює об'єм V.
Застосовуючи (2.19) до лівої частини (2.16), одержуємо:
,
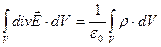відкіля в силу довільності об'єму V одержуємо рівність підінтегральних виразів, тобто:
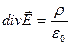(2.20)
Диференціальне співвідношення (2.20) є основним рівнянням електростатики. Воно дозволяє визначити дивергенцію вектора напруженості в будь-якій точці поля по величині густини заряду в тій же точці, причому, поза залежністю від характеру розподілу зарядів в інших точках.
Тепер ми можемо узагальнювати експериментальні дані про електричне поле і прямі наслідки (2.16) і (2.20) з них (які варто вважати емпіричними законами електростатики) до рівня теоретичних законів. Це узагальнення досягається шляхом введення наступної гіпотези: будемо вважати, що співвідношення (2.16) і (2.20), виведені при вивченні взаємодії нерухомих зарядів, справедливі і для довільного змінного електричного поля, обумовленого зарядами, що рухаються. Після прийняття цієї гіпотези диференціальне рівняння (2.20) і його інтегральна форма (2.16) приймає статус одного з основних теоретичних рівнянь електродинаміки. Справедливість цього теоретичного узагальнення підтверджується величезною кількістю дослідів, проведених для перемінних полів.
§3. Узагальнення дослідних даних про магнітне поле.