Принцип непрерывности электрического тока

Одним из основных принципов теории электромагнитного поля является принцип непрерывности электрического тока

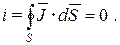
В этом соотношении символ 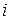означает полный ток сквозь взятую в любой среде замкнутую поверхность 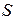, то есть

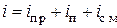и .

И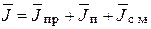з принципа непрерывности электрического тока следует, что линии тока не имеют ни начала, ни конца, то есть являются замкнутыми.

ЭЛЕКТРИЧЕСКОЕ НАПРЯЖЕНИЕ. РАЗНОСТЬ ЭЛЕКТРИЧЕСКИХ ПОТЕНЦИАЛОВ

Электрическое поле кроме векторов 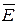и 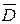характеризуют скалярной величиной, которая называется электрическим напряжением 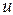и измеряется в вольтах, [ 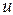] = В .

Для перемещения заряда 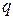в электрическом поле из точки 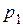в точку 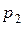необходимо совершить работу

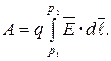
Электрическим напряжением между точкам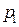и и 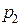называют величину, равную отношению этой работы к перемещаемому заряду

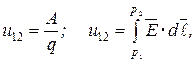
где 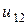‑ электрическое напряжение (или падение напряжения) вдоль заданного пути (рис.1.5).

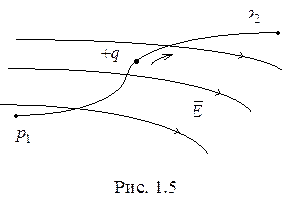
Для электрического поля неподвижных зарядов (электростатического поля) справедливо условие

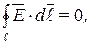
вытекающее из закона сохранения энергии в системе заряженных тел. Следовательно, (рис.1.6),

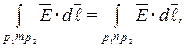
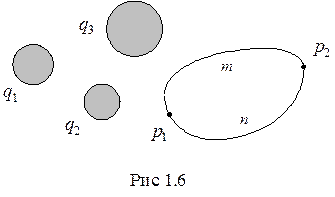
и интеграл 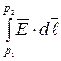зависит только от координат точек 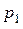и .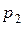

Это обстоятельство позволяет ввести в рассмотрение функцию 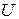, зависящую от положения точки ( 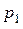) в электростатическом поле:

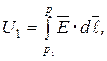
где 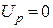Потенциал точки определяется с точностью до некоторой постоянной, зависящей от того, где выбрана точка 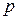нулевого потенциала.

В электростатическом поле напряжение между точкам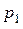и и 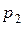можетбыть вычислено как разность потенциалов этих точек:

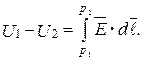
Электрическое поле, для которого справедливо условие 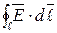= 0, называется потенциальным электрическим полем. При теоретическом исследовании систем, в которых заряженные тела имеют конечные размеры, точка p, выбирается, как правило, на бесконечности. На практике часто U = 0 принимают на поверхности одного из объектов рассматриваемой системы.

Введем понятие поверхности равного потенциала, как поверхности, во всех точках которой потенциал имеет одно и тоже значение. Силовые линии электрического поля перпендикулярны поверхностям равного потенциала. Действительно:

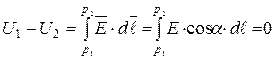
при 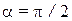и, следовательно, 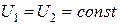(рис.1.7).

ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ

Представим себе проводящее тело конечных размеров, расположенное в диэлектрике с абсолютной диэлектрической проницаемостью 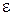. Сообщив некоторый заряд этому телу, приняв потенциал бесконечно удаленных от него точек равным нулю и считая 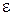среды не зависящей от напряженности электрического поля, получим, что заряд 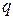и потенциал тела 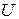пропорциональны друг другу

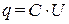или .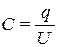

Параметр 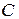называют емкостью данного тела. Единица измерения емкости фарад ([ 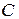] = Ф). Емкость пропорциональна абсолютной диэлектрической проницаемости среды, а также зависит от размеров и формы тела - 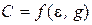. В последнем соотношении символ 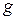имеет смысл некоторого обобщенного параметра, характеризующего геометрические особенности объекта.

При наличии двух проводящих тел с равными по величине и противоположными по знаку зарядами 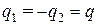(эти условия присущи конденсатору) емкость определится из соотношения

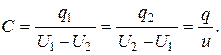
ЭЛЕКТРОДВИЖУЩАЯ СИЛА

Если в электрическом поле 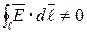, то это означает, что в контуре 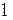существует так называемая электродвижущая сила (э.д.с.) 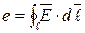([ 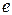] = В). Появление э.д.с. связано с действием не потенциальных полей. В источнике э.д.с. происходит преобразование энергии какого-либо вида (механической, электрохимической, и т.д.) в электрическую. Понятие э.д.с. можно трактовать и таким образом: э.д.с. характеризует способность источника электрической энергии создавать и поддерживать на своих зажимах определенную разность потенциалов.

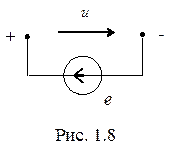
Наиболее распространенные источники э.д.с. - электрические генераторы, аккумуляторы, гальванические элементы. Условное обозначение источника э.д.с. представлено на рис.1.8, причем при разомкнутых зажимах источника .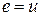

В заключение рассмотрим несколько задач, иллюстрирующих изложенный выше теоретический материал.

Задача 1.Проводящий шар радиусом 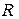с зарядом 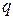расположен в воздухе. Определить выражения и построить графики зависимости электрического смещения 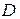, напряженности электрического поля 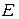, потенциала 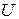в функции расстояния r от центра шара. Рассчитать значение емкости шара 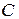. Вычислить значения величин 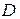, , 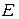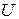на поверхности шара при 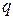= 10^-9 Кл, 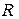= 0,1 м.

Решение. Рассчитаем электрическое поле, создаваемое неподвижным заряженным проводящим шаром, с помощью постулата Максвелла

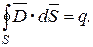
Картина электрического поля имеет вид, представленный на рис.1.9.

Определим характеристики электрического поля в произвольной точке пространства, расположенной вне шара на расстоянии r от его центра. Для этого через выбранную точку проведем замкнутую сферическую поверхность S, центр которой совпадает с центром шара. Внешняя нормаль 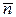к этой поверхности, а значит и вектор 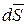, направлены в радиальном направлении и совпадают с направлением вектора .

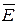Кроме того, в силу симметрии задачи, 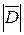имеет одно и то же значение для всех точек поверхности и, следовательно, поток вектора электрического смещения 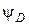может быть определен в виде

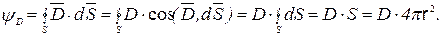
В объеме, ограниченном замкнутой поверхностью 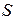, заключен заряд шара 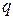. Таким образом, в соответствии с постулатом Максвелла, получим

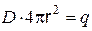или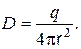

Напряженность электрического поля в воздухе ( 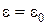) определится из соотношения 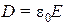в виде

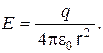
При определении интенсивности электрического поля внутри проводящего шара учтем, что заряд, сообщенный любому проводящему телу, располагается на его поверхности. Поэтому внутри замкнутой поверхности, проведенной через любую точку, лежащую внутри шара, электрический заряд отсутствует. 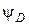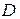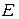Это означает равенство нулю потока через такую поверхность и, следовательно, в любой внутренней точке проводящего шара справедливы равенства = 0 и = 0.

Потенциал 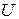точки с координатой r может быть рассчитан из соотношения

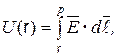
где 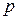‑ точка, потенциал которой принят равным нулю. При решении данной задачи будем считать точку 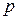расположенной в бесконечности.

Определим потенциал произвольной точки вне шара, выбирая путь интегрирования, совпадающим с силовой линией электрического поля. Тогда

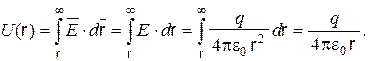
Потенциал произвольной точки внутри шара равен потенциалу на поверхности шара 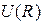, так как внутри шара напряженность поля 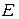= 0,

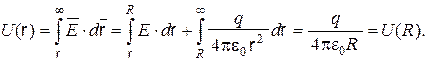
Емкость шара определим, используя выражение для емкости уединенного тела в виде

.

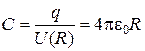Полученные соотношения 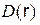, , 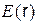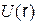дают возможность изобразить графики этих функций на рис.1.10.

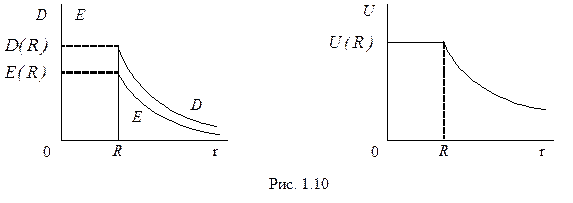
При заданных условиях имеем: 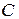= 1,1 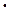10^-11 Ф = 11 пкФ, 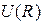= 90 В, 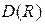= 7,96 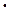10^-9 Кл/м², 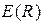= 900 В/м.

Задача 2. Определить величину и распределение заряда на поверхности проводящей пластины, помещенной в однородное электрическое поле с напряженностью 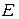(рис.1.11).

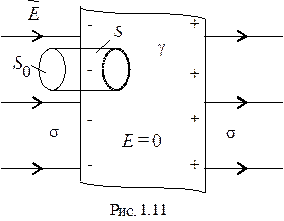
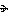Решение. Под действием внешнего электрического поля в электронейтральной проводящей пластине произойдет перераспределение заряда: на левой плоскости раздела воздух-проводник сгруппируются (индуцируются) заряженные частицы, образующие отрицательный заряд, на правой образуется такой же по величине положительный заряд. В результате напряженность электрического поля внутри пластины будет равна нулю.

Определим распределение поверхностной плотности заряда 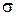([ 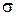] = Кл/м²) по граням пластины, используя постулат Максвелла. Выберем замкнутую поверхность 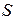в виде цилиндра с основанием 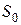, перпендикулярным силовым линиям. Отметим, что

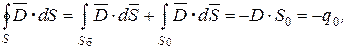
где: 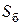‑ боковая поверхность цилиндра, нормаль к которой перпендикулярна вектору 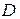. Из последнего соотношения, учитывая связь 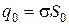, получим 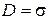. Поэтому, ввиду постоянства 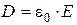в любой точке поверхности 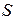, индуцированный заряд распределен по поверхности пластины равномерно с плотностью .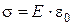