Формула множення ймовірностей подій

Знайдемо ймовірність того, що декілька подій здійснюються одночасно. Нехай події “А” і “В” – незалежні події, тобто ймовірність однієї з них, наприклад,
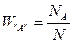не залежить від того, здійснюється чи ні інша подія – “В”. Це зовсім не означає, що події “А” і “В” повинні бути взаємно виключаючими. Навпаки, події “А” і “В” можуть відбуватися одночасно, не виключаючи одна одну.

Розберемо формулу на прикладі:

Нехай є 20 екзаменаційних білетів з фізики, з яких студент вивчив половину (10). В день іспиту він сідає до трамваю та їде. Питання: яка ймовірність того, що в трамваї він отримає квиток з парним номером і на іспиті витягне вивчений білет?

Ясно, що ці дві події незалежні. Легко бачити, що ймовірність отримання парного квитка дорівнює W_”А” =1/2. Бо номера білетів чергуються: непарний, парний, непарний … Ймовірність отримання вивченого білета також дорівнює
W_”В” = 10/20 =1/2. Бо з 20 білетів студент вивчив половину (10). Звідси можливо побачити, що ймовірність складної події W_”АВ” буде дорівнювати множенню ймовірностей кожної з цих подій W_”А” і W_”В”:

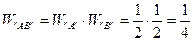
Таким чином, ймовірність спільного здійснення двох або більш незалежних подій дорівнює множенню ймовірностей здійснення кожної з них окремо:

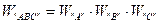(5)

Ця формула є формулою множення ймовірностей.

3. Функція розподілу ймовірностей випадкової неперервної величини

Поширимо наші міркування на випадки, коли величина x приймає неперервний ряд значень в деякому інтервалі
a£ x£b. Причому, зазначений інтервал може бути не обмеженим кінцевими значеннями a и b. Зокрема параметр x може змінюватися від -¥ до +¥, як, наприклад, координати молекули газу для випадку необмеженого середовища.

Швидкість молекул газу також може змінюватися неперервно від 0 до +¥. Наша мета: визначити, яким чином розподіляються молекули газу за швидкостями.

Але перш за все треба зрозуміти, чи означає це питання, що ми хочемо знайти ймовірність того, що у молекул будуть виявлені швидкості, які дорівнюють якийсь строго визначеній швидкості. Та насправді така постановка питання не має змісту.

Число молекул газу у будь-якому об’ємі (окрім нескінченного) завжди має кінцеве значення, тоді як швидкості молекул можуть приймати яке завгодно значення, і число усіх можливих швидкостей наближається до нескінченності. Саме тому число молекул, які приходяться на долю кожного точно заданого математично значення швидкості, дорівнює нулю:

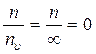
де 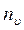– число всіх можливих швидкостей.

Іншими словами, кінцевого числа молекул не достатньо, щоб їх розподілити за кожним фіксованим значенням швидкості.

Внаслідок цього питання про розподіл молекул за швидкостями формулюють так. Скільки молекул (яка частина Dn) мають швидкості, які лежать у деякому інтервалі Du поблизу заданої швидкості u ? Або так. Яка ймовірність того, що будь-яка з молекул газу має швидкість, яка лежить у деякому інтервалі Du поблизу заданої швидкості u ?

Знайдемо закон розподілу частинок за швидкостями, тобто число частинок Dn, швидкості яких лежать у деякому інтервалі Du поблизу заданої швидкості u . Очевидно, що число Dn тим більше, чим більше сам інтервал Du і чим більше число частинок n в усій системі:

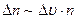
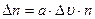(6)

де а – це коефіцієнт пропорційності.

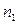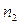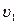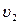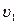
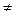
Зрозуміло, що кількості молекул D і D , швидкості яких лежать в однакових інтервалах D = D , але поблизу різних швидкостей 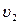, не будуть однаковими. Так само, як, наприклад, відносна кількість людей, вік яких лежить в інтервалі 2 роки, але поблизу віку 20 років і 80 років (тобто від 20 років до 22 і від 80 до 82) не буде однією і тією ж самою.

Отже коефіцієнт пропорційності у формулі (6) являє собою функцію від швидкості:

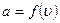Þ

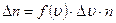(7)

Частіше цю формулу записують у вигляді:

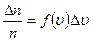(8)

У цій формулі Dn/n – це відносне число частинок (в одиниці об’єму газу), швидкості яких лежать в інтервалі від u до u + Du поблизу швидкості u.

Якщо перейти до нескінченно малих інтервалів du, то формулу (8) перепишемо:

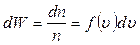(9)

де 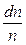– ймовірність того, що будь-яка з молекул газу, що знаходиться в одиниці об’єму, має швидкість в інтервалі du поблизу швидкості u.

Функція ¦(u) називається функцією розподілу. Фізичний зміст функції ¦(u) випливає з формули:

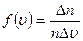(10)

– це ймовірність того, що будь-яка з молекул газу, (що знаходиться в одиниці об’єму газу) має швидкість, яка лежить в одиничному інтервалі швидкостей поблизу обраної швидкості u. Тому функція ¦(u) називається густиною ймовірності.

В математиці функція ¦(u) мала б такий зміст: функція розподілу ймовірностей неперервно змінної випадкової величини u. У фізиці ми опускаємо слово “ймовірність” і кажемо просто: функція розподілу швидкостей (функція розподілу молекул за швидкостями).

Залежність величини 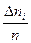(ймовірності того, що у будь-якої молекули виявиться швидкість з інтервалу D 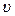поблизу заданої швидкості 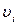) від величини самої швидкості 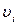наглядно характеризує гістограма, яка будується за таким принципом:

1. Проводять експеримент, у якому фіксуються числа молекул D 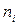, швидкості яких лежать в однакових за величиною інтервалах 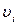D = D 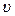, але поблизу різних швидкостей ( ).

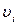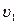
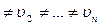2. Вгору від осі оu відкладають вертикальні прямокутники, ширина котрих дорівнює D 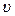, а висота – 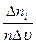відповідно до потрібних нам значень швидкості .

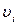Очевидно, що площі побудованих прямокутників дорівнюватимуть 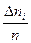, тобто відносному числу молекул, швидкість яких лежать в інтервалі D 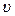поблизу швидкості .

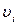При 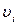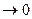ступінчата лінія, яка обмежує гістограму перетворюється на неперервну гладку криву. Ця крива являє собою графічне відображення аналітичної залежності :

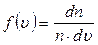
Знайдемо тепер умови нормування функції розподілу. Як ми вже знаємо, ймовірність того, що швидкість молекули знаходиться у межах від u до u +du поблизу швидкості u, через функцію розподілу визначається так:

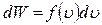
Якщо про інтегрувати цей вираз в інтервалі всіх можливих значень швидкості 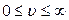, то, очевидно, ми знайдемо ймовірність виявлення у молекули швидкості будь-якої з можливих. Ясно, що ця подія достовірна (тому що у молекули завжди є швидкість). Таким чином:

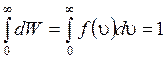(11)

Формула (11) являє собою умову нормування функції розподілу.

У геометричній інтерпретації вираз (11) означає, що площа, обмежена графіком функції розподілу і віссю оu, дорівнює одиниці, як і площа гістограми.