Determination of the resulted length of physical pendulum

Purpose of work: study of laws of oscillation physical and mathematical pendulums.

Task: experimentally and theoretically to find resulted length of physical pendulum.

Devices and equipments: physical pendulum, mathematical pendulum, straightedge, stop-watch. The experimental setting (fig.10.1) consists of physical 1 and mathematical 2 pendulums.

Figure 10.1

Length of mathematical pendulum can be fluently changed, reeling it in 5 and to fix spirally 6.

Theoretical part

A physical pendulum is a body which can be revolved relatively of arbitrary horizontal axis, that not go through the center of mass. Under the action of moment of force mg, the arm of which is L·sinα, a body is revolved round the point of hang up O (fig.10.2). L is distance from a point O rotation (points of hang up) to the point of C - center of mass of body. Write down the fundamental equation of the rotational motion dynamics

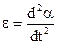, (10.1) I is a moment of inertia of body, is angular acceleration. A sign does minus take into account, that the moment of force of mg is diminished by a corner α.

Figure 10.2

Thus, get differential equation of undamped oscillation of the physical pendulum

. (10.2)

At small corners α (less 5^о) is it possible, that sin α = α. Get

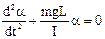(10.3) Comparing this equation to general equation of undamped harmonic oscillations

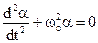, (10.4)

get cyclic frequency and period of oscillation of the physical pendulum

(10.5)

Thus, the period of oscillation of the physical pendulum depends on position of point of hang up O and forms of body, that to its moment of inertia in relation to this point.

For a mathematical pendulum, which is a material point, suspended on a weightless unstretching thread long L, moment of inertia is , . Consequently the period of oscillation of the mathematical pendulum depends only on length of thread

. (10.6)

The resulted length of L_res of physical pendulum is such length of mathematical pendulum the period oscillation of which equals the period of oscillation of the physical pendulum. From (10.5) and (10.6) we have

. (10.7)

A moment of inertia of peg (fig.10.1) is taking into account a theorem Steiner

. (10.8)

Thus, from (10.7) and (10.8) get the theoretical value of the resulted length

. (10.9)

Find the theoretical value of period of oscillation of the physical pendulum from (10.5) and (10.8)

. (10.10)

Practical part

1. Take off a physical pendulum from a bracket.
2. By a line to measure general length of b peg.
3. Set a supporting prism 3 in the distance and a = 20 + N of see from his middle and to fix its spirally 4. N is a number of educational brigade.
4. Hang up a physical pendulum.
5. Decline mathematical and physical pendulums on a corner approximately 5^о and to release.
6. By sight to watch after synchronousness of oscillations of both pendulums. In case, if the period of mathematical pendulum more than (less) physical, to decrease (to increase) length of thread of mathematical pendulum.
7. To repeat points 5, 6 to coinciding of periods of oscillations of pendulums, that synchronous oscillation during not less than 20 oscillations.
8. To measure time t of 20 oscillations of pendulums and to find a period .
9. By a line to measure length of mathematical pendulum from the point of hang up to the center of peg. It will be experimental value of the resulted length of physical pendulum of L_exp .
10. Expect the theoretical values of the resulted length after a formula (10.8) and period after a formula (10.10).
11. Compare the experimental and theoretical values of resulted length and to the period, writing down them in a table 10.1.

Table 10.1

Ltheory , sm	Lexp , sm	Ttheory , s	Texp , sm

12. Expect the error of L_theory.

Control questions

8. What is physical pendulum?

9. What is mathematical pendulum?

10. Get differential equation of free harmonic oscillation of the physical pendulum.

11. Get the period of oscillation of the physical pendulum.

12. Get the period of oscillation of the mathematical pendulum.

13. Give determination of the resulted length of physical pendulum.

14. Get expression for the resulted length of physical pendulum.

Literature

1 Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80.

2. Лапотинський І.Е., Зачек І.Р. Фізика для інженерів.- Львів: Афіша, 2003.-С.

3. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.196-199.

4. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.

Translator: S.P. Lushchin, the reader, candidate of physical and mathematical sciences.

Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.

Approved by the chair of physics. Protocol № 6 from 30.03.2009 .

ЛАБОРАТОРНА РОБОТА № 43.4

ОБОРОТНИЙ МАЯТНИК

Мета роботи: вивчити методику визначення прискорення вільного падіння за допомогою оборотного маятника .

Завдання:. виміряти прискорення вільного падіння.

Прилади й знаряддя: оборотний маятник, секундомір.

Експериментальна установка зображена на рисунку 11.1. На вертикальній стійці 1, яка встановлена на основі 2 з розташованим на ній електронним секундоміром 3, закріплені два кронштейни: нижній рухомий 4 з фотоелектричним датчиком 5 та верхній нерухомий 6. На верхній нерухомий кронштейн 6 підвішується оборотний маятник, який уявляє собою

Рисунок 11.1 стальний стержень, на якому закріплені опорні призми А і B та рухомі вантажі C и D.

Теоретична частина

Фізичний маятник – це тіло, яке може обертатись відно­сно довільної горизонтальної осі, яка не прохо­дить через центр маси.

Оборотний маятник – це фізичний маятник, який має дві точки коливання, при послідовному підвішуванні за які періоди коливань маят­ника буде однаковими..

У нашому випадку це дві точки, що відповідають положенням призм А і В. При закріпленні оборотного маятника на призмах А и B шляхом переміщення вантажів C і D вздовж його осі можна, змінюючи момент інерції маятника, домогтися рівності періодів його коливань:

, (11.1)

де I_A і I_B – моменти інерції маятника відносно осей, які проходять через точки A і B; a і b – відстань від центра мас до відповідної осі коливань.

Теоремою Штейнера стверджує, що момент інерції I тіла відносно будь-якої осі обертання дорівнює моменту інерції I_o цього тіла відносно осі, що проходить через центр маси тіла і паралельна заданій плюс добуток маси тіла на квадрат відстаніміж осями. Маємо

; , (11.2)

де I₀ – момент інерції маятника відносно осі, яка проходить через його центр тяжіння і яка паралельна осі коливань.

Підставляючи (11.2) в (11.1), отримаємо формулу для розрахунку прискорення вільного падіння g:

(11.3)

Таким чином, для визначення прискорення вільного падіння за допомогою оборотного маятника, не­обхідно виміряти дві величини: відстань між опорними призмами (a+b) та період коливань T=T_A=T_B фізичного маятника.

Практична частина

1. Увімкнути шнур живлення приладу в мережу і натиснути вимикач "Сеть".

2. Перевірити роботу індикаторів та лампочок фотоелектрично­го датчика: індикатори електронного секундоміра та лічильника кількості коливань (періодів) повинні висвічувати "0" в усіх розрядах, а лампочка фотоелектричного датчика – світитися.

3. Закріпити вантаж C на відстані s = (5+n) см від призми A, а вантаж D – на відстані h=1 см від призми Б, де n – номер навчальної бригади.

4. По шкалі, нанесеній на стержні, знайти відстань L між призмами.

5. Підвісити маятник на призмі A на верхньому нерухомому кронштейні.

6. Нижній кронштейн установки перемістити таким чином, щоб стержень маятника перетинав оптичну вісь фотоелектри­чного датчика.

7. Відхиливши маятник від положення рівноваги на кут 5÷10°, дати йому можливість здійснювати вільні коливання.

8. Натиснути вимикач "Сброс".

9. Виміряти час N=10 повних коливань маятника, для чого після підрахунку 9 повних коливань натиснути на секундомірі вимикач "Стоп".

10. Розрахувати період T коливань маятника за формулою:

, (11.4)

де t – загальний час N коливань.

11. Розрахувати період коливань T_A при різних положеннях h вантажу D на стержні маятника у відповідності з пп. 7-10. Положення вантажу D на стержні маятника змінювати через кожну поділку основної шкали, тобто через 1 см. При цьому положення вантажу C залишається незмінним. Результати вимірювань занести до таблиці 11.1.

Таблиця 11.1

№	h, см	TA, с	TB, с
…	…
n

12. Підвісити маятник на призму B.

13. Підняти нижній кронштейн з фотоелектричним датчиком у відповідності з п. 6.

14. Визначити період T_B коливань маятника для різних положень вантажу D на стержні Е у тих самих межах та з тим самим числом вимірювань. Результати вимірювань занести до таблиці 11.1.

15. За даними таблиці 11.1 побудувати на міліметровому папері графіки залежностей періодів T_A і T_B коливань від положення h вантажу D на стержні маятника: T_A=f(h) и T_B=f(h). Точка перетину кривих визначить координату рухомого вантажу D на стержні маятника, при якому значення періодів будуть однаковими Т_A=Т_B=T.

16. Для цього положення вантажу D у відповідності з пп. 7-10 знайти періоди коливань маятника відносно призм A і B. Вимірювання періодів коливань відносно кожної призми проводити по 3 рази. Результати вимірювань занести до таблиці 11.2

Таблиця 11.2

№	с	с	,с2	с	с	с2
	, с	—	, c2	, с	—	, с2

17. Знайти шуканий період коливань маятника за формулою:

(11.5)

18. За формулою (11.3) розрахувати прискорення вільного падіння . Результат представити у вигляді:

де Δg – абсолютна похибка визначення g, яку знаходять за формулою

, (11.6)

де: Δπ – розраховують як похибку табличної величини;

ΔL – розраховують як похибку прямого одиничного вимірювання.

Абсолютну похибку вимірювання знаходять за формулою:

, (11.7)

де ΔT_A, ΔT_B визначають як похибки прямих багаторазових вимірювань.

19. Порівняти отримане експериментальне значення з довідковим м/с².

20. Зробити висновок.

Контрольні запитання

1. Що таке прискорення вільного падіння? Який напрямок прискорення вільного падіння та від чого воно залежить?

2. Дати визначення фізичного маятника.

3. Вивести формулу для періоду коливань фізичного маят­ника.

4. Дати визначення приведеної довжини фізичного маятника?

5. Сформулювати теорему Штейнера.

Література

1. Савельев И.В. Курс общей физики, том I. Механика, колебания и волны, молекулярная физика.
2. Сивухин Д.В. Общий курс физики, том I. Механика.

Інструкцію склав асистент каф. фізики ЗНТУ Сейдаметов С.В.

Laboratory Work № 43.4