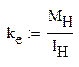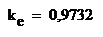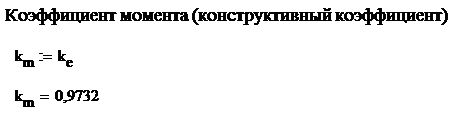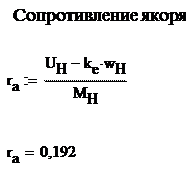Федеральное государственное бюджетное образовательное учреждение высшего образования

«тюменский индустриальный университет»

ТОБОЛЬСКИЙ ИНДУСТРИАЛЬНЫЙ ИНСТИТУТ (филиал)

Кафедра электроэнергетики

Лабораторная работа

«Сопоставительный анализ переходных процессов в ДПТ НВ при пренебрежении и учете электромагнитной постоянной времени»

по дисциплине

«Электрический привод»

Выполнил студент

группы ЭСбз-13

Низовских Е.А.

Проверил:

Рысев П.В.

доцент, к.т.н.

Тобольск 2016

Цель работы: Ознакомиться с моделями ДПТ и сравнить результаты, полученные на различных моделях.

ОПИСАНИЕ ИССЛЕДУЕМЫХ МОДЕЛЕЙ

В данной лабораторной работе используются две модели двигателя постоянного тока:

1) Модель без учета электромагнитных инерционностей – двигатель представлен вращающимся телом. Модель описывается уравнением

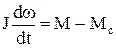, (1)

где J – момент инерции, кг∙м²;

М – вращающий момент, Н∙м;

М_с – момент сопротивления, Н∙м;

ω – угловая скорость вращения ротора двигателя.

Механическая характеристика двигателя имеет вид

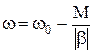, (2)

где ω₀ – угловая скорость холостого хода;

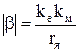– жесткость механической характеристики двигателя,

здесь k_e, k_м – конструктивные коэффициенты двигателя;

r_я – сопротивление обмотки якоря, Ом.

Уравнениям (1) и (2) соответствует структурная схема, представленная на рисунке 1.

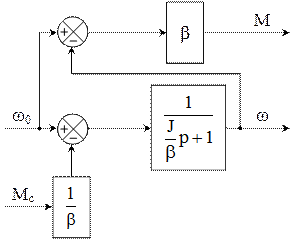
Рисунок 1 – Структурная схема одномассовой модели.

2) Модель ДПТ, учитывающая электромагнитную инерционность – составлена на основании уравнений

(3)

где u_я – напряжение на выводах обмотки якоря, В;

i_я – ток в обмотке якоря, А;

r_я – сопротивление обмотки якоря, Ом;

L_я – индуктивность обмотки якоря, Гн;

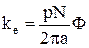– электромагнитный коэффициент;

k_м – электромеханический коэффициент (в СИ k_м=k_e);

здесь р – число пар полюсов двигателя;

N – число витков в обмотке якоря;

a – число параллельных ветвей в обмотке якоря;

Ф – магнитный поток пересекающий обмотку якоря.

Системе уравнений (2) соответствует структурная схема, представленная на рисунке 2.

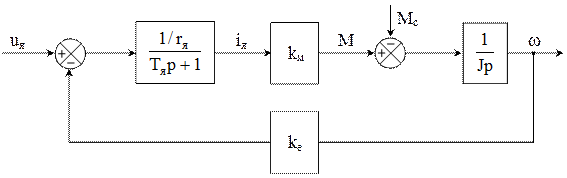
Рисунок 2 – Структурная схема модели, учитывающей электромагнитную инерционность.

ОПИСАНИЕ ЛАБОРАТОРНОЙ РАБОТЫ

В лабораторной работе рассматриваются две модели электропривода: одномассовая и двухмассовая.

Одномассовая модель представляет собой один дискретный инерционный элемент (рис. 3).

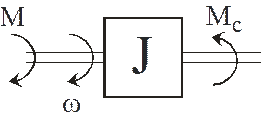
Рисунок 3 – Одномассовая модель электропривода

Структурная схема одномассовой модели электропривода постоянного тока собранная в приложении Simulink приведена на рисунке 4.

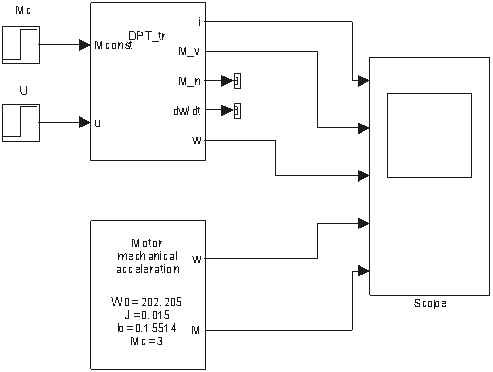
Рисунок 4 – Структурная реализации одномассовой модели электропривода.

Источники ступенчатого сигнала 1 и 2 служат для задания момента сопротивления и напряжения на входе подсистемы 3, представляющей модель ДПТ учитывающую электромагнитные инерционности. Подсистема 4 содержит модель ДПТ не учитывающую электромагнитные инерционности. Виртуальный осциллограф 5 служит для вывода результатов моделирования на экран.

Структурные схемы подсистем 3 и 4 представлены на рисунках 5 и 6 соответственно.

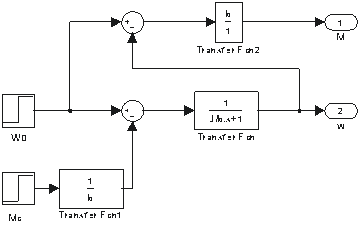
Рисунок 5 – Структурная схема подсистемы одномассовой модели

(без учета электромагнитной инерционности).

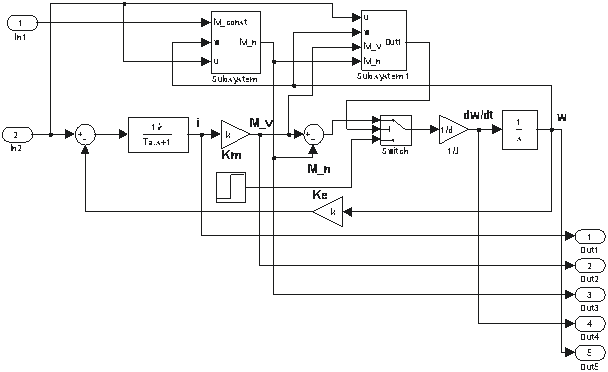
Рисунок 6 – Структурная схема подсистемы модели,

учитывающей электромагнитную инерционность.

Двухмассовая схема состоит из двух дискретных инерционных элементов, соединенных упругой связью – рисунок 7.

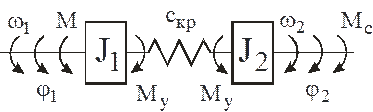
Рисунок 7 – Двухмассовая модель электропривода.

Структурная схема двухмассовой модели электропривода постоянного тока собранная в приложении Simulink приведена на рисунке 8.

Рисунок 8 – Структурная схема реализации двухмассовой модели

электропривода.

ВАРИАНТЫ ЗАДАНИЙ

Таблица 1

Вариант	Двигатель №1	Двигатель №2

Примечание: Параметры двигателей приведены в приложении 1.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Рассчитать исходные данные, необходимые для моделирования:

– коэффициенты k_е и k_м

;

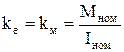– номинальная угловая скорость

;

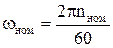– угловая скорость холостого хода

;

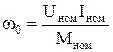– сопротивление якоря

;

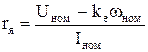– абсолютная жесткость механической характеристики

.

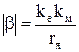2. Ввести параметры двигателя в окне модели, учитывающей электромагнит­ную инерционность (момент сопротивления принять равным номинальному М_с=М_ном).

3. Ввести параметры в окне модели, не учитывающей электромагнитную инерционность.

4. В окне задания параметров расчета (Ctrl-E) выбрать метод Рунге-Кутта четвертого порядка с постоянным шагом в 3-5 раз меньше электромагнитной постоянной. Время моделирования ус­танавливается в зависимости от длительности переходного процесса (на графике должно быть видено завершение переходного процесса).

5. Выполнить моделирование и снять в отчет графики тока якоря, вращающего мо­мента, угловой скорости на выходе модели, учитывающей электромагнитные переходные процессы и графики вращающего момента и угловой скорости одномассовой модели.

6. Сравнить характер переходных процессов, полученных на моделях с учетом и без учета электромагнитной инерционности.

7. Повторить действия пунктов 1-5 для второго двигателя.

8. Определить время регулирования скорости и результаты свести в табл. 2.

Таблица 2

	Модель, не учитывающая электромагнитную инерционность	Модель, учитывающая электромагнитную инерционность
tр, с	Двигатель №1
Двигатель №2

9. Сравнить полученные результаты для обоих двигателей, сделать выводы.

10. Снять графики для двухмассовой модели электропривода.

11. Проанализировать зависимость характера работы электропривода от коэффициента упругости упругого элемента.

СОДЕРЖАНИЕ ОТЧЕТА

1. Цель работы.

2. Исходные данные (вариант, параметры двигателей).

3. Структурная схема модели.

4. Результаты моделирования для двигателя №1 (графики).

5. Результаты моделирования для двигателя №2 (графики).

6. Определение времени регулирования для обеих моделей.

7. Выводы.

ВОПРОСЫ К ЗАЩИТЕ

1. Система уравнений, описывающая двигатель постоянного тока.

2. Чем объясняется затягивание переходного процесса в модели, учитывающей электромагнитную инерционность?

3. От чего зависит характер переходного процесса в двигателе постоянного тока.

4. Механическая характеристика двигателя постоянного тока, жесткость механической характеристики.

ПРИЛОЖЕНИЕ 1 – Параметры двигателей.

№	Тип двигателя	Мном, Н∙м	nном, об/мин	Рном, кВт	Uном, В	Iном, А	J, кг∙м2	Тм, с	Тя, с
	ПБВ-100М	7,16		0,75			0,01	10,3∙10-3	5,3∙10-3
	ПБВ-100L	10,5		1,1			0,013	7,6∙10-3	5,75∙10-3
	ПБВ-112S			1,1		31,5	0,035	13,2∙10-3	6,75∙10-3
	ПБВ-112M	17,5		1,1			0,042	10,1∙10-3	7,3∙10-3
	ПБВ-112L			1,1			0,049	8,6∙10-3	7,65∙10-3
	ПБВ-132М			2,2			0,188	14,2∙10-3	7,35∙10-3
	ПБВ-132L	47,7		3,0			0,238	12,3∙10-3	7,85∙10-3
	ПБВ-160М	76,4		4,0		78,5	0,242	8,5∙10-3	10,6∙10-3
	ПБВ-160L			5,5	78,5		0,242	7,9∙10-3	11,8∙10-3
	ПФВ-160S	143,2		7,5			0,194	9,9∙10-3	2,25∙10-3
	ПФВ-160M						0,242	8,5∙10-3	1,6∙10-3
	ДК1-1,7-100АТ	1,7		0,18			2,1∙10-3	25∙10-3	2,5∙10-3
	ДК1-2,3-100АТ	2,3		0,24		7,5	2,7∙10-3	20∙10-3	3∙10-3
	ДК1-3,5-100АТ	3,5		0,37		7,5	2,85∙10-3	15∙10-3	3,5∙10-3
	ДК1-5,2-100	5,2		0,55		6,5	3,9∙10-3	10∙10-3	5,3∙10-3
	ДПУ87-75-23	0,7		0,075		4,5	0,21∙10-3	9∙10-3	1,5∙10-3
	ДПУ127-220-1-30	2,1		0,22			2,8∙10-3	25∙10-3	3,2∙10-3
	ДПУ127-450-2-57	4,3		0,45			4,9∙10-3	15∙10-3	3,8∙10-3
	4ПБМ112МГ04	6,2				5,7	0,015	96,7∙10-3	5,9∙10-3
	2ПБМ112LГ04	6,11		0,9		10,1	0,018	68,8∙10-3	6,036∙10-3

При выполнении лабораторной работы использовать:

Тип двигателя ПБВ-160 М

Исходные данные

М_ном, Н∙м 76,4

n_ном, об/мин 500

Р_ном,к Вт 4

U_ном, В 66

I_ном, А 78,5

J, кг∙м² 0,242

Т_я, с 10,6∙10^-3

Расчеты

Коэффициент противоэдс