Методические рекомендации к выполнению

Квантование и дискретизация являются теми операциями, в результате выполнения которых аналоговый сигнал (сигнал непрерывный по значениям и времени) заменяется дискретным сигналом по значениям и времени. На практике эти две операции выполняются прибором, получившим название «аналого-цифровой преобразователь». Термин «цифровой» в данном случае означает, что на выходе данного прибора сигнал представлен в кодированной форме, т.е. каждый уровень квантования заменяется соответствующей этому уровню кодовой комбинацией двоичного безизбыточного кода.

Для выполнения операции квантования должно быть известно (или задано) число ступеней квантования (или уровней квантования) и параметры каждой ступени: максимальное и минимальное значение кванта, значение уровня квантования. Размер кванта можно получить, разделив диапазон изменения сигнала на заданное вариантом число уровней квантования.

Пусть исходный сигнал описывается функцией времени s(t)=50е^-0,1t у.е. (условных единиц), tÎ[0, 3,8с]. Данная функция времени является монотонно убывающей, следовательно,

S_макс=S(t=0)=50 у.е., S_мин=S(t=4)=50e^-0,1·3,8=34,2 у.е.,

и диапазон изменения сигнала составит D_S=(S_макс-S_мин)=15,8 у.е.

Указание: В вариантах задания 3-6, 9и 10 для нахождения диапазона изменения сигнала необходимо произвести математическое исследование функции сигнала на максимум.

Перед выбором числа уровней квантования рассчитаем суммарную погрешность воспроизведения. Допустим, что суммарная погрешность задана равной 1%от максимального значения сигнала: δ_∑=0,01·50=0,5 у.е.

Известно, что максимальное значение ошибки квантования равномерного приближения при выборе уровня квантования в середине ступени квантования равно половине кванта (ступени квантования) Δs: δ_кв=Δs/2.

Размер кванта можно получить, разделив диапазон изменения сигнала на число уровней квантования. Поскольку предполагается кодирование уровней квантования двоичным кодом, то число уровней квантования М следует выбирать на основе соотношения М=2^m-1, где m – разрядность кода (комбинация из нулей не используется для передачи значения уровня).

Если принять число уровней квантования M=15 (m равно 4), то

Δs= D_S/15=15,8\15»1,053 у.е.

В этом случае ошибка квантования d_кв составит 0,527 у.е. Поскольку d_кв>δ_∑=0.5 у.е., то значение M=15 является неприемлемым.

Выберем число уровней квантования M=31 (m равно5). В этом случае:

Δs= D_S/M=15,8/31»0,51 у.е., d_кв»0,255 у.е.< 0,5 у.е.

Примем значение ступени квантования Δs=0,5 у.е. Уменьшение значения Δs по сравнению с расчетным уменьшит значение погрешности до d_кв=0,25 у.е.

Шкалу квантования построим, начиная с наибольшего значения сигнала.

Для первого кванта: верхняя граница S_1max=50 у.е., нижняя граница S_1min= S_1max-Δs=50-0б5=49,5 у.е., уровень квантования S₁= S_1max-Δs/2=49,75 у.е. Таким образом, если значение сигнала S лежит в пределах 50 у.е.³ S > 49,5 у.е., то оно заменяется уровнем 49,75 у.е.

Для второго кванта: S_2max=49,5 у.е., S_2min=49,0 у.е., уровень квантования S₂=49,25 у.е.; значение сигнала 49,5 у.е.³ S > 49,0 у.е. заменяется уровнем 49,25 у.е.

Для последней (31-й) ступени квантования граничные значения кванта и значение уровня квантования;

S₃₁=S₁-30*Δs=49,75-30*0,5=34,75 у.е.,

S_31max=S_1max+Δs/2=34,75+0,25=35 у.е.,

Так как это последняя ступень квантования, то все значения сигнала S<S_31max=35 у.е. заменяются значением уровня S₃₁=34,75 у.е.

Для 30-й ступени квантования S_30max=35,5 у.е., S_30min=35,0 у.е., уровень квантования S₂=35,25 у.е.; значение сигнала35,5 у.е.³ S >35,0 у.е. заменяется уровнем 35,25 у.е.

Шкалу квантования можно представить таблицей.

Таблица квантования

№ кванта	Верхняя граница кванта	Нижняя граница кванта	Уровень квантования	Кодовая комбинация
	50,0	49,5	49,75
	49,5	49,0	49,25
	49,0	48,5	48,75
	48,5	48,0	48,25
. . .
	35,5	35,0	35,25
	35,	-	34,75

В этой таблице также представлены кодовые комбинации, соответствующие уровням квантования.

Переходим к расчету процесса дискретизации. Прежде всего, необходимо определить допустимую погрешность дискретизации как

δ_д=δ_∑- δ_кв=0,25 у.е.

Значение шага дискретизации определяется заданной моделью воспроизводящей функции, но независимо от того, задан ли способ воспроизведения ступенчатая экстраполяция (шаг дискретизации 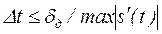) или ступенчатая интерполяция (шаг дискретизации 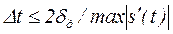), необходимо определить абсолютное максимальное значение первой производной сигнала .

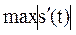Первая производная сигнала s(t)=50е^-0,1t равна: 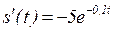. Функция 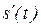является монотонно возрастающей: 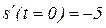, , 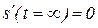следовательно, .

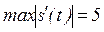Указание: В вариантах задания 3-6, 9и 10 для нахождения абсолютного максимального значения первой производной сигнала необходимо произвести математическое исследование первой производной.

Если задан способ воспроизведения ступенчатая экстраполяция, то шаг дискретизации равен

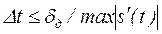=0,25/5=0,05 с.

Таким образом, на интервале задания сигнала (0; 3,8 с) необходимо взять 3,8/0,05=76 отсчетов.

Для графического изображения процессов квантования, дискретизации и воспроизведения выбираем интервал времени, на котором имеет место наибольшая скорость изменения значений сигнала. В данном случае это интервал [0, 4Dt]. Расчеты по построению процессов сведем в таблицу.

Точки взятия отсчетов сигнала, ti (в секундах)	Значения сигнала в точках отсчета S(ti) (условные единицы)	Каким уровнем квантования заменяется (условные единицы)
0,00	50,00	49,75
0,05	49,75	49,75
0,10	49,50	49,25
0,15	49,26	49,25

На рисунке жирными линиями отмечены отсчеты сигнала S(t_i). Воспроизводящая функция S^*(t) изображена прерывистыми линиями.

Оценим погрешности воспроизведения. Наибольшее значение погрешности воспроизведения на первом интервале дискретизации имеет место при t=0 (в начале интервала) и равно 50-49,75=0,25<δ_∑=0,5 у.е. Для второго интервала дискретизации наибольшее значение погрешности воспроизведения имеет место на конце интервала дискретизации: 49,75-49,5=0,25<δ_∑=0,5 у.е. Для третьего интервала дискретизации наибольшее значение погрешности воспроизведения имеет место в начале интервала дискретизации: 49,5-49,25=0,25<δ_∑=0,5 у.е. Таким образом, погрешность воспроизведения не превышает допустимого значения.

Для передачи по каналу связи квантованные отсчеты подвергаются кодированию простым (т.е. безизбыточным) двоичным кодом. Каждому уровню квантования должна соответствовать своя кодовая комбинация. Для кодирования 32 уровней необходим 5-ти разрядный двоичный код (см. таблицу квантования, m≥log₂M= log₂32=5).

Предъявим требования к полосе пропускания канала связи, если в качестве линейного сигнала будет применен код без возврата к нулю. На передачу кодированного отсчета в реальном времени предоставляется временной интервал, равный шагу дискретизации Δt=0,05 с. Часть этого интервала необходимо зарезервировать для передачи синхронизирующей и контролирующей ошибки информации. Допустим, что для передачи 5 информационных разрядов (т.е. разрядов, несущих информацию о значении отсчета), предоставлено 0,03 с. Тогда длительность одного битового интервала составит τ=0,03/5=0,006 с, т.е. скорость передачи 1/0,006»167 бит/с, а полоса пропускания канала связи Δf=1/τ=167 Гц.