Лекция 28. Средства измерений как система
Тема 14. Автоматизированные информационные измерительные системы
Лекция 28. Средства измерений как система
В принципе, любое техническое устройство может рассматриваться как система — вопрос лишь в степени детализации. При использовании системных понятий для описания какой-либо части объекта (объективной реальности) эту часть отделяют от окружения таким образом, чтобы в поле рассмотрения осталось лишь конечное число наиболее важных взаимодействий с этой средой. Последние могут носить характер вещественных и/или энергетических связей, выражаемых в обмене информацией (рис. 14.1 а). Если внимание исследователя концентрируется только на обмене информацией между рассматриваемым объектом и окружающей его средой, то об объекте говорят как об информационной системе. Выдаваемая этой системой информация по форме и содержанию зависит от входной информации.
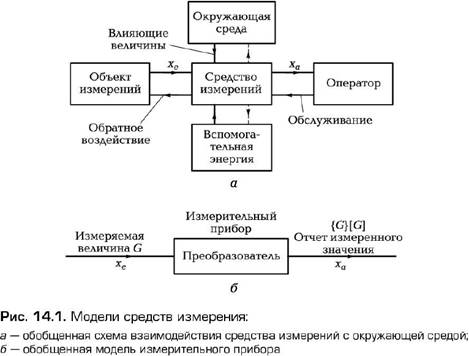
Модель измерительного преобразователя в виде передаточного звена, приведенная на (рис. 14.1 б), является примером простейшего схематичного изображения информационной системы. К этой системе может подводиться информационный поток в виде множества входных величин (xe1…, xen). В результате их обработки в системе (путем выполнения операций, описываемых определенными математическими зависимостями) на выходе системы выдаются соответствующие выходные величины (xa1…, xan).
Определенные связи (зависимости), существующие между входными и выходными величинами, именуют передаточными свойствами (характеристиками) системы. Одинаковым системам присущи одинаковые свойства (характеристики).
Одним из преимуществ системного подхода к исследованию объектов является возможность приложения характеристик, измеренных у одной системы, к другой системе, отличающейся своим построением от первой, но имеющей такие же передаточные свойства. При рассмотрении средств измерений как кибернетических систем удается глубже проникнуть в их суть, лучше понять их поведение, исследовать их характеристики, в том числе погрешности измерений, а также передачу и обработку результатов измерений. Если пренебречь воздействием влияющих величин и полагать, что в данный момент времени на вход системы поступает единственная измеряемая величина xe, которой соответствует одна выходная величина xa, то такую систему можно описать статической характеристикой вида xa = f(xe). Для более общего анализа необходимо учитывать изменение этих величин во времени:
xa(t) = f[xe(t)].
Измеряемая величина лишь в редких случаях сохраняет постоянное значение в процессе измерений. Часто постоянство измеряемой величины является кажущимся, так как она наблюдается на фоне помех, которые приходится оценивать, чтобы исключить из результата измерения. Примером сказанного может служить измерение длины l металлического бруска, которая постоянна лишь при неизменной температуре окружающей среды.
Из последнего примера можно сделать вывод еще об одном важном ограничении при системном рассмотрении средств измерений: наряду с входными величинами нельзя не учитывать влияния окружающей среды, проявляющегося в виде воздействий влияющих величин, в том числе помех и шумов. Оценивание и ограничение влияния подобных мешающих воздействий — важнейшая задача системотехники.
В заключение можно выделить следующие общие положения, которыми надо руководствоваться при рассмотрении средств измерений в качестве информационной измерительной системы:
Ø важнейшими видами взаимодействия информационной измерительной системы с окружающей средой являются отбор информации, определение значений измеряемых величин и выдача их в виде выходной информации;
Ø существует причинно-следственная связь между входной и выходной информацией в направлении от входа к выходу, т.е. xe → xa;
Ø желательно, чтобы информационная измерительная система как можно меньше влияла на входную (измеряемую) величину;
Ø воздействие помех и вызываемые ими погрешности играют при этом второстепенную роль;
Ø в автономных измерительных устройствах материальные связи с окружающей средой нередко отсутствуют, а наличие или отсутствие энергетических связей не имеет существенного значения для рассмотрения (их наличие обычно вызывает появление дополнительных шумов и помех);
Ø для информационной измерительной системы весьма желательна не имеющая запаздывания линейная передаточная характеристика вида xa = Kpxe в любой момент времени, где Kp — коэффициент передачи;
Ø передаточная характеристика информационной измерительной системы должна быть воспроизводимой и инвариантной относительно времени, т.е. зависимость между входной и выходной величинами не должна изменяться со временем.
Измерительная информация
Существует ряд определений понятия информации, что свидетельствует об их неудовлетворительности. Поэтому для уяснения этого понятия необходимо рассмотреть некоторые важнейшие свойства информации, исключая такие ее человеческие аспекты, как семантика (значимость информации для людей) и прагматика (воздействие информации на людей). Значимость измерительной информации следует рассматривать с точки зрения ее получения, т.е. выбора одного или нескольких значений измеряемой величины из имеющегося множества, что связано со статистическим подходом.
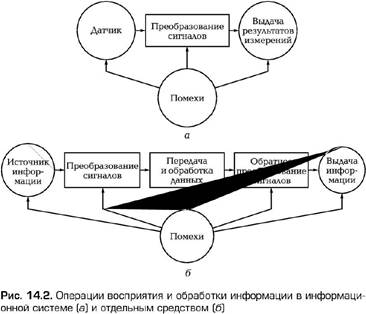
Каждое средство измерений обеспечивает выделение и восприятие информации, что схематично отражено на (рис. 14.2 а), в сравнении с передачей и обработкой сигналов в информационной системе, схематично показанных на (рис. 14.2 б). Элементы этих схем представляют собой операции над информацией (сигналами), а не физические устройства.
Один из подходов к толкованию информации в измерительной технике основан на положениях теории вероятностей, включающих оценку вероятности измеренного значения. Если до начала измерений известно, что вероятность pV того, что значение искомой величины заключено в определенном интервале, весьма мала, то эту вероятность оценивают путем измерений. Вероятность pV определенного значения измеряемой величины тем меньше, чем больше число уровней квантования или различимых ступеней значений этой величины. Если полагать, что каждое значение измеряемой величины в пределах измерений может появиться с одной и той же вероятностью
pV = 1/m.
то вероятность появления любого возможного значения этой величины составит
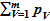 = 1.
= 1.
Число различимых ступенейm измеряемой величины зависит от погрешности средства измерений. Поясним сказанное на примере шкалы гипотетического измерительного прибора, изображенной на (рис. 14.3 а). Абсолютная погрешность, с которой выполняется каждое измерение, составляет e = ±1 (деление шкалы), а относительная погрешность e° = ±0,05 или ±5%. Иначе говоря, измеренное значение может быть заключено, к примеру, между 1 и 3, если указатель показывает цифру 2. В начале шкалы слева от 0 может быть деление — 1. Число m делений (различимых значений) в данном случае составляет
M = 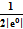 + 1 = 11.
+ 1 = 11.
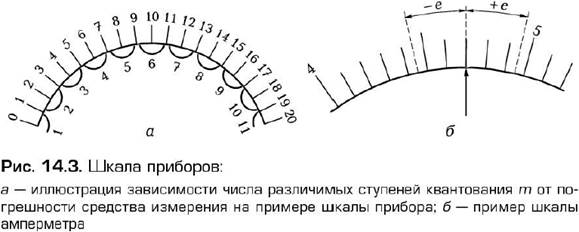
Рассмотрим другой пример — измеритель тока с пределами от 0 до 10A с «ценой» деления (шагом) шкалы 0,1A. И хотя число делений на шкале равно 100 вследствие того, что e° = 0,025, оказывается, что m = 21, т.е. различимы значения 0, 0,5, 1,0…, 9,5, 10 при абсолютной погрешности e = ±0,25A. Вероятность появления любого из перечисленных различимых значений составит pV = 21‒1 = 0,0476, или pV = 4,76%. Если желательно знать измеренное значение на ±0,5A точнее, то при упомянутой выше вероятности это исключено, что и иллюстрирует (рис. 14.3 б), где показана часть шкалы измерителя тока с положением стрелки против значения 4,7A. При этом значение 4,5A характеризуется 100%-й вероятностью, а значение 5A исключается, так как последнее лежит за границами погрешности. Если хотят узнать силу тока точнее на ±0,1A, то вероятность значения 4,7A составит 20%; при этом возможны значения 4,5 и 4,6A, а также 4,8 и 4,9A, лежащие в пределах границ погрешности ±e. Вероятность появления определенного значения изменяется в рассмотренном случае от 4,76 до 100%.
Измерения можно трактовать (в статистическом смысле) как поиск информации с уменьшением неопределенности и увеличением вероятности.
