Глоссарий (толковый словарь терминов)

Глоссарий по цифровой обработке сигналов [Доп.11]

ПРЕОБРАЗОВАНИЯ СИГНАЛОВ

Сигнал (Signal) – то, что математики обычно называют функцией. Под сигналом можно понимать какое-то упорядоченное множество чисел, несущих информацию о некотором процессе. Обычно описывается двумя (одномерный сигнал), тремя (двумерный сигнал) или более (многомерный сигнал) параметрами. Представляется в виде конечной или бесконечной совокупности точек. Одним из параметров для всех типов сигналов является значение уровня сигнала (его энергии) во всех точках. В качестве других параметров обычно выступают время (одномерный сигнал), пространственные координаты (двумерный и многомерные сигналы). Значения всех параметров могут быть непрерывными или дискретными. Таким образом, для каждой размерности можно различать 2L сигналов, где L- размерность сигнала. Например, в одномерном случае существуют сигналы, непрерывные по времени и уровню, дискретные по времени и уровню, дискретные по времени и непрерывные по уровню, непрерывные по времени и дискретные по уровню. Преобразование непрерывного по времени и уровню сигнала в дискретный по времени и уровню сигнал называется аналого-цифровым преобразованием (АЦП), обратное преобразование - ЦАП. Так как эти вопросы выходят за рамки глоссария, в дальнейшем все сигналы считаются дискретными по времени и уровню, то есть цифровыми.

Преобразования сигналов (Signal Transform) – понятие, вообще говоря, очень широкое и включает в себя любую операцию, производимую над сигналом. В рамках словаря под преобразованием мы будем понимать лишь обобщенное преобразование Фурье (см. Преобразование Фурье). Преобразование переводит сигнал из одной области представления в другую. Прямое преобразование 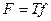переводит сигнал из временной (пространственной) области в область спектра, которая еще называется трансформантой. Обратное преобразование 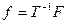переводит сигнал из области трансформанты во временную (пространственную) область.

Преобразования сигналов используются для разных целей: его сжатия, анализа и т.д. Анализ заключается в выполнении каких-нибудь действий над сигналом и формулировке выводов на основе полученных данных.

Спектр (Spectr) – представление сигнала в виде конечной или бесконечной суммы некоторых элементарных сигналов, умноженных на некоторые числа. В качестве элементарных сигналов обычно выступают ортогональные функции, такие как Фурье, Уолша, Хаара, Адамара, Хартли, вейвлеты и т.д. Поэтому говорят о спектре Фурье, Уолша и т.д. Числа, на которые умножаются элементарные сигналы называются спектральными коэффициентами (коэффициентами трансформанты). Часто просто говорят о коэффициентах Фурье, Уолша и т.д.

Базис (Basis) – совокупность векторов пространства 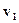обладающих следующим свойством: любой вектор пространства может быть представлен единственным образом как их линейная комбинация 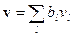. Число базисных векторов равно размерности пространства. Аналогично и последовательность функций 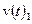является базисом функционального пространства, если любая функция из этого пространства может быть

представлена единственным образом как 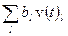. Числа 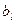называются коэффициентами разложения.

Биортогональный базис (дуальный базис). Дуальный базис 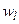биортогонален исходному базису: 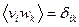. Тогда коэффициенты разложения 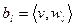(находятся на этапе анализа) и 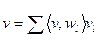(вычисляется при синтезе).

Ортогональный базис – частный случай биортогонального базиса, когда базисные векторы биортогональны самим себе. В этом случае дуальный базис идентичен исходному базису.

Линейное преобразование (Linear transform) – преобразование, удовлетворяющее условию: преобразование суммы сигналов равно сумме преобразований каждого сигнала. Большинство рассматриваемых в ЦОС преобразований – линейно.

Унитарное преобразование (Unitary transform)– преобразование, сохраняющее норму сигнала. Вещественное унитарное преобразование называется ортогональным. Его базисные функции ортогональны между собой. Важным свойством ортогонального преобразования является простая формула вычисления обратного преобразования. Все упомянутые выше преобразования являются унитарными.

Преобразование Фурье – (Fourier transform).

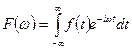- непрерывное.

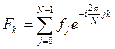- дискретное.

Оконное (Short-Time) преобразование Фурье (STFT) - (ОПФ) - определяется как преобразование Фурье сигнала, умноженного на некоторую взвешивающую функцию (окно). Так как окно локализовано по времени, ОПФ применяется для получения частотно-временного представления сигнала. В настоящее время предложено большое число различных окон: прямоугольное, треугольное, Ханна, Хэмминга и др. Простейшим из них является прямоугольное, соответствующее случаю умножения сигнала на константу. Так как преобразованием Фурье прямоугольника служит осциллирующая sinc-функция, то применять такое окно не рекомендуется.

Преобразование Габора – оконное преобразование Фурье с окном .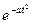

Преобразование Карунена-Лоэва (ПКЛ) – базисные функции естьсобственные векторы ковариационной матрицы входного сигнала. Является оптимальным по критерию достижения декорреляции входного сигнала. Энергия входного сигнала максимально перераспределяется в коэффициентах ПКЛ. Гарантируется, что процентное содержание энергии входного сигнала в данном количестве наибольших коэффициентов будет не меньше, чем в том же числе коэффициентов любого другого преобразования. Вычислительно трудоемко, кроме того, для вычисления обратного преобразования декодеру надо передавать базисные функции, найденные кодером. Поэтому, на практике не применяется. Все остальные преобразования часто сравниваются с ПКЛ.

Дискретное преобразование Хаара (Haar transform) – разложениесигналов по ортонормальному базису вейвлетов Хаара.

Дискретное косинусное преобразование - ДКП (Discrete cosine transform - DCT). Существует четыре основных типа ДКП: Определяется и дискретное синусное преобразование (косинусы заменяются на синусы). Оба преобразования являются ортогональными.

Перекрывающееся ортогональное преобразование (ПОП) (Lapped Orthogonal Transform - LOT). При ПОП почти отсутствуют эффекты блочности, присущие ДКП.

Обобщенное перекрывающееся ортогональное преобразование (GenLOT) – результат ПОП умножается на дополнительные матрицы. И ДКП, и ПОП являются частными случаями этого преобразования.

Преобразование Хартли (Hartley) – одно альтернатив ДПФ, использует вещественные функции. Одно время рассматривалось как панацея ЦОС, но потом оказалось в тени вейвлет-преобразования.

Свертка (Convolution). Сверткой двух векторов 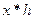называется вектор, n -й элемент которого равен .

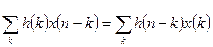ФИЛЬТРЫ

Фильтр (Filter) – линейная стационарная система, то есть свойства фильтра не зависят от времени. Независимость свойств фильтра от времени означает, что задержка входа приводит к такой же задержке выхода. К основным характеристикам фильтров относятся импульсная характеристика 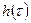, передаточная характеристика 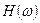, частотная характеристика, порядок фильтра.

Каузальный (Causal) фильтр - реакция фильтра не может предшествовать приложенному воздействию. Система каузальна, если выходной сигнал зависит от входного сигнала только в моменты времени до момента наблюдения.

Стабильный фильтр (физически реализуемый) – сумма коэффициентов импульсной характеристики небесконечна. У каузального и стабильного фильтра все нули передаточной функции находятся внутри единичного круга.

M -полосный фильтр (фильтр Найквиста) - один из наиболее частоиспользующихся типов фильтров. Находит применение при обработке сигналов, в связи, в многоскоростных системах, при построении сигма-дельта АЦП, фильтров децимации и интерполяции.

Всепропускающий (Allpass) фильтр – фильтр, частотная характеристика которого вещественна, а ее модуль равен 1.

Фильтр Баттерворта (максимально плоский фильтр) –в полосе пропускания практически нет колебаний. Это является преимуществом для многих приложений, где требуется постоянство коэффициента ослабления фильтра для всех частот полосы пропускания. Недостатком такого фильтра является невысокая крутизна полосы перехода.

Дополнительные по мощности (Power Complementary) фильтры - Примерами могут служить фильтры параунитарного банка фильтров.

Квадратурно-зеркальный фильтр – КЗФ (Quadrature Mirror Filter - QMF) – пара фильтров ВЧ и НЧ характеристики которых симметричны относительно средней частоты. Эта частота называется квадратурной, отсюда и название фильтров. КЗФ могут быть как с КИХ, так и с БИХ. Банк фильтров КЗФ может быть М-полосным.

БАНКИ ФИЛЬТРОВ

Банк фильтров (Filter Bank) – совокупность фильтров и следующих за ними дециматоров или следующих перед ними интерполяторов. Под дециматором понимается устройство, осуществляющее децимацию (прореживание) сигнала. Интерполятор выполняет интерполяцию сигнала. Банки фильтров бывают равномерные и неравномерные, ортогональные, биортогональные, двухканальные и многоканальные и т.д. Каждый фильтр банка фильтров образует канал. Поэтому говорят об M -канальном банке фильтров. Сигнал в канале назыается субполосой. Отсюда название субполосная фильтрация (субполосное кодирование). В случае если число каналов равно коэффициенту децимации (интерполяции) говорят о максимально (критически) децимированном банке фильтров. Быстрый алгоритм вычисления вейвлет-преобразования строится именно на основе таких банков фильтров. Равномерный банк фильтров – децимация в каждом канале одинаковая. В противном случае – неравномерный банк фильтров. Частный случай неравномерного банка фильтров - древовидный банк фильтров.

Децимация (прореживание) (Decimation) –операция, заключающаяся в выбрасывании отсчетов, чей порядковый номер кратен определенному числу. Например, при децимации в два раза выбрасывается каждый второй отсчет, при прореживании в три раза – каждый третий и т.д. Спектр выходного сигнала при операции децимации содержит M копий «расширенного» в M раз спектра входного сигнала. Если сигнал не ограничен полосой частот, то происходит наложение спектров копий, то есть элайзинг. Поэтому в банке фильтров перед децимацией выполняется НЧ фильтрация. Совокупность фильтра и дециматора называется фильтром-дециматором.

Интерполяция (Interpolation) – операция, заключающаяся во встраивании между отсчетами, чей порядковый номер кратен определенному числу, некоторой константы (обычно нуля).