Описание установки и метода исследования

Схема установки, состоящей из соленоида (С) и четырех катушек (K₁, K₂, K_3, K₄), представлена на рис. 8.3.

Соленоид представляет полую трубу, изготовленную из диэлек­три­чес­кого материала, на которую намотана медная проволока виток к витку в один слой. Диаметр соленоида 111 мм, длина 1 м, количество витков N= 1000. Все катушки изготовлены подобно соленоиду, т.е. намотаны на диэлектрические каркасы медной проволокой в один слой. Параметры катушек приведены в табл. 8.1 . Катушки K₁ , K₂, K₃, закрепленные на

Таблица 8.1

Номер катушки	Диаметр d, мм	Число витков
K1 K2 K3 K4	39,3 60,4 85,0

круглой диэлектрической пластине, помещаются внутри соленоида в центральной его части. Концы катушек выведены из соленоида наружу. Катушка K₄ жестко закреплена. Она охватывает соленоид снаружи. Ток, текущий по соленоиду, создает магнитное поле, пронизывающее контуры всех катушек.

Выведем формулу для определения теоретического значения ЭДС индукции (e_iТ) в любой катушке, находящейся в поле бесконечного соленоида. Пусть по соленоиду течет ток I, меняющийся по гармоничес-кому закону

I = I₀ сos w t.

(Если ток в соленоиде не будет меняться, то ЭДС индукции в неподвижных катушках не возникает, так как магнитный поток, пронизывающий катушку, не зависит от времени). Индукция магнитного поля внутри соленоида без сердечника в любой момент времени определяется по формуле

B = m₀n I.

Магнитный поток, пронизывающий один виток катушки, находящейся внутри соленоида, определяется выражением

Ф = B S = m₀ n I S,

где S- площадь одного витка катушки. Полный магнитный поток, пронизывающий катушку, содержащую N витков,

Y = Ф N = m₀n I S N

или

,(8.9)

где d- диаметр катушки; I₀- амплитудное значение тока; w- циклическая частота.

ЭДС индукции, возникающая в катушке, определяется выражением

. (8.10)

Выражение (8.10) определяет теоретическое значение ЭДС индукции, возникающей в любой катушке, находящейся в поле бесконечного соленоида, по которому течет ток, меняющийся по гармоническому закону.

Амплитудное значение возникающей ЭДС индукции

. (8.11)

Если в выражении (8.11) амплитудное значение тока заменить действующим значением I_Д, то полученное выражение будет определять действующее значение возникающей ЭДС

. (8.12)

Таким образом, задав параметры катушки, соленоида и тока, текущего по нему, можно определить теоретическое значение действу-ющей ЭДС, используя выражение (8.12).

Порядок выполнения работы

1. Оценить погрешность, которую дает соленоид конечных размеров, при определении вектора 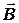по сравнению с бесконечным соленоидом.

Поле бесконечного соленоида однородно. В данной работе все теоретические формулы базируются на предположении, что магнитное поле создается бесконечно длинным соленоидом, т.е. индукция магнитного поля определяется выражением (8.5). Рабочий же соленоид имеет конечные размеры, следовательно, реальная индукция магнитного поля будет другая. Поэтому между теоретическими и экспериментальными результатами дляe_iбудет некоторое расхождение, оценить которое можно следующим образом

. (8.13)

Подставив в выражение (8.13) формулы (8.5) и (8.6), получим

. (8.14)

Зависимость между e_i и Влинейная, поэтому расхождение при определении теоретического и экспериментального значений ЭДС не должно превышать расхождения для В.

По известным параметрам l и d (см. рис. 8.1) определим соs a₁ и сosa₂ не менее чем для двух точек, находящихся на оси соленоида в центральной его части.

Используя выражение (8.14), оценим расхождение для В в этих точках.

2. Теоретически и экспериментально определить ЭДС индукции в катушках.

2.1. Собрать схему (рис.8.4).

2.2. Подать напряжение с блока питания на соленоид. Частота подаваемого напряжения определяется по указанию преподавателя. По миллиамперметру определить величину тока I_д .

Таблица 8.2   ЭДС K1 K2 K3 K4 eiэ eiТ

2.3. Поочередно подключая милливольтметр к выводам катушек, определить ЭДС, возникающую в них. Результаты занести в табл. 8.2 в строку e_iэ.

2.4. Используя выра­же­ние (8.12), вычислить теоре­ти­чес­кое значение e_iТ в каж­дой ка­­тушке при I_диw, оп­ре­де­лен­­ных в п.2.

2.5. Оценить расхож­де­ние, полученное при тео­ре­ти­чес­ком и экспериментальном определении ЭДС. Сравнить его с тем, которое было получено в п. 1, и сделать вывод.

3. Определить зависимость e_i = f (s), где s -площадь катушки.

3.1. Используя экспериментальные данные, полученные в п. 2, вычислить ЭДС, возникающую в одном витке каждой катушки.

3.2. Построить график зависимости e_i = f (s).

4. Определить сдвиг фаз между током, текущим по соленоиду, и ЭДС индукции, возникающей в любой из катушек.

Выше было показано, что, если сила тока в соленоиде меняется по закону I = I₀ сos w t, то

.

Это означает, что между током в соленоиде и ЭДС индукции в катушке существует сдвиг фаз. Для определения этого сдвига фаз воспользуемся осциллографом. Собрать схему (рис. 8.5). По виду фигуры, полученной на осциллографе, определим сдвиг фаз между током и ЭДС индукции.

5. Экспериментально сравнить коэффициенты взаимоиндукции L₁₂ и L₂₁.

5.1. Пропустить ток I = 0,5А через катушку K₁. Измерить ЭДС, возникающую в катушке K₃.

5.2. Пропустить такой же ток через катушку K₃. Измерить ЭДС, возникающую в катушке K₁. Сравнить полученные результаты и сделать вывод относительно L₁₂ и L₂₁.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем заключается явление электромагнитной индукции?

2. Что такое магнитный поток и как он вычисляется?

3. Что называется потокосцеплением?

4. Как определяется индукция магнитного поля для конечного и бесконечного соленоидов?

5. Что такое коэффициент взаимоиндукции?

6. Вывести формулу для ЭДС катушки, находящейся внутри бесконечного соленоида, по которому течет ток.

7. Что называется действующим значением тока и напряжения, и как они связаны с амплитудными значениями?

ЛАБОРАТОРНАЯ РАБОТА № 9