Каноническое распределение

КВАНТОВАЯ СТАТИСТИЧЕСКАЯ ФИЗИКА

Квантовая статистическая физика изучает системы из большого числа частиц, подчиняющихся законам квантовой механики:

электронный газ металла;

электроны и дырки в полупроводнике;

электромагнитное тепловое излучение в полости;

фононы в кристалле;

газ атомов при низкой температуре.

Учитываются квантовые свойства:

дискретность спектра энергии пространственно ограниченной

системы;

вырождение состояний по энергии;

тождественность микрочастиц;

принцип запрета Паули для фермионов.

Рассматриваются системы из множества частиц одинаковой природы, образующих идеальный газ:

объем, занятый системой, гораздо больше объема частиц;

частицы двигаются независимо друг от друга;

частицы не взаимодействуют между собой на расстоянии.

Физические свойства многочастичной системы определяются ее энергетическим спектром и распределением частиц по уровням энергии.

Плотность состояний

Энергетический спектр системы зависит от природы частиц и области пространства, занятой частицами. Чем больше объем пространства, тем меньше расстояние между уровнями энергии. При макроскопическом объеме системы ее спектр квазинепрерывный. Энергетический спектр характеризуется плотностью состояний – числом состояний в единичном интервале энергии

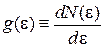. (3.3)

Число состояний с энергией в интервале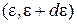

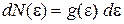(3.3а)

получим, используя объем фазового пространства системы и объем, занимаемый одним состоянием, с учетом вырождения состояний по энергии.

Число частиц в интервале энергии 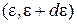равно произведению числа состояний 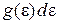на среднее число частиц 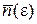в одном состоянии

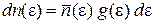. (3.10)

Кратность вырождения. Одним из квантовых чисел частицы является проекция спина S, число разных проекций 2S + 1. При отсутствии магнитного поля эти состояния имеют одинаковую энергию, тогда кратность вырождения

.

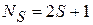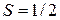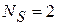Для электрона и . Для фотонного газа 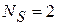, несмотря на спин 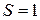. Теория относительности запрещает для фотона, движущегося со скоростью света, направление спина перпендикулярное к скорости, тогда остаются проекции по- и против скорости.

Плотность состояний. Условие квантования Бора–Зоммерфельда дает наименьший объем фазового пространства одномерного движения, занимаемый одним состоянием:

.

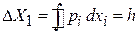Бесспиновое состояние с одной степенью свободы занимает фазовый объем, равный постоянной Планкаh. Состояние частицы с f степенями свободы занимает объем 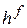, тогда в элементе фазового объема 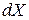находится число состояний

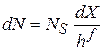. (3.4)

Из (3.3) 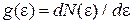получаем плотность состояний

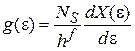, (3.5)

где 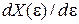– приращение объема фазового пространства при увеличении энергии на единицу. Величина

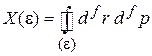
является объемом фазового пространства, ограниченным гиперповерхностью с полной энергией ε. Для вычисления 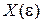используем связь полной энергии частицы с импульсами и координатами.

Если отсутствует внешняя сила, действующая на частицу, то ее энергия ε не зависит от положения частицы в объеме 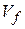, занятым системой. Интегрируем по координатам, и получаем

,

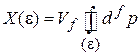тогда

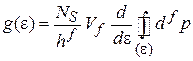. (3.5а)

Для вычисления объема импульсного пространства 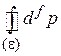, ограниченного гиперповерхностью с полной энергией ε, требуется знать соотношение между энергией и импульсом частицы.

Квадратичная зависимость энергии от импульса для f-мерного движения

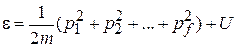, (3.6)

где U не зависит от координат 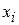. Согласно (3.6) все координаты импульсного пространства 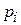, где 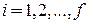, равноправные. Состояние с полной энергией e находится в импульсном пространстве на f-мерной сфере радиусом

.

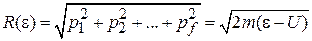Объем f-мерного шара находим из (П.2.1)

.

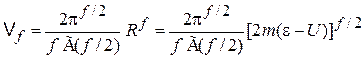Подставляем в (3.5а)

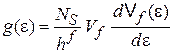
и получаем

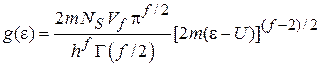. (3.7)

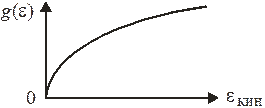
Плотность состояний определяется кинетической энергией частицы .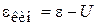

Трехмерный газ. При 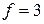из (3.7) находим

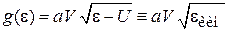, (3.8)

где

.

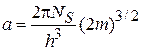В интервале энергии 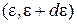находится число состояний

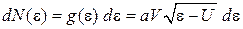. (3.9)

Для классического идеального трехмерного газа 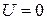, 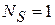и из (3.8) получаем известную ранее формулу

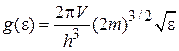. (3.8а)

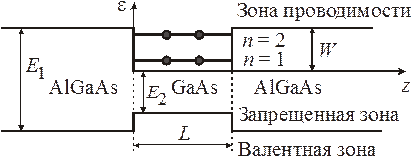
Двухмерный газ в слое. Полупроводниковая гетероструктура содержит слой 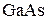толщиной 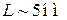с запрещенной зоной шириной 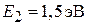. Снаружи находятся слои 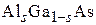с запрещенной зоной 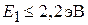. В зоне проводимости 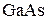образуется потенциальная яма глубиной до 0,4 эВ с энергетическими уровнями, или зонами 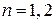. Электроны этих зон движутся свободно в плоскости 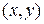слоя 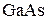, образуя двухмерный газ. Ось z перпендикулярна слою.

Энергию частицы в слое отсчитываем от дна потенциальной ямы

,

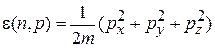где 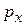и 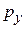– любые, 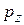– квантуется. Для бесконечно глубокой ямы шириной L волновая функция равна нулю на стенках слоя. В яме укладывается целое число n полуволн де Бройля

.

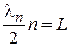В результате квантуются проекция импульса на ось z и энергия частицы

,

,

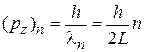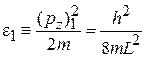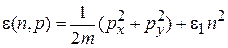. (П.8.3)

Сравниваем (П.8.3) с (3.6)

,

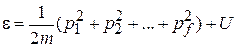находим

, .

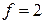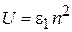Используем (3.7)

,

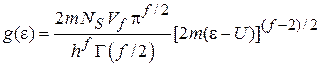учитываем 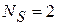, 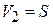и получаем плотность состояний на уровне энергии n

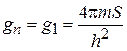. (П.8.4)

Уровень, который может занять частица, называется активизированным. В двухмерной системе плотность состояний активизированного уровня не зависит от его энергии. Число уровней 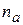, активизированных до энергии 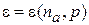, находим из (П.8.3)

.

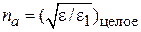В плотность состояний частиц с энергией в интервале от 0 до ε вносят вклад все активизированные уровни. В результате плотность состояний электронного газа с энергией ε

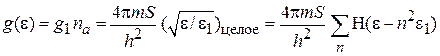, (П.8.4а)

где Н – функция Хевисайда. На рисунке пунктирная кривая – 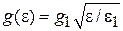. С ростом энергии плотность состояний увеличивается скачком на величину g₁ каждый раз, когда энергия частицы достигает разрешенного уровня, и частицы начинают его заполнять, увеличивая продольный импульс. В точке перехода на очередной уровень продольный импульс 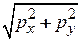обращается в нуль, поперечный импульс 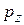скачком увеличивается на .

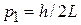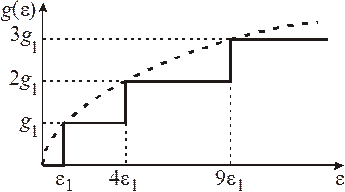
Плотность состояний в слое

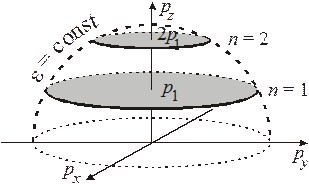
Активизированные уровни ( ).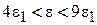

Тонирована область импульсного пространства, занятого частицами.

Одномерный газ в нити. Ось z направляем вдоль нити. Поперечный импульс частицы квантуется, импульс 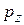продольного движения может быть любым. Энергия

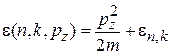, (П.8.5)

где 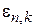– уровни энергии поперечного движения с квантовыми числами 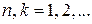Сравниваем (П.8.5) с (3.6)

,

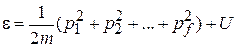находим

, .

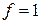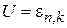Используем (3.7)

,

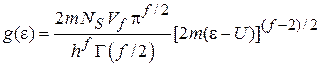учитываем 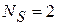, , 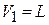и получаем плотность состояний активизированного уровня

.

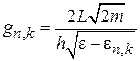В плотности состояний с энергией от 0 до ε суммируются вклады всех активизированных уровней. Для энергии ε получаем

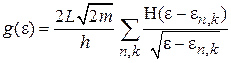. (П.8.6)

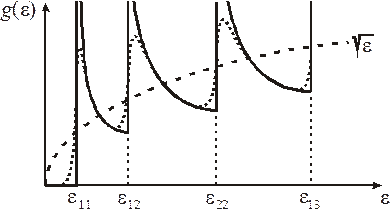
Неоднородность поперечного сечения нити приводит к уширению уровней энергии и к конечным значениям плотности состояний при 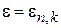, как показано точечной кривой на рисунке.

Нульмерный газ в квантовой точке(КТ). КТ является полупроводниковым нанокристаллом с поперечником L ~ (1 – 100) нм во внешней среде с близким значением постоянной решетки и бóльшей шириной запрещенной зоны. КТ является потенциальной ямой с энергетическим спектром 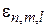, с числом уровней ~ (2 – 3). Расстояние между уровнями

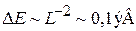
относительно велико за счет малости L. При нормальной температуре тепловая энергия относительно мала

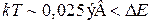
и электроны занимают низшие состояния. Это обеспечивает температурную стабильность КТ. Расстояние между КТ ~ 100 нм. Электроемкость КТ мала

,

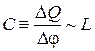поэтому добавление электрона 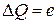существенно изменяет потенциал 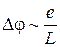и коэффициент прохождения через КТ. Второй электрон не может попасть в КТ благодаря кулоновскому отталкиванию, возникает кулоновская блокада. Электрон может двигаться через КТ за счет туннельного эффекта.

При увеличении энергии электрона, когда она переходит через очередной уровень 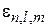, число состояний N(e) возрастает на величину, равную кратности вырождения 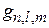уровня, тогда

.

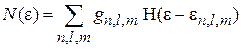Используя (3.3)

,

,

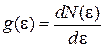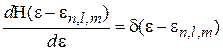находим плотность состояний в КТ:

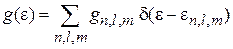. (П.8.7)

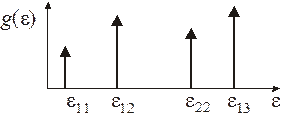
Неоднородность микроскопического поперечного сечения КТ приводит к уширению уровней энергии и к конечным значениям плотности состояний при .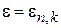

Фотонный газ в полости. Имеется замкнутая полость объемом V, наполненная множеством квантов электромагнитных волн, созданных тепловым движением микрочастиц стенок полости.

Теория относительности допускает у кванта со спином 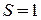, движущегося со скоростью света, две проекции спина – по и против скорости. Поэтому электромагнитная волна поперечная, имеет две независимые поляризации,

, .

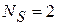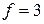Излучение в полости распределено равномерно по ее объему V и по направлениям движения в пределах полного телесного угла 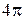. Элемент фазового объема кванта в сферических координатах по импульсу

.

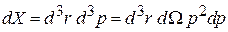Интегрируем по объему полости и по направлениям вектора импульса. Получаем фазовый объем, занятый фотоном с модулем импульса в интервале :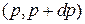

.

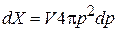Модуль импульса выражаем через энергию, используя закон дисперсии релятивистской частицы:

,

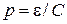получаем фазовый объем, занятый фотоном с энергией в интервале :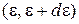

.

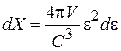Находим число состояний (3.4)

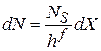
в интервале энергии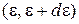

,

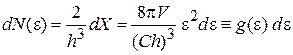где плотность состояний

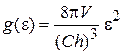. (П.8.9)

Замена 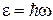дает

,

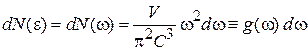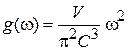. (П.8.9а)

Фононный газ атомного кристалла в модели Дебая. Фононы – кванты упругих волн в кристалле. Существует три типа поляризации акустической волны в кристалле – два поперечных и один продольный. Волне в кристалле с частотой ω соответствует квант энергии

.

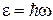Связь импульса фонона с энергией зависит от типа кристалла и интервала частот. Для низких частот используется модельДебая, описывающая акустическую ветвь спектра упругих колебаний, где импульс фонона линейно зависит от частоты аналогично импульсу фотона

,

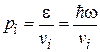где i = 1, 2, 3 – тип поляризации волны; 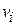– скорость волны. Для продольных волн 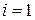аналогично фотонному газу находим

, ,

.

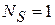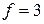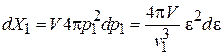Для числа состояний и плотности состояний получаем

,

.

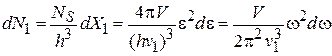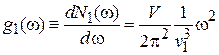Аналогичные выражения имеем для поперечных волн 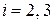. Состояния независимые, поэтому результирующая плотность состояний

.

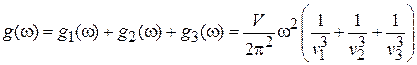Вводим среднюю скорость звука v

,

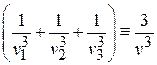и получаем

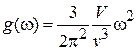, (П.8.10)

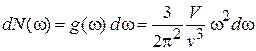. (П.8.11)

Каноническое распределение