Середнє значення випадкової величини

При вивченні руху молекул ми користувалися середніми значеннями фізичних величин:

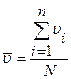– середня швидкість

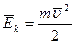– середня кінетична енергія

Це зручно, оскільки для описання систем, які включають в себе велике число молекул або інших частинок, немає ані можливості, ані необхідності використовувати величини, які відносяться до кожної з молекул окремо. Більш того, саме використання середніх значень вищеназваних величин дозволило нам знайти закон-рівняння стану ідеального газу, який підтверджується на практиці. Отже, саме середні значення фізичних величин визначають стан системи багатьох частинок та являються її об’єктивними макроскопічними параметрами.

Виявляється, що середні значення фізичних величин тісно пов’язані з поняттям ймовірності. Але у зв’язку з цим закони молекулярної фізики не втрачають нічого у своїй точності і визначеності. Це пояснюється тим, що для всякої системи, яка знаходиться у незмінних зовнішніх умовах, фізичні величини, що описують її, також практично незмінні і дорівнюють своїм середнім значенням.

Нехай деяка випадкова величина а приймає ряд дискретних значень: 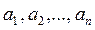. Середнє значення визначається рівністю:

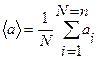(19)

Зваживши на те, що деякі значення a_i можуть бути рівними, цю суму можемо перегрупувати іншим способом. Такі однакові результати a_i можна спостерігати протягом різної кількості дослідів. Наприклад, значення a₁ ми отримали N₁ разів, a₂ – N₂, і т. д. При цьому:

N₁ + N₂ +…+N_k = N

Тому рівність (19) перепишемо

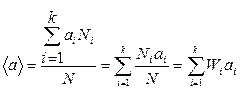
де 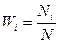- ймовірність того, що а приймає значення а_і.

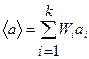Þ (20)

Таким чином, середнє значення 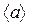випадкової величини а дорівнює сумі добутків окремих її значень a_i на відповідні ймовірності.

В математиці цю ж саму величину 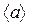називають математичним очікуванням випадкової величини.

Середнє значення будь-якої функції від а дорівнює:

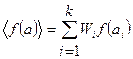(21)

Ми розглянули середнє значення дискретної випадкової величини. Коли ж випадкова фізична величина змінюється неперервно, то вираз (20) запишеться:

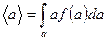(22)

де 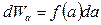– ймовірність існування значення фізичної величини в інтервалі від а до а+ da.

Наприклад, для швидкості

,

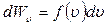і формула (22) набуває вигляду:

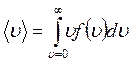(23)

Оскільки 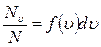, то у 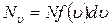випадках будуть спостерігатися значення швидкості від u до u + du, близькі до значення u, а сума таких результатів дорівнює :

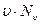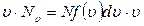
Проінтегрувавши останній вираз у межах від u = 0 до u = ¥ , отримаємо суму усіх можливих результатів:

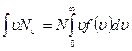
Розділивши цю суму швидкостей на число вимірювань N, отримаємо середнє значення, тобто:

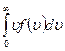(24)

В загального випадку, середнє значення будь-якої функції 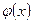можна знайти за формулою:

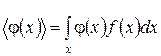(25)

Розглянемо деякі властивості середніх значень.

1) Нехай маємо дві різні функції від випадкової величини а: f(a) і j(a). Тоді середнє значення від суми дорівнює:

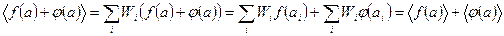(26)

2) Якщо С стала, то середнє значення від добутку:

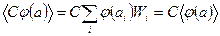(27)

3) Якщо f(a) функція а, а j(b) функція іншої випадкової величини b, тоді маємо:

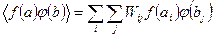(28)

Якщо змінні а і b описують 2 статистично незалежні системи, то ймовірність перемножується 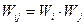і тоді отримуємо для середніх значень:

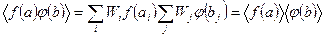(29)

Флуктуації

Використовуючи функції розподілу, можна визначити середні значення макроскопічних параметрів стану термодинамічної системи. Однак у будь-якій навіть рівноважній системі існують випадкові відхилення від цих середніх значень, які можна експериментально спостерігати при вимірюваннях термодинамічних параметрів стану системи. Зазначені відхилення від середніх значень називаються флуктуаціями. Вони виникають внаслідок хаотичного теплового руху частинок термодинамічної системи. Будемо розглядати тільки флуктуації в рівноважній системі, що відповідно називаються рівноважними флуктуаціями.

Флуктуація характеризує, як часто стан системи відхиляється від свого середнього значення. Нехай рівноважний стан системи характеризується деяким параметром а, середнє значення якого дорівнює 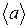. Тоді флуктуації цього параметра визначаються як відхилення його значення від середнього:

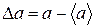(30)

Оскільки відхилення від середнього значення можуть бути абсолютно різними, то зручніше характеризувати їх також середньою величиною. Але тоді визначення (30) не годиться для цього, оскільки середнє значення від нього 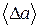дорівнює 0:

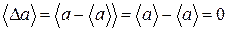(31)

Для кількісної оцінки величини флуктуацій можна використовувати середній квадрат відхилення параметра а від його середнього значення:

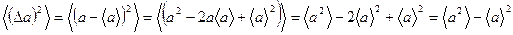(31)

Аналогічну формулу можна записати і для середнього квадрата флуктуацій 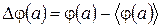будь-якої функції :

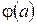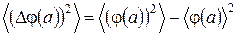(32)

Часто характеризують флуктуації так званою дисперсією. Математично вона визначається як середнє значення квадратів відхилення окремих значень a_i величини а від її середнього значення 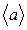і виражається за допомогою формули:

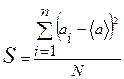(33)

де 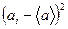– квадрат відхилення результату і-го вимірювання від середнього значення 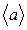випадкової величини а. Крім того,

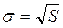(34)

де s – середньоквадратичне(стандартне) відхиленнярезультату і-го вимірювання від середнього значення.

З урахуванням формул (20) і (22), отримаємо такий вираз для середнього квадрата відхилення, тобто для дисперсії:

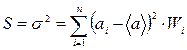(35) –для дискретних значень випадкової величини

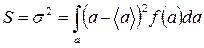(36) – для неперервної випадкової величини.