| | Свет представляет собой: | |
| | продольную электромагнитную волну, распространяющуюся в некотором светонесущем эфире; | |
| | поперечную электромагнитную волну, распространяющуюся в направлении перпендикулярном колебаниям векторов 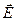 и и 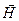 - напряженности электрического и магнитного полей; - напряженности электрического и магнитного полей; | 1 |
| | поперечную электромагнитную волну, распростроняющуюся в направлении, которое определяется вращением правого винта относительно векторов 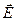 и и 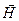 - напряженности электрического и магнитного полей. - напряженности электрического и магнитного полей. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Физиологическое, фотохимическое, фотоэлектрическое и др. действие света обусловлено: | |
| | колебаниями вектора 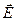 - напряженности электрического поля; - напряженности электрического поля; | 1 |
| | колебаниями вектора 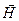 - напряженности магнитного поля; - напряженности магнитного поля; | |
| | колебаниями вектора 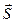 - вектора Умова-Пойтинга. - вектора Умова-Пойтинга. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Световым вектором называется: | |
| | вектор напряженности электрического поля 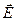 как составляющая электромагнитной волны; как составляющая электромагнитной волны; | 1 |
| | вектор напряженности магнитного поля 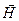 как составляющая электромагнитной волны; как составляющая электромагнитной волны; | |
| | вектор Умова-Пойтинга 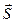 , определяющий плотность потока электромагнитной энергии. , определяющий плотность потока электромагнитной энергии. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Изменение во времени и пространстве проекции светового вектора на направление, вдоль которого он колеблется, описывается уравнением 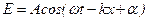 , где , где | |
| | k – волновое число; | 1 |
| | k – коэффициент перемещения световой волны; | |
| | k – фаза волны. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Интенсивностью света называется | |
| | модуль среднего по времени значения плотности потока энергии, переносимого световой волной; | 1 |
| | квадрат амплитуды светового вектора; | |
| | произведение амплитуды вектора напряженности магнитного поля на амплитуду вектора электрического поля как составляющих электромагнитной волны (ЕтхНт). | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Интенсивность волны прямопропорциональна: | |
| | квадрату амплитуды светового вектора; | 1 |
| | квадрату показателя преломления среды, в которой эта волна распространяется; | |
| | модулю значения среднего по времени вектора напряженности электрического поля. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Интенсивность света I меряется в: | |
| | Вт/м2; | 1 |
| | Вт/м; | |
| | В/м. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Лучом называется: | |
| | линия, вдоль которой распространяется световая энергия; | 1 |
| | направление распространения световой волны; | |
| | направление колебаний светового вектора. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Интерференцией называется: | |
| | перераспределение интенсивности световых колебаний в результате наложения когерентных монохроматических световых волн; | 1 |
| | возникновение темных и светлых полос на экране в результате наложения двух когерентных волн; | |
| | согласованное протекание двух или нескольких волновых процессов в пространстве, в результате которого наблюдается разложение световой волны в спектр. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Когерентными называются колебания: | |
| | у которых разность фаз не изменяется с течением времени; | 1 |
| | у которых амплитуды колебания равны; | |
| | которые имеют равную частоту колебаний. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Когерентностью называется: | |
| | согласованное протекание нескольких колебательных или волновых процессов; | 1 |
| | перераспределение интенсивности световых колебаний; | |
| | усиление одного колебания другим. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Время в течении которого случайное изменение фазы световой волны не превышает π называется: | |
| | временем когерентности; | 1 |
| | временем излучения; | |
| | волновым цугом. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Длиной когерентности называется: | |
| | расстояние, на которое перемещается волна за время когерентности; | 1 |
| | расстояние, на которое перемещается волна за период; | |
| | расстояние между двумя точками волны колеблющимися в одинаковой фазе. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Пусть tприб – время срабатывания прибора, tког – время когерентности. Тогда, если tприб>>tког: | |
| | прибор не зафиксирует интерференции, следовательно, волны не когерентны; | 1 |
| | прибор зафиксирует интерференцию, следовательно, волны когерентны; | |
| | сравнение этих величин не дает возможности судить о когерентности волн. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Время когерентности будет тем больше, чем: | |
| | интервал частот, представленных в волне уже; | 1 |
| | интервал частот, представленных в волне шире; | |
| | в волне представлено больше частот видимого диапазона. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Для наблюдения интерференционной картины необходимо, чтобы Δ – оптическая разность хода и lког – длина когерентности были связаны соотношением: | |
| | Δ<lког; | 1 |
| | Δ>lког; | |
| | Δ=lког. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Число интерференционных полос: | |
| | возрастает с уменьшением интервала длин волн, представленных в световой волне; | 1 |
| | уменьшается с уменьшением интервала длин волн, представленных в световой волне: | |
| | возрастает с увеличением интервала длин волн, представленных в световой волне. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Когерентность колебаний, которые совершаются в одной и той же точке пространства и определяется степенью монохроматичности волн называется: | |
| | временной когерентностью; | 1 |
| | пространственной когерентностью; | |
| | волновой когерентностью. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Разброс направлений вектора 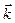 определяет: определяет: | |
| | пространственную когерентность; | 1 |
| | волновую когерентность; | |
| | временную когерентность. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Радиус когерентность определяет: | |
| | расстояние, в пределах которого будет наблюдаться интерференционная картина; | 1 |
| | максимальный радиус окружности с центром на источнике света, до которого достает излучение; | |
| | расстояние, которое проходит волна за время когерентности. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Когерентность, определяемая пространственными размерами источника, называется: | |
| | пространственной когерентностью; | 1 |
| | временной когерентностью; | |
| | когерентностью источника. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Оптической длиной пути называется: | |
| | произведение геометрического пути на показатель преломления среды, в которой распространяется свет; | 1 |
| | произведение геометрического пути на угол падения света; | |
| | расстояние, которое проходит световая волна за время t. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Оптическая разность хода Δ – это: | |
| | разность оптических длин, проходимых волнами путей; | 1 |
| | расстояние между интерференционными полосами; | |
| | расстояние между максимумами и минимумами интенсивности. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Условие интерференционного максимума имеет вид: | |
| | 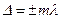 ; ; | 1 |
| | 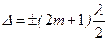 ; ; | |
| | 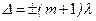 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Условие интерференционного минимума имеет вид: | |
| | 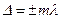 ; ; | |
| | 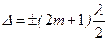 ; ; | 1 |
| | 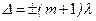 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Опыт Юнга заключается в: | |
| | получении интерференционной картины при прохождении света через две щели в непрозрачном экране; | 1 |
| | получении интерференционной картины при падении света на тонкую пленку; | |
| | получении интерференционной картины при прохождении света через систему: «тонкая пластинка + плосковыпуклая линза». | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В опыте Юнга положение интерференционных максимумов определяется формулой 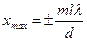 , где m – это: , где m – это: | |
| | порядок максимума; | 1 |
| | длина волны излучения; | |
| | масса фотона. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В опыте Юнга положение интерференционных минимумов определяется формулой 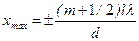 , где l – это: , где l – это: | |
| | расстояние от отверстий до экрана; | 1 |
| | расстояние между отверстиями; | |
| | длина волны излучения. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Расстояние между двумя ближайшими максимумами или минимумами называется: | |
| | шириной интерференционной полосы; | 1 |
| | длиной интерференционной полосы; | |
| | длиной когерентности. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Разность хода при падении света на плоскопараллельную пластину определяется соотношением: | |
| | 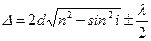 ; ; | 1 |
| | 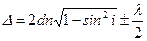 ; ; | |
| | 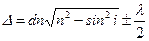 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Условие интерференционного максимума при падении света на тонкую пленку в отраженном свете имеет вид (пленку считать оптически более плотной): | |
| | 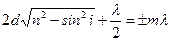 ; ; | 1 |
| | 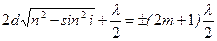 ; ; | |
| | 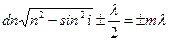 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Условие интерференционного минимума при падении света на тонкую пленку в проходящем свете имеет вид (пленку считать оптически более плотной): | |
| | 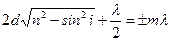 ; ; | 1 |
| | 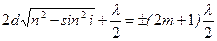 ; ; | |
| | 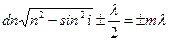 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Полосами равной толщины называются: | |
| | интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами; | 1 |
| | интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, пи падении света на пластину переменной толщины (клин); | |
| | интерференционные полосы, возникающие при падении света на два скрещенных под углом ≈180о зеркала. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Полосами равного наклона называются: | |
| | интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами; | |
| | интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, пи падении света на пластину переменной толщины (клин); | 1 |
| | интерференционные полосы, возникающие при падении света на два скрещенных под углом ≈180о зеркала. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Кольца Ньютона являются классическим примером: | |
| | полос равной толщины; | 1 |
| | полос равного наклона; | |
| | полос равного взаимодействия. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В отраженном свете радиус светлого кольца Ньютона определяется по формуле: | |
| | 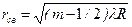 ; ; | 1 |
| | 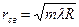 ; ; | |
| | 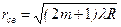 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В проходящем свете радиус темного кольца Ньютона определяется по формуле: | |
| | 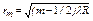 ; ; | 1 |
| | 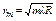 ; ; | |
| | 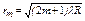 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В формуле разности хода света в плоскопараллельной пластине 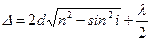 слагаемое « слагаемое « 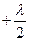 » определяет: » определяет: | |
| | потерю полуволны и изменение ее фазы при отражении от более плотной среды; | 1 |
| | потерю полуволны в результате дискретного (прерывистого) излучения атомами; | |
| | это слагаемое получается в результате геометрического построения оптической разности хода. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В формуле 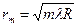 - радиуса темного кольца Ньютона в отраженном свете, R – это: - радиуса темного кольца Ньютона в отраженном свете, R – это: | |
| | радиус кривизны линзы; | 1 |
| | ширина участка клина, от которого происходит отражение света; | |
| | постоянная Ньютона. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Выберите природное явление, соответствующее интерференции света: | |
| | радужные оксидные пленки на металле; | 1 |
| | радуга; | |
| | красочное мерзание лазерного диска. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Выберите верное утверждение: | |
| | дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонением распространения света от законов геометрической оптики; | 1 |
| | дифракцией называется перераспределение интенсивности света в результате наложения двух или нескольких когерентных волн; | |
| | дифракцией называется явление разделение светового пучка на спектр при падении света на прозрачный диэлектрик. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Условием наблюдения дифракции является: | |
| | сравнимость размеров препятствия с длиной волны; | 1 |
| | источник света и препятствие должны находится на конечном расстоянии от преграды; | |
| | наличие дифракционной решетки. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Выберите из перечисленных явлений дифракцию: | |
| | разложение света в спектр при его падении на лазерный диск; | 1 |
| | разложение света в спектр при его падении на тонкую пленку; | |
| | радуга. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Выберите наиболее верную формулировка принципа Гюйгенса–Френеля: | |
| | любую точку пространства, до которой дошла волна, можно рассматривать как новый источник волн. Волны от этих источников являются когерентными и интерферируют между собой так, что их результирующая является как бы касательной волной всех этих элементарных волн; | 1 |
| | каждую точку среды, возбуждаемую проходящей световой волной, следует рассматривать как цент новой системы элементарных сферических волн; | |
| | колебания, приходящие в точку наблюдения от аналогичных двух соседних зон Френеля находятся в противофазе, следовательно, результирующее колебание, создаваемое каждой их зон в целом, отличается по фазе на π. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Метод зон Френеля заключается в том, что: | |
| | волновая поверхность разбивается на кольцевые зоны, так, что расстояние от краев зоны до точки наблюдения отличается на 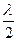 ; ; | 1 |
| | волновая поверхность разбивается на сектора с угловым размером 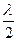 ; ; | |
| | волновая поверхность разбивается на сегменты, отстоящие друг от друга на расстоянии 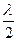 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Расстояние bm от края внешней зоні Френеля до точки наблюдения определяется соотношением: | |
| | 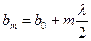 ; ; | 1 |
| | 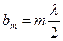 ; ; | |
| | 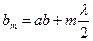 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Колебания, приходящие в точку наблюдения от аналогичных точек двух соседних зон Френеля: | |
| | находятся в противофазе; | 1 |
| | находятся в одинаковой фазе; | |
| | отличаются по фазе на 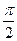 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Результирующие колебания, создаваемые каждой из соседних зон Френеля в целом, отличаются друг от друга по фазе на: | |
| | π; | 1 |
| | π/2; | |
| | 2π. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Площади зон Френеля (при малых m, где m – номер зоны): | |
| | примерно одинаковы; | 1 |
| | увеличиваются пропорционально m; | |
| | уменьшаются с увеличением m. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Радиус зоны Френеля определяется по формуле 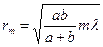 , где: , где: | |
| | а – расстояние от источника до преграды; b – расстояние от преграды до точки наблюдения; | 1 |
| | а – расстояние между четными зонами Френеля; b – расстояние между нечетными зонами Френеля; | |
| | а и b – постоянные Френеля. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Результат дифракции Френеля зависит от: | |
| | размера преграды и расстояния от преграды до экрана; | 1 |
| | размера преграды и мощности источника света; | |
| | только от размера преграды. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Пусть m – количество открытых зон Френеля, тогда, если m – нечетно, результирующая амплитуды колебаний равна: | |
| | 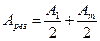 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; | 1 |
| | 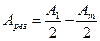 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; | |
| | 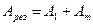 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения. , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Пусть m – количество открытых зон Френеля, тогда, если m – четно, результирующая амплитуды колебаний равна: | |
| | 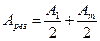 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; | |
| | 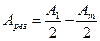 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; | 1 |
| | 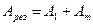 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения. , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Если преграда на пути распространения световой волны отсутствует, то результирующая амплитуда колебаний равна: | |
| | 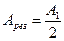 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; | 1 |
| | 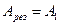 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; | |
| | 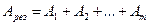 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения. , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Пластина, которая закрывает только четные или нечетные зоны Френеля называется: | |
| | зонной пластиной; | 1 |
| | собирающей пластиной; | |
| | пластиной Френеля. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Пластинки, которые открывают только четные или нечетные зоны Френеля действуют как: | |
| | собирающие линзы; | 1 |
| | рассеивающие линзы; | |
| | призмы, раскладывающие свет в спектр. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Дифракцией Френеля называется: | |
| | дифракция в сходящихся пучках, при которой источник света, преграда и точка наблюдения находятся на конечном расстоянии и которую можно наблюдать невооруженным глазом. | 1 |
| | дифракция в сходящихся пучках, при которой источник света, преграда и точка наблюдения удалены в бесконечность. | |
| | дифракция в параллельных лучах. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Выберите верное выражение для дифракционного максимума Фраунгофера при падении света на одну щель: | |
| | 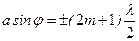 ; ; | 1 |
| | 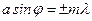 ; ; | |
| | 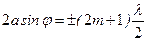 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Выберите верное выражение для дифракционного максимума Фраунгофера при падении света на одну щель: | |
| | 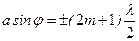 ; ; | |
| | 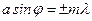 ; ; | 1 |
| | 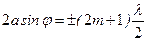 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | При наблюдении дифракции Фраунгофера от одной щели увеличение ширины щели приводит к тому, что: | |
| | полос становится больше, а они сами - ярче и уже; | 1 |
| | полос становится меньше, а они сами – ярче и уже; | |
| | количество полос и их яркость не изменяется. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Дифракционной решеткой называется: | |
| | система щелей одинаковой ширины, располагающихся на строго постоянных расстояниях друг от друга; | 1 |
| | система взаимноперпендикулярных щелей, расположенных на строго постоянных расстояниях; | |
| | сферическая система с нанесенными непро | |
| | пластинка, которая открывают только четные или нечетные зоны Френеля. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Периодом дифракционной решетки называется: | |
| | расстояние между двумя эквивалентными точками соседних щелей; | 1 |
| | время прохождения световой волной одного прозрачного для света участка; | |
| | количество щелей на единицу длины (N/d). | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Период решетки измеряется в: | |
| | м; | 1 |
| | с; | |
| | штрих /м. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Увеличение числа щелей дифракционной решетки приводит к тому, что дифракционная картина: | |
| | становится отчетливее, увеличивается интенсивность главных максимумов и уменьшается их ширина; | 1 |
| | становится отчетливее, увеличивается ширина главных максимумов; | |
| | становится отчетливее, уменьшается интенсивность главных максимумов и уменьшается их ширина. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Выберите верную формулу дифракционной решетки: | |
| | 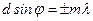 ; ; | 1 |
| | 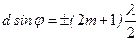 ; ; | |
| | 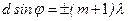 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В формуле дифракционной решетки d – это: | |
| | период решетки; | 1 |
| | расстояние от решетки до точки наблюдения; | |
| | дифракционная постоянная. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В формуле дифракционной решетки λ – это: | |
| | длина волны падающего излучения; | 1 |
| | расстояние от решетки до точки наблюдения; | |
| | дифракционная постоянная. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В формуле дифракционной решетки k – это: | |
| | порядок дифракционного максимума; | 1 |
| | номер зоны Френеля; | |
| | длина волны. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В формуле дифракционной решетки φ – это: | |
| | угол отклонения от прямолинейности распространения света; | 1 |
| | начальная фаза падающей на решетку волны; | |
| | угол падения света на дифракционную решетку. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Дисперсия дифракционной решетки определяет: | |
| | угловое или линейное расстояние между спектральными линиями, отличающимися по длине волны на единицу;; | 1 |
| | минимальную разность длин волн dλ, при которой две линии воспринимаются в спектре раздельно; | |
| | отношение длин волн линий, которые воспринимаются в спектре раздельно. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Угловой дисперсией называется величина: | |
| | 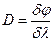 , где , где 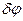 - угловое расстояние между спектральными линиями, отличающимися по длине волны на - угловое расстояние между спектральными линиями, отличающимися по длине волны на 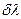 ; ; | 1 |
| | 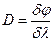 , где , где 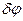 - разность фаз между волнами, спектральные линии которых отличаются по длине волны на - разность фаз между волнами, спектральные линии которых отличаются по длине волны на 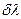 ; ; | |
| | 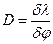 , где , где 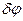 - угловое расстояние между спектральными линиями, отличающимися по длине волны на - угловое расстояние между спектральными линиями, отличающимися по длине волны на 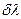 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Угловая дисперсия: | |
| | обратно пропорциональна периоду решетки ( 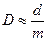 ); ); | 1 |
| | прямопропорциональна периоду решетки ( 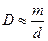 ); ); | |
| | не зависит от периода решетки. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Линейной дисперсией называется величина: | |
| | 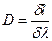 , где , где 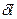 - линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на - линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на 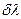 ; ; | 1 |
| | 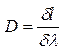 , где , где 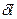 - оптическая разность хода между лучами, спектральные линии которых отличаются по длине волны на - оптическая разность хода между лучами, спектральные линии которых отличаются по длине волны на 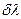 ; ; | |
| | 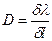 , где , где 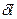 - линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на - линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на 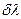 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Разрешающая сила дифракционной решетки определяет: | |
| | угловое или линейное расстояние между спектральными линиями, отличающимися по длине волны на единицу;; | |
| | минимальную разность длин волн dλ, при которой две линии воспринимаются в спектре раздельно; | 1 |
| | отношение длин волн линий, которые воспринимаются в спектре раздельно. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Критерий Релея: | |
| | две линии считаются разрешенными, если середина одного из максимумов совпадает с краем другого; | 1 |
| | две линии считаются разрешенными, если края их максимумов совпадают; | |
| | две линии считаются разрешенными, если их максимумы не совпадают. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Для дифракционной решетки разрешающая сила равна: | |
| | 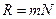 , где m – порядок спектра, N – число щелей решетки; , где m – порядок спектра, N – число щелей решетки; | 1 |
| | 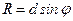 , где d – период решетки, φ – угол отклонения от прямолинейного распространения света; , где d – период решетки, φ – угол отклонения от прямолинейного распространения света; | |
| | 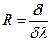 , где , где 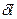 - линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на - линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на 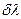 . . | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Формула Вульфа Бреггов: 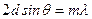 - определяет: - определяет: | |
| | положение дифракционных максимумов при падении рентгеновского излучения на кристалл; | 1 |
| | положение дифракционных максимумов при падении света на две дифракционные решетки; | |
| | положение дифракционных максимумов при падении света на систему дифракционных решеток, отстоящих на расстоянии 2d друг от друга. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В формуле Вульфа Бреггов: 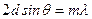 , d - это: , d - это: | |
| | расстояние между кристаллографическими плоскостями кристалла; | 1 |
| | расстояние между атомами кристалла; | |
| | расстояние от кристалла до источника излучения. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | В формуле Вульфа Бреггов: 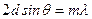 , θ - это: , θ - это: | |
| | угол скольжения (угол между направлением падающих лучей и кристаллографической плоскостью); | 1 |
| | угол падения (угол между направлением падения лучей и нормалью к кристоллаграфической плоскости); | |
| | угол отражения (угол между нормалью к кристаллографической плоскости и направлением отраженных лучей). | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Естественным называется свет: | |
| | со всевозможными равновероятными ориентациями вектора 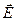 ; ; | 1 |
| | со всевозможными значениями амплитуды вектора 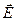 ; ; | |
| | распространяющийся в вакууме или воздухе. | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| | Поляризованным называется свет: | |
| | в котором колебания светового вектора упорядочены каким-то образом; | 1 |
| | в котором колебания светового вектора отсутствуют; | |
| | в |
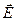 и
и 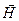 - напряженности электрического и магнитного полей;
- напряженности электрического и магнитного полей; 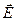 и
и 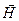 - напряженности электрического и магнитного полей.
- напряженности электрического и магнитного полей. 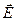 - напряженности электрического поля;
- напряженности электрического поля; 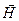 - напряженности магнитного поля;
- напряженности магнитного поля; 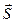 - вектора Умова-Пойтинга.
- вектора Умова-Пойтинга. 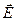 как составляющая электромагнитной волны;
как составляющая электромагнитной волны; 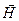 как составляющая электромагнитной волны;
как составляющая электромагнитной волны; 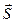 , определяющий плотность потока электромагнитной энергии.
, определяющий плотность потока электромагнитной энергии. 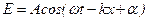 , где
, где 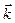 определяет:
определяет: 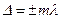 ;
; 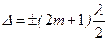 ;
; 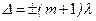 .
. 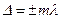 ;
; 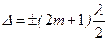 ;
; 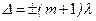 .
. 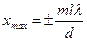 , где m – это:
, где m – это: 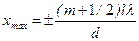 , где l – это:
, где l – это: 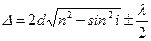 ;
; 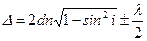 ;
; 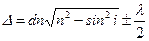 .
. 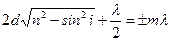 ;
; 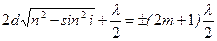 ;
; 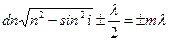 .
. 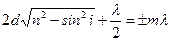 ;
; 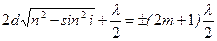 ;
; 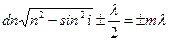 .
. 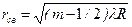 ;
; 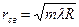 ;
; 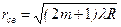 .
. 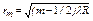 ;
; 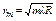 ;
; 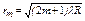 .
. 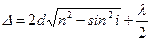 слагаемое «
слагаемое « 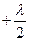 » определяет:
» определяет: 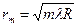 - радиуса темного кольца Ньютона в отраженном свете, R – это:
- радиуса темного кольца Ньютона в отраженном свете, R – это: 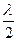 ;
; 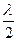 ;
; 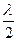 .
. 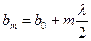 ;
; 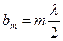 ;
; 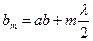 .
.  .
. 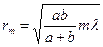 , где:
, где: 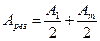 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения;
, где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; 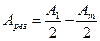 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения;
, где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; 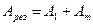 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения.
, где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения. 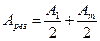 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения;
, где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; 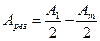 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения;
, где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения; 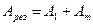 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения.
, где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения. 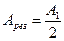 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения;
, где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; 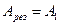 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения;
, где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; 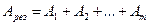 , где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения.
, где А1 – амплитуда, возбуждаемая 1-й зоной в точке наблюдения; Аm - амплитуда, возбуждаемая m-й зоной в точке наблюдения. 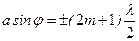 ;
; 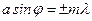 ;
; 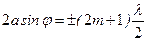 .
. 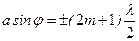 ;
; 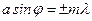 ;
; 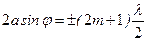 .
. 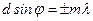 ;
; 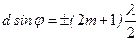 ;
; 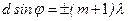 .
. 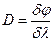 , где
, где 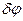 - угловое расстояние между спектральными линиями, отличающимися по длине волны на
- угловое расстояние между спектральными линиями, отличающимися по длине волны на 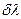 ;
; 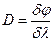 , где
, где 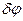 - разность фаз между волнами, спектральные линии которых отличаются по длине волны на
- разность фаз между волнами, спектральные линии которых отличаются по длине волны на 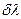 ;
; 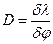 , где
, где 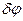 - угловое расстояние между спектральными линиями, отличающимися по длине волны на
- угловое расстояние между спектральными линиями, отличающимися по длине волны на 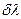 .
. 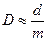 );
); 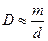 );
); 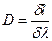 , где
, где 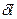 - линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на
- линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на 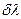 ;
; 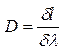 , где
, где 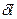 - оптическая разность хода между лучами, спектральные линии которых отличаются по длине волны на
- оптическая разность хода между лучами, спектральные линии которых отличаются по длине волны на 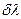 ;
; 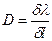 , где
, где 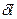 - линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на
- линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на 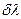 .
. 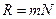 , где m – порядок спектра, N – число щелей решетки;
, где m – порядок спектра, N – число щелей решетки; 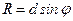 , где d – период решетки, φ – угол отклонения от прямолинейного распространения света;
, где d – период решетки, φ – угол отклонения от прямолинейного распространения света; 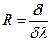 , где
, где 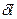 - линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на
- линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на 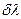 .
. 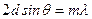 - определяет:
- определяет: 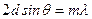 , d - это:
, d - это: 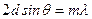 , θ - это:
, θ - это: 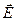 ;
; 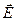 ;
; 