Система с теплообменом. Каноническое распределение Гиббса.

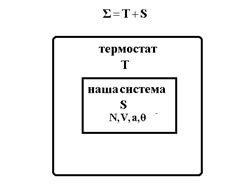
Рассмотрим теперь случай, когда изучаемая система находится в равновесии с очень большим по сравнению с ней термостатом, с которым она может обмениваться энергией, но не может обмениваться частицами. В этом случае наша система отделена от термостата оболочкой, которая с одной стороны непроницаема для частиц, а с другой стороны никак не мешает взаимодействию нашей системы с термостатом, не связанному с обменом частицами.

При таком задании нашей системы мы фиксируем число частиц в ней 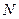, ее объем 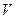и остальные внешние параметры .

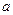Обозначим термостат буквой Т, нашу систему – буквой S, а совокупность “наша система +термостат” буквой .

Система является замкнутой. Состояние равновесия замкнутой системы определяется ее энергией. Обозначим энергию системы буквой .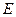

Микросостояния нашей системы и термостата, возможные в заданном состоянии равновесия ,определяются условием

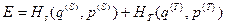. (14)

Величина E есть заданная условием задачи константа. Она определяет состояние равновесия всей замкнутой системы.

Распределение вероятности различных микросостояний такой системы называется каноническим. Теорему, определяющую функцию канонического распределения, часто называют теоремой Гиббса.

Для теоремы Гиббса принципиальное значение имеют три следующих момента. Первый момент заключается в том, что система является замкнутой. Это означает, что ее распределение является микроканоническим. Этот обстоятельство является отправной точкой теоремы Гиббса. Второй момент – это обсужденная выше аппроксимация Гамильтониана. Поэтому, когда в наших рассуждениях нам встретится функция Гамильтона составной системы мы должны будем ее заменить на сумму функции Гамильтона нашей системы и функции Гамильтона термостата. Третий момент состоит в том, что наша система 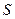очень мала по сравнению со всей системой так, что с подавляющей вероятностью реализуются такие микросостояния нашей системы, в которых ее энергия существенно меньше энергии системы : 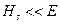. Это дает нам малый параметр, по которому, естественно, нужно будет проводить разложение в ряд.

Итак, при доказательстве теоремы Гиббса мы исходим из того, что распределение системы по ее микросостояниям является микроканоническим. Т.е. мы принимаем на веру, что функция распределения системы (зависит она как от микросостояния нашей системы, так и от микросостояния термостата) есть нормировочная постоянная 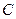, умноженная на дельта-функцию, аргумент которой есть функция Гамильтона системы минус 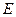. Энергия 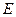есть заданная условием задачи константа.

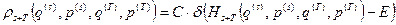. (15)

Цель теоремы Гиббса состоит в том, чтобы отталкиваясь от этой отправной точки, получить функцию распределения нашей системы .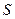

Нас интересует вероятность 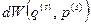нахождения нашей системы в элементарной окрестности точки 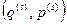ее фазового пространства, при всех микросостояниях термостата, возможных в данном состоянии равновесия.

Нам известна функция распределения составной системы . Поэтому первым делом мы должны интересующую нас вероятность выразить через эту функцию распределения. Для этого, очевидно, нужно воспользоваться теоремой о сложении вероятностей. В соответствии с этой теоремой интересующая нас вероятность есть

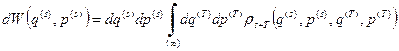. (16)

Подставляем в это выражение явный вид функции распределения составной системы . В результате получаем

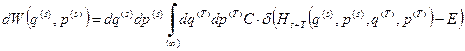. (17)

Теперь естественно воспользоваться аппроксимацией Гамильтониана. Заменяем функцию Гамильтона замкнутой системы на сумму гамильтониана нашей системы 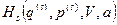и гамильтониана термостата 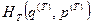. В результате выражение для нашей вероятности принимает вид

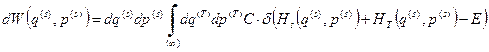. (18)

Этот интеграл легко вычислить, благодаря наличию в нем дельта-функции. Для того, чтобы его посчитать, нужно, используя сформулированную ранее теорему, перейти от интегрирования по фазовому пространству к интегрированию по энергии и, затем, воспользоваться основным свойством дельта-фукнции. После этих несложных выкладок мы получим

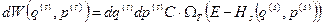. (19)

Здесь

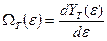, (20)

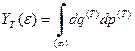. (21)

- объем фазового пространства термостата, ограниченный изоэнергетической поверхностью .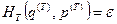

Теперь воспользуемся пользуемся тем, что наша система 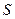по предположению есть малая часть составной системы так, что с подавляющей вероятностью реализуются микросостояния нашей системы с энергией 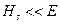. Это дает нам возможность 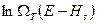разложить в ряд Тейлора в окрестности точки 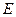. Ограничимся в этом разложении первой степенью 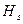. Для практических приложений этого более, чем достаточно.

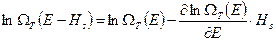. (22)

Отсюда

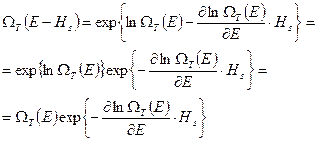(23)

Соответственно, выражение для нашей вероятности принимает вид

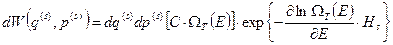. (24)

Выяснение вопроса о том, почему мы раскладываем в ряд именно 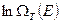, а не саму величину 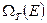, давайте отложим до того времени, когда мы будем рассматривать нашу задачу с позиций квантовой механики.

Величина 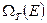не зависит от микросостояния нашей системы и поэтому может быть включена в нормировочный множитель вероятности 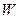. Давайте весь этот нормировочный множитель обозначим .

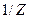Таким образом, мы получаем

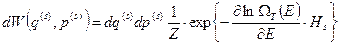. (25)

Число 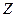определяется условием нормировки.

Введем величину

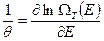. (26)

Эта величина также не зависит от микросостояния нашей системы, а определяется макроскопическим состоянием всей замкнутой системы, т.е. главным образом термостатом, поскольку по сравнению с нашей системой он просто огромен. Эта величина 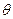называется модулем канонического распределения.

Итак, мы приходим к следующему выражению для функции распределения нашей системы

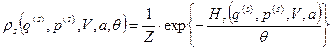. (27)

Постоянная 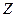определяется из условия нормировки, которое, напомню, имеет следующий вид

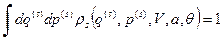. (28)

Часто эту постоянную называют статистическим интегралом данного состояния равновесия нашей системы.

Подставляя в условие нормировки явный вид функции распределения, получаем, что статистический интеграл

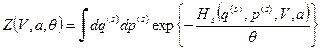. (29)

Как не сложно видеть из этого выражения, значение статистического интеграла однозначным образом определяется внешними параметрами нашей системы и модулем канонического распределения.

Таким образом, если мы знаем внешние (силовые) параметры и модуль канонического распределения, то этой информации достаточно для того, чтобы написать функцию распределения и, соответственно, вычислить все ее внутренние термодинамические параметры.