Лабораторная работа № 5 Изучение температурной зависимости сопротивления полупроводников.

Цель работы:Исследовать температурную зависимость электропроводности металлов.

Требуемое оборудование, входящее в состав модульного учебного комплекса МУК-ТТ1:

1. Блок амперметра-вольтметра АВ1 1 шт.

2. Блок генератора напряжений ГН1 1 шт.

3. Стенд с объектами исследования С3-ТТ01 1 шт.

4. Соединительные провода с наконечниками Ш4-Ш1.6 6 шт.

Краткое теоретическое введение.

Полупроводниковыми называются материалы, удельная проводимость которых имеет промежуточные значения между проводимостями металлов и диэлектриков. Структура энергетических зон полупроводников такова, что при абсолютном нуле температуры валентная зона у них заселена полностью, а зона проводимости полностью свободна. Их разделяет запрещенная энергетическая зона шириной порядка одного электронвольта (рис. 1).

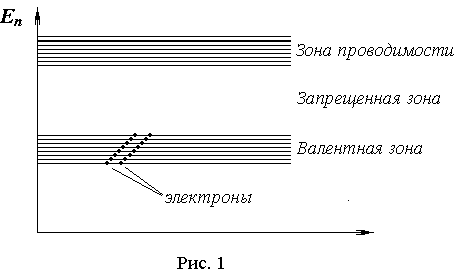
С ростом температуры тепловые флуктуации перебрасывают часть электронов из валентной зоны в зону проводимости. В валентной зоне на их месте остаются дырки, и те и другие участвуют в переносе заряда, и полупроводник становится проводящим (рис. 2).

В состоянии термодинамического равновесия число электронов N₁, перебрасываемых из валентной зоны в зону проводимости подчиняется распределению Больцмана, т.е.

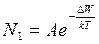(1)

где A=const, ∆W - ширина запрещенной зоны или энергия активации полупроводника, k=1.38·10^-23 Дж/К - постоянная Больцмана, Т - абсолютная температура полупроводника.

В то же время имеют место и обратные переходы, т.е. электроны возвращаются назад из зоны проводимости в валентную зону и при этом рекомбинируют с дырками. Число рекомбинирующих пар N₂ пропорционально как концентрации n свободных электронов (в зоне проводимости), так и концентрации дырок, которые между собой равны, т.е.

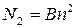(2)

В состоянии термодинамического равновесия N₁=N₂, т.е.

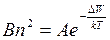(3)

Очевидно, что концентрация электронов в зоне проводимости должна удовлетворять условию:

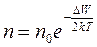(4)

где 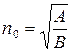константа, характеризующая материал полупроводника.

Согласно электронной теории

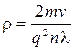(5)

где ρ- удельное сопротивление, m - масса электрона, q - его заряд, v – средняя скорость теплового движения электронов, λ - длина свободного пробега, n -концентрация свободных электронов.

Из выражений (4) и (5) следует, что

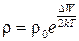(6)

где 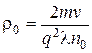величина, слабо зависящая от температуры и ее в условиях нашего опыта можно считать постоянной. Если на опыте определить зависимость сопротивления полупроводника от температуры, то с помощью выражения (6) можно найти ширину запрещенной зоны ∆W для данного материала, т.е. определить энергию его активации.

Для удобства расчетов выражение (6) необходимо последовательно прологарифмировать и продифференцировать, т.е. привести к виду

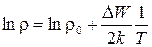	(7)
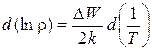	(8)

Поскольку R =rl/S, то d(lnr) = d(lnR) Переходя от дифференциалов к конечным приращениям можно записать:

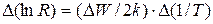	(9)
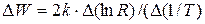	(10)

Выражение (10) и будет использовано для определения ширины запрещенной зоны исследуемого полупроводника прибора - термистора.