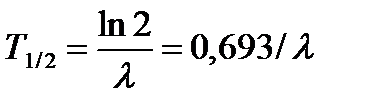Что называется периодом полураспада?

Филиал Федерального автономного образовательного учреждения

Высшего профессионального образования

«Национальный исследовательский ядерный университет «МИФИ»

Заочный факультет

Кафедра ядерной физики

Лабораторная работа №2

Тема: Исследование искусственной радиоактивности

Выполнил:

студент группы ЭиА-С12-з

Казаков Е.И.

Проверил: Гончарова И.Н.

Обнинск 2015

Цель работы: определение периода полураспада ¹¹⁶In.

Ход работы:

Рисунок 1.1 - Блок схема установки для измерения наведенной активности

1. Образец, содержащий ¹¹⁶In;

2. Счетчик излучения;

3. Свинцовый защитный контейнер для уменьшения фона;

4. Источник питания детектора;

5. Измерительное устройство;

6. Печатающее устройство

В данной работе активация образца ¹¹⁵In осуществляется нейтронами, которые замедляются в баке с водой. Активация осуществляется в реакции радиационного захвата

n + ¹¹⁵In →¹¹⁶In + γ,

которая является типичным примером так называемой резонансной реакции. Сечение этой реакции представлено на рисунке 1.2, где отчетливо виден резонанс при энергии нейтронов, равной 1,46 эВ. Большая величина этого резонанса приводит к тому, что активация, в основном обусловлена поглощением нейтронов, энергия которых в процессе замедления близка к величине 1,46 эВ.

Рисунок 1.2 – Сечение реакции n + ¹¹⁵In →¹¹⁶In + γ

После захвата нейтрона образуется неустойчивое нейтронно-избыточное ядро ¹¹⁶In, которое сдвигается с дорожки стабильности и распадается по следующей схеме:

¹¹⁶In →β^- + ν + ¹¹⁶Sn*

Образующееся в результате β-распада ядро ¹¹⁶Sn* возбуждено. Освобождение от избыточной энергии и переход в стабильное состояние ¹¹⁶Sn сопровождается γ-излучением. С громадным запасом можно считать, что γ-излучение сопровождает β-распад мгновенно. Поэтому для измерения периода полураспада можно использовать как β-, так и γ-излучение в зависимости от типа применяемого реактора.

Обычно для определения периода полураспада измеряется постоянная распада λ:

А (t) = λN(t).

Определение числа атомов, содержащихся в образце, выполняется методами химического анализа и требует продолжительного времени. Кроме того, необходимо измерение абсолютной активности образца. По этим причинам такой метод определения может быть использован, если λ очень мало, когда уменьшением N за время опыта можно пренебречь. Если λ достаточно велико, то его можно определить по формуле:

А (t) =А₀e^-λr

измеряя уменьшение активности в зависимости от времени. Весьма простой способ непосредственно определения T_1/2 заключается в измерении времени t = T_1/2, необходимого для уменьшения активно наполовину. Этот метод дает хорошие результаты, если время измерения активности Δt<<T_1/2 , а измеренное за этот промежуток времени количество ядер ΔN, испытавших распад, обеспечивает необходимую статистическую точность определения T_1/2 .

ΔN = ε∙G∙k∙A∙ Δt,

где ε – эффективность регистрации измеряемого излучения;

G – геометрический фактор, равный доле частиц, испущенных образцом и попавших в детектор;

k – среднее число частиц, которые используются для измерения, испускаемых на один акт распада.

Если во время измерений взаимное расположение счетчика и образца остается неизменным, а рабочий режим счетчика поддерживается постоянным с высокой точностью, то произведение m= ε∙G∙k не будет зависеть от времени. Следовательно, число отсчетов ΔN за время Δt будет прямо пропорционально активности образца А (t) в данный момент времени, то есть скорость счета равна

ṅ(t) = ΔN(t)/Δt = mA(t)

и будет экспоненциально уменьшаться за время опыта.

Ход работы:

Расчет дозы облучения:

t=3600 c

D_a=500 МэВ

D_b,5 = D_b/5 = 25

D_b = D_а/4 = 125

Ф_d = D_b/ D_max = 5,58∙10⁹

ф_d = Ф_d/t =155∙10⁴

r_min = (I_β/4π ф_d) = 0,02

N_ф = 15

Интервал – 60 секунд, время одной экспозиции 50 секунд, пауза 10 секунд

Таблица 1 - Таблица данных:

№	интервал	Ni	ln(Ni – Nф )	2σ (Yi)
			8.51	0,03
			8,48	0,03
			8,48	0,03
			8,47	0,03
			8,46	0,03
			8,45	0,03
			8,44	0,03
			8,44	0,03
			8,42	0,03
			8,40	0,03
			8,39	0,03
			8,37	0,03
			8,36	0,03
			8,36	0,03
			8,34	0,03
			8,32	0,03
			8,30	0,03
			8,29	0,03
			8,29	0,03
			8,27	0,03
			8,26	0,03
			8,27	0,03
			8,25	0,03
			8,22	0,03
			8,20	0,03
			8,21	0,03
			8,15	0,03
			8,15	0,03
Продолжение табл.1
			8,14	0,03
			8,17	0,03
			8,13	0,03
			8,10	0,03
			8,11	0,03
			8,10	0,03
			8,06	0,03-0,04
			8,07	0,03-0,04
			8,05	0,04
			8,03	0,04
			8,01	0,04
			8,04	0,04
			8,02	0,04
			8,02	0,04
			7,98	0,04
			7,99	0,04
			7,93	0,04
			7,90	0,04
			7,93	0,04
			7,91	0,04
			7,90	0,04
			7,87	0,04

2σ(α₁) = 0,0084

2σ(α₂) = 0

Критерий согласия = 36,71

Рисунок 1 – Графическое представление результатов измерений

Вывод: вычисленный период полураспада - практически совпал с его теоретическим значением равным 54,29 мин.

Контрольные вопросы:

Что называется периодом полураспада?

Период полураспада T_1/2—время, за которое исходное число радиоактивных ядер в среднем уменьшается вдвое.