Второй закон термодинамики

Удельная теплоемкость и ее виды. Удельной теплоемкостью с называют количество теплоты q, которое требуется для изменения температуры единицы количества вещества на 1 градус: с = q/ΔT, с = = dq/dT.

В зависимости от способа измерения единицы количества вещества, характера термодинамического процесса и величины интервала температур различают несколько видов удельных теплоемкостей.

1. В зависимости от единицы количества вещества — 1 кг, 1 м³, 1 кмоль удельную теплоемкость различают:

- массовая удельную теплоемкость с [Дж/(кг • К)];

- объемная удельную теплоемкость с' [Дж/(м³ ■ К)];

- мольная удельную теплоемкость с 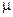[Дж/(кмоль • К)].

Связь между ними выражается следующей зависимостью

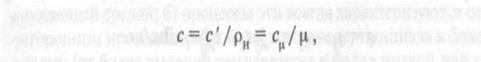
где р_н — плотность при нормальных физических условиях.

Количество теплоты определяется соответственно

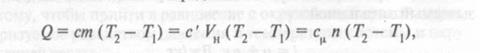
где т — масса газа; V_H — объем газа, приведенный к нормальным физическим условиям; п — число молей газа.

2. Удельная теплоемкость зависит от характера термодинамического процесса, т.е. от способа подвода теплоты удельную теплоемкость различают:

- теплоемкость при постоянном давлении (изобарную) с_р;

- теплоемкость при постоянном объеме (изохорную) c_v.

Понятия «теплоемкость при постоянной температуре» и «адиабатная теплоемкость» редко применяются, так как при Т= const означает, что теплообмен с окружающей средой отсутствует.

Отношение к= с_р/ c_v называют показателем адиабаты.

3. Поскольку теплоемкость изменяется с температурой, в зависимости от интервала температур удельную теплоемкость различают:

- истинную с;

- среднюю с_т .

Истинной называют удельную теплоемкость, соответствующую бесконечно малому интервалу температур:

с = dq / dT.

Средней называют удельную теплоемкость, соответствующую конечному интервалу изменения температуры:

с_т = q/(T₂ — Т₁,).

При практических расчетах обычно пользуются табличными данными средних теплоемкостей в интервале температур от 0 до t °С.

В этом случае количество теплоты, необходимое для нагрева 1 кг рабочего тела от 0 до t₁ °С или до t₂ °С, составит

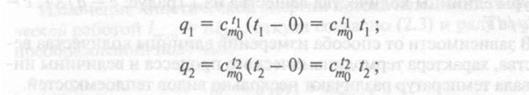
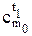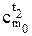где и — табличные значения теплоемкостей в интервалах температур (0 — t₁ °С) и (0 — t₂ °С).

Количество теплоты, необходимое для нагрева 1 кг тела от t₁, до t₂, определяется как разность

q=q₂ - q₁ = 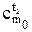t₂ - 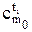t₁ , Дж/кг.

Энтальпия. В ряде случаев оказывается целесообразным объединение параметров и и рv в общий калорический параметр, называемый энтальпией:

i = и + pv, Дж/кг.

Энтальпия — термодинамическая функция, имеющая смысл полной (внутренней и внешней) энергии системы. Она складывается из внутренней энергии и и внешней упругой энергии рv, обусловленной наличием внешнего давления окружающей среды р, т.е. pv — работа, которую надо затратить, чтобы ввести рабочее тело объемом v в среду, имеющую давление р.

Энтальпия измеряется в тех же единицах, что и теплота, работа и внутренняя энергия, т.е.Дж/кг.

Энтропия.В термодинамике пользуются еще одним параметром состояния рабочего тела — энтропией, устанавливающей связь между количеством теплоты q и температурой Т (Р. Клаузиус, 1850).

Обозначают энтропию газа через S и выражают в Дж/К. Энтропию, отнесенную к 1 кг газа, называют удельной энтропией газа, и обозначают через s и выражают в Дж/(кг·К).

Тогда , количество теплоты, участвующее в том или ином термодинамическом процессе при изменении рабочеготела от состояния Т1 до Т2, можно выразить следующим образом:

.

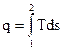Для получения решения на практике пользуются функциональной зависимостью между T и s , которую называют Т,s-диаграммой, графическое изображение подвода теплоты выглядит следующим образом:

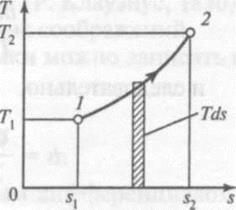
Рис. Графическое изображение подвода теплоты в Т,s-диаграммой

Энтропию нельзя измерить, ее смысл затрудительно продемонстрировать с помощью наглядных пособий, но можно понять по следующим интерпретациям.

1. Энтропия — мера ценности теплоты, ее работоспособности и технологической эффективности. Можно сказать, что для изолированной системы (нагреватель — рабочее тело) Δs = 0, при получении от нагревателя количества теплоты q₁ энтропия s₁ = q₁ /Т₁, откуда следует, что чем меньше s₁ т.е. чем выше Т₁, тем больше совершаемая системой работа.

Повседневный опыт свидетельствует, что чем температура теплоносителя выше при том же количестве теплоты q, т.е. чем меньше энтропия s= q/T, тем теплота ценнее, поскольку шире может быть использована не только для совершения работы как таковой, но и для технологических нужд — выплавки металла, отопления и т.д.

2. Энтропия — мера потери работы вследствие необратимости реальных процессов. Чем больше необратим процесс в изолированной системе, тем больше возрастает энтропия s₂ >> s₁ и тем большая доля энергии не превращается в работу, рассеивается в окружающую среду.

3. Энтропия — мера беспорядка. Если установить некоторую меру неупорядоченности макросистемы — неупорядоченности расположения и движения частиц D? то можно записать .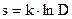

Следовательно, возрастание беспорядка означает возрастание энтропии, рассеивание энергии. При подводе теплоты увеличивается хаотичность теплового движения частиц и энтропия возрастает. Наоборот, охлаждение системы при постоянном объеме есть извлечение из нее теплоты, а следовательно, и энтропии; упорядоченность системы при этом повышается, а энтропия уменьшается.

При конденсации газа в жидкость молекулы занимают более определенные положения, упорядоченность их расположения скачкообразно увеличивается, что соответствует скачкообразному уменьшению энтропии. При дальнейшем понижении температуры тепловое движение становится все менее интенсивным, беспорядок — все меньшим, а значит, и все меньшей становится энтропия.

Когда жидкость превратится в твердое вещество, молекулы (ионы) образуют правильные кристаллические решетки, т.е. неупорядоченность опять уменьшится, а с нею уменьшится и энтропия и т.д. Такая закономерность позволяет предположить, что при нуле абсолютной температуры тепловое движение полностью прекратится и в системе установится максимальный порядок, т.е. неупорядоченность и энтропия станут равными нулю. Это предположение согласуется с опытом, но не поддается опытной проверке, идо абсолютный нуль температуры недостижим.

Второй закон термодинамики. Второй закон термодинамики, как и первый, является опытным законом, основывающимся на многовековых наблюдениях ученых. Однако установлен он был только в середине XIX в.

Наблюдения за явлениями природы показывают, что:

а) возникновение и развитие самопроизвольно протекающих в ней естественных процессов, работа которых может быть использована для нужд человека, возможно лишь при отсутствии равновесия между участвующей в процессе термодинамической системой и окружающей средой;

б) процессы эти всегда характеризуются односторонним протеканием от более высокого потенциала к более низкому (от более высокой температуры к более низкой или от более высокого давления к более низкому);

в) при протекании указанных выше процессов термодинамическая система стремится к тому, чтобы прийти в равновесие с окружающей средой, характеризуемое равенством давления и температуры системы и окружающей среды.

г) из наблюдений за явлениями природы следует также, что для того, чтобы заставить процесс протекать в направлении, обратном направлению протекания самопроизвольного процесса, необходимо затратить заимствуемую из внешней среды энергию.

Второй закон термодинамики представляет собой обобщение изложенных выше положений и заключается в том, что

1) самопроизвольное протекание естественных процессов возникает и развивается при отсутствии равновесия между участвующей в процессе термодинамической системой и окружающей средой;

2) самопроизвольно происходящие в природе естественные процессы, работа которых может быть использована человеком, всегда протекают лишь в одном направлении — от более высокого потенциала к более низкому;

3) ход самопроизвольно протекающих процессов происходит в направлении, приводящем к установлению равновесия термодинамической системы с окружающей средой, и по достижении этого равновесия процессы прекращаются;

4) процесс может протекать в направлении, обратном самопроизвольному процессу, если энергия для этого заимствуется из внешней среды.

Формулировки второго закона термодинамики, данные различными учеными, вылились в форму постулатов, полученных в результате развития положений, высказанных французским ученым Сади Карно.

В частности, постулат немецкого ученого Клаузиуса состоит в том, что тепло не может переходить от холодного тела к теплому без компенсации. Сущность постулата английского ученого Томсона заключается в том, что невозможно осуществить цикл теплового двигателя без переноса некоторого количества теплоты от источника теплоты с более высокой температурой к источнику с более низкой температурой.

Эту формулировку надо понимать так, что, для того чтобы работала периодически действующая машина, необходимо, чтобы были минимум два источника теплоты различной температуры; при этом в работу может быть превращена лишь часть теплоты, забираемой из высокотемпературного источника, в то время как другая ее часть должна быть передана низкотемпературному источнику.

4. РЕАЛЬНЫЕ ГАЗЫ, ВОДА И ВОДЯНОЙ ПАР

К реальным газам в технической термодинамике принято относить перегретые пары некоторых жидкостей. В отличие от воображаемого идеального газа реальный газ при соответствующих условиях может быть сжижен, т.е. сконденсирован, или же переведен в твердое состояние.

В технике широко применяют пары различных веществ: воды, аммиака, хлористого метила, сернистого ангидрида и др. Наибольшее применение имеет водяной пар, являющийся основным рабочим телом паровых двигателей, отопительных и других устройств. Известно, что законы идеальных газов нельзя распространить на рабочие тела, состояние которых не очень удалено от жидкой фазы.

Из ряда предлагавшихся уравнений состояния, применимых для реального газа с известной степенью приближенности, можно отметить уравнение Ван-дер-Ваальса:

,

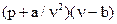где а и b — постоянные для данного газа.

Слагаемым а/v² в первом множителе учитывается влияние сил взаимодействия молекул, во втором — вычитаемым b учитывается влияние объема молекул (поскольку в идеальном газе, для которого и справедливо уравнение состояния Клапейрона, объем молекул полагается равным нулю).

Практически пользоваться уравнением Ван-дер-Ваальса нельзя, так как оно дает результаты, недостаточно точные для нужд современной паротехники. Наиболее точным является в настоящее время уравнение состояния реальных газов, разработанное М.П. Вукаловичем и Н.И. Новиковым (МЭИ) применительно в основном к водяному пару. Однако для практических целей пользование этим, как и другими уравнениями состояния реального газа, неудобно вследствие сложности их и необходимости выполнения трудоемких вычислений. Обычно пользуются готовыми данными, которые берут из таблиц водяного пара или из i,s-диаграммы водяного пара.

На современных крупных тепловых электростанциях основным двигателем является паровая турбина, где в качестве рабочего тела используется водяной пар, который получают в паровых котлах. Поэтому изучение термодинамических свойств паров рассмотрим на примере водяного пара.

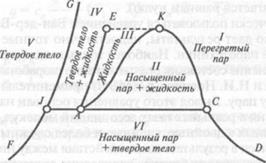
Водяной пар. На рис. 2.10 приведены фазовые состояния воды. Здесь может быть выделено несколько областей:

	Т

	s

Рис. 2.10. Фазовая диаграмма для водяного пара в Т,s-диаграмме:

I— газообразное состояние (перегретый пар, обладающий свойствами реального газа);

II— равновесное состояние воды и насыщенного водяного пара (двухфазное состояние); двухфазную область II называют также областью парообразования;

III, ограниченная изотермой ЕК, — жидкое состояние (вода);

IV— равновесное состояние твердой и жидкой фаз;

V— твердое состояние.

Области III, II и II, I отделены так называемыми пограничными линиями: левой АК и правой KD. Общая для левой и правой пограничных линий (и областей I, II и III) точка К обладает особыми свойствами и называется критической точкой. Она имеет определенные параметры р_кр, _кр и Т_{кр ,}при которых кипящая вода переходит в перегретый пар, минуя двухфазную область. Отсюда следует, что вода (точнее, ее жидкая фаза) не может существовать при температурах выше Т_кр . Будучи нагретой до этой температуры, весь объем воды практически мгновенно должен превратиться в пар. Вместе с тем пар при давлениях больших, чем р_кр, и при охлаждении до температуры Т_кр непосредственно превращается в жидкость, минуя область влажного пара.

Критическая точка воды имеет следующие параметры:

р= 22,136 МПа; Т_кр = 374,15 °С; 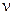_кр = 0,00326 м³/кг.

Значения р,Т, v и s для обеих пограничных линий (кипения и сухого насыщенного пара) приводятся в специальных таблицах термодинамических свойств водяного пара.

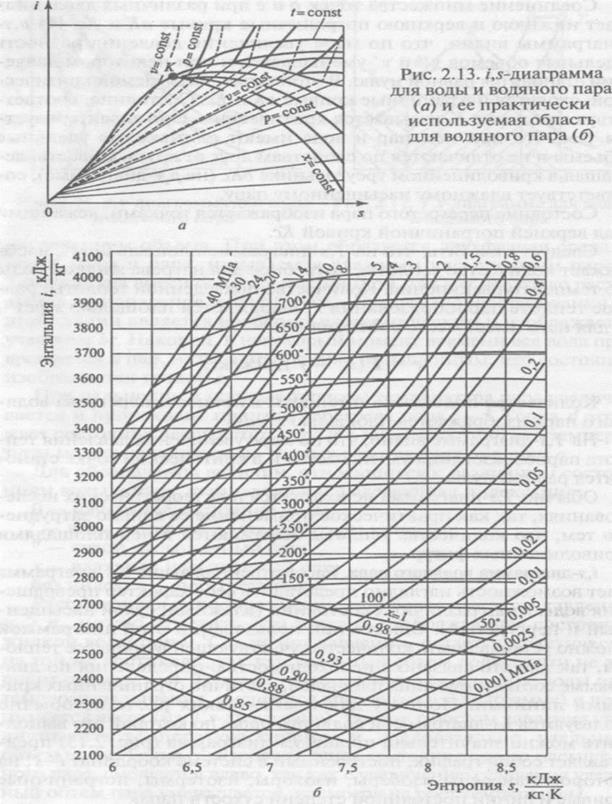
i,s-диаграмма водяного пара. Рассмотренная выше Т,s-диаграмма дает возможность наглядно представить себе характер превращения воды в пар различных состояний (влажный, сухой насыщенный и перегретый). Однако при пользовании этой диаграммой сложно устанавливать количество участвующей в процессе теплоты, так как это связано с необходимостью определения по диаграмме соответствующих площадей, частично ограниченных кривыми линиями. Поэтому для практических расчетов обычно пользуются i,s-диаграммой водяного пара, по которой это выполнить можно значительно проще.

i,s-диаграмма (рис. 2.13) представляет собой график, построенный в системе координат i—s, на котором нанесены изобары (р-const), изохоры (v-const), изотермы (t-const), пограничные кривые и линии постоянной степени сухости пара (паросодержания (х-cоnst).

Контрольные вопросы

1.Укажите основные параметры состояния рабочего тела и единицы измерения их.

2.Дайте определение средней и истинной теплоемкости, чем отличается теплоемкость с_р от с_у?

3.Объясните сущность первого закона термодинамики и напишите его математическое выражение.

4.Какова сущность второго закона термодинамики? Дайте некоторые формулировки этого закона.

5.Покажите в p,v- и Т,s-диаграммах характерные области и линии для воды и водяного пара.

6.Покажите в Т,s -диаграмме площадки, изображающие количество теплоты на подогрев воды, теплоту парообразования, теплоту на перегрев пара.