Теоретический расчет величины индукции магнитного поля

Введение

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в тонких пластинках золота.

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле 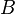течёт электрический ток под действием напряжённости 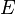. Магнитное поле будет отклонять носители заряда от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости^[1] будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.

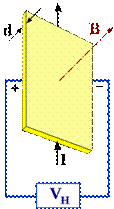
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов 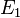не скомпенсирует магнитную составляющую силы Лоренца:

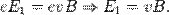
Скорость электронов 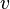можно выразить через плотность тока:

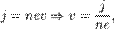
где 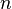— концентрация носителей заряда. Тогда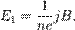

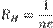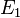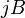Коэффициент пропорциональности между и называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак 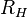, что объясняется в полуклассической и квантовой теориях твёрдого тела.

Магнитное поле постоянных токов различной формы исследовалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты их опытов были обобщены французским ученым П. Лапласом.

Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 1) индукцию поля dB, равен

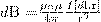(1)

где dl - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r - радиус-вектор, который проведен из элемента dl проводника в точку А поля, r - модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с направлением касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение винта совпадает с направлением тока в элементе.

Модуль вектора dB задается выражением 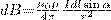(2), где α — угол между векторами dl и r.

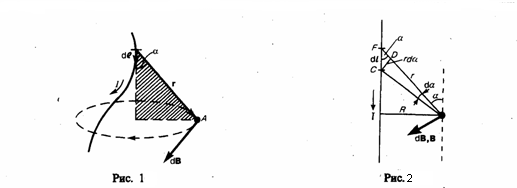
Магнитное поле в центре кругового проводника с током (рис. 166). Как видно из рисунка, каждый элемент кругового проводника с током создает в центре магнитное поле одинакового направления - вдоль нормали от витка. Значит, сложение векторов dB также можно заменить сложением их модулей. Поскольку расстояние всех элементов проводника до центра кругового тока одинаково и равно R и все элементы проводника перпендикулярны радиусу-вектору (sinα=1), то, используя (2),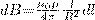

Тогда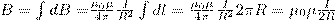

Следовательно, магнитная индукция поля в центре кругового проводника с током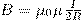

Теоретический расчет величины индукции магнитного поля

Соленоид – цилиндрическая катушка, состоящая из большого числа витков изолированной проволоки, по которой течет ток. Если шаг винтовой линии достаточно мал, то каждый виток соленоида можно заменить замкнутым витком. Линии вектора магнитной индукции внутри соленоида направлены вдоль его оси, причем вектор B составляет с направлением тока в соленоиде правовинтовую систему.

Подключим соленоид к источнику питания 5 вольт. Установим ток в обмотке соленоида I = 0,55А.

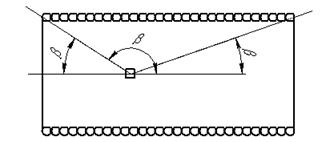Рисунок 3 – Соленоид в разрезе

Параметры соленоида:

N =200 витков

l(соленоида)=67 мм

d = 25 мм

n=200/0.067=2985витков/м

Теоретически рассчитаем величину индукции в точках соленоида:

B_x=µ₀*I*n*(cosβ₁+cosβ₃)/2 – индукция магнитного поля катушки.

Координаты точки измерения, мм

-30

-5

8,75

17,5

26,25

43,75

52,5

61,25

1. B₁=4π*10^-7*0,55*2985*(-0,923+0,992)/2=0,069*10^-3(Тл)

2. B₂=4π*10^-7*0,55*2985*(-0,371+0,986)/2=0,615*10^-3(Тл)

3. B₃=4π*10^-7*0,55*2985*(0+0,989)/2=0,984*10^-3(Тл)

4. B₄=4π*10^-7*0,55*2985*(0,574+0,987)/2=1,5*10^-3(Тл)

5. B₅=4π*10^-7*0,55*2985*(0,813+0,972)/2=1,78*10^-3(Тл)

6. B₆=4π*10^-7*0,55*2985*(0,903+0,961)/2=1,86*10^-3(Тл)

7. B₇=4π*10^-7*0,55*2985*(0,942+0,942)/2=1,88*10^-3(Тл)

8. B₈=4π*10^-7*0,55*2985*(0,962+0,903)/2=1,86*10^-3(Тл)

9. B₉=4π*10^-7*0,55*2985*(0,972+0,813)/2=1,78*10^-3(Тл)

10. B₁₀=4π*10^-7*0,55*2985*(0,987+0,574)/2=1,5*10^-3(Тл)

11. B₁₁=4π*10^-7*0,55*2985*(0,989+0)/2=0,984*10^-3(Тл)

12. B₁₂=4π*10^-7*0,55*2985*(0,986-0,371)/2=0,615*10^-3(Тл)

13. B₁₃=4π*10^-7*0,55*2985*(0,992-0,923)/2=0,069*10^-3(Тл)