Приклади розв’язування та оформлення задач
КАФЕДРА ФІЗИКИ
ЗБІРНИК ЗАДАЧ ІЗ ФІЗИКИ
ЧАСТИНА 2
для студентів
денної та заочної форм навчання

Полтава – 2004
Збірник задач із фізики. Частина 2. Для студентів інженерних спеціальностей денної та заочної форм навчання. −Полтава:ПолтНТУ, 2004. − 34 с.
Укладачі: проф. В.В.Соловйов, доц. Л.П.Давиденко, ас. О.В.Фернебок
Відповідальний за випуск: завідувач кафедри фізики
В.В.Соловйов, доктор хімічних наук, професор
Рецензент: доктор фіз.-мат. наук О.П.Руденко
Затверджено радою науково-методичною університету
Протокол № 1 від 27.01.2005 р.
Редактор Н.В.Жигилій
Коректор Н.І.Янкевич
Електрика та магнетизм. Основні закони та формули
| Закон Кулона | F =  |
| Напруженість електричного поля і потенціал | E=  ; φ = ; φ =  |
| Напруженість і потенціал точкового заряду | Е=  ; φ= ; φ=  |
| Зв’язок потенціалу з напруженістю для однорідного поля | Е=  = =  |
| Робота з переміщення заряду в електричному полі | A = q(φ1 –φ2) = qU |
| Електроємність: | |
| відокремленого провідника | C =  |
| провідної кулі | C = 4πεε0R |
| плоского конденсатора | C =  ; С= ; С=  |
| Електроємність системи конденсаторів: | |
| при послідовному з’єднанні | C =C1 +C2 + … + Cn |
| при паралельному з’єднанні |  |
| Енергія поля зарядженого плоского конденсатора | W=  |
| Сила і густина струму | I =  ; ј = ; ј =  |
| Закон Ома: | |
| для ділянки кола | I=  = =  |
| для замкнутого кола | I=  |
| Опір однорідного провідника | R= ρ  ; r= ; r=  |
| Опір системи провідників: | |
| при послідовному з’єднанні | R=R1+R2+ …+Rn |
| при паралельному з’єднанні |  |
| Закон Джоуля-Ленца | Q =I2Rt |
| Робота і потужність струму | A=IUt; P = IU |
| Закони Кірхгофа: | |
| перший |  ΣIі = 0 ΣIі = 0 |
| другий | ΣIі Rі = Σ Eі |
| Індукція магнітного поля | В = μμ0 Н |
| Закон Ампера | F = IBl sinα  |
| Сила Лоренца | F= qJB sinα  |
| Магнітний момент контура зі струмом | Pm = IS |
| Механічний (обертальний) момент, діючий на контур зі струмом | М =Pm B sinα |
| Напруженість магнітного поля: | |
| в центрі колового струму | H =  |
| прямого нескінченно довгого провідника зі струмом на відстані r | H =  |
| ділянки провідника із струмом | H =  (соsα1 – соsα2) (соsα1 – соsα2) |
| на осі нескінченно довгого соленоїда | H=nI=  I I |
| Магнітний потік однорідного магнітного поля | Ф = BS cosα |
| Робота з переміщення контура зі струмом у магнітному полі | А = I ΔФ |
| Основний закон електромагнітної індукції (закон Фарадея) |  = - N = - N  |
| Електрорушійна сила самоіндукції |  = - L = - L  |
| Індуктивність нескінченно довгого соленоїда | L =  =μμ0n2l S =μμ0n2l S |
| Енергія магнітного поля соленоїда | W=  l S l S |
| Формула Томсона | Т=2π  |
| Довжина хвилі | λ=сТ |
| Швидкість поширення електромагнітних хвиль у середовищі | J =  |
Оптика. Фізика атома й атомного ядра.
Основні закони і формули
| Показник заломлення середовища | n =  |
| Закон заломлення світла |  |
| Умова максимального посилення світла при інтерференції | ∆= ± kλ, к= 0,1,2,… |
| Умова послаблення світла | ∆= ± (2 к+1)  |
| Кільця Ньютона у відбитому світлі: | |
| радіуси темних кілець | rк =  , к =0,1,2, … , к =0,1,2, … |
| радіуси світлих кілець | rк =  , к =0,1,2,3, … , к =0,1,2,3, … |
| Умова головних максимумів дифракційної решітки | dsinφ = ± кλ, к = 0,1,2,… |
| Формула Вульфа-Брегга | 2d sinΘ= кλ |
| Ступінь поляризації світла | P =  . 100% . 100% |
| Закон Брюстера | tq iБ =  |
| Закон Малюса | I = I0 соs2φ |
| Кут обертання площини поляризації: | |
| у кристалах | φ = [α] l |
| у розчинах | φ = [α] сl |
| Залежність маси частинки від швидкості її руху | m =  |
| Повна енергія частинки | Е = mc2 |
| Кінетична енергія частинки | Ек =mc2 – m0c2 |
| Закон Стефана-Больцмана | Rэ =σ Т4 |
| Перший закон Віна (закон зміщення) | λmax =  |
| Другий закон Віна | rλmas = C2T5 |
| Енергія фотона (кванта світла) | εф = hv =  |
| Імпульс і маса фотона | Pф =  ; mф= ; mф=  |
| Рівняння Ейнштейна для зовнішнього фотоефекту | hv = А +  |
| Червона межа фотоефекту | vкр=  ; λкр = ; λкр =  |
| Тиск світла при нормальному падінні на поверхню | p=  (1+ρ) (1+ρ) |
| Формула Комптона для розсіяного фотона | ∆λ= λ’ – λ=  (1-сosΘ) (1-сosΘ) |
| Правило частот Бора | hv = Еn – Em |
| Формула Бальмера |  |
| Закон поглинання випромінювання речовиною (формула Бугера) | I = I0 e-μx |
| Довжина хвилі де Бройля | λБ =  |
| Закон радіоактивного розпаду | N = N0 e-λt |
| Активність радіоактивного ізотопа | а = λN0 e-λt = а0e-λt |
| Дефект маси ядра | Δ m=[  +(A-Z)mn –mA] +(A-Z)mn –mA] |
| Енергія зв’язку ядра | ΔЕ = Δ m c2, ΔЕ = 931 Δ m (МеB) |
| Енергетичний вихід реакції А(а,в)В | Q = 931[(mA + ma )- (mB + mв)] (МеВ) |
Для успішного розв’язання задач рекомендується така послідовність дій:
1. Приступаючи до розв’язання задачі з будь-якої теми, спочатку вивчіть теоретичний матеріал за підручником, розберіться в прикладах розв’язання типових задач.
2. Уважно прочитайте умову задачі, вникаючи в її зміст. Чітко уявіть собі фізичне явище, процеси, які відображені умовою задачі.
3. Запишіть умову задачі й величини, що шукаються в задачі. Умови записуйте ретельно, нічого не пропускаючи; вкажіть і ті величини, числові значення яких не задаються, але про них згадується в умові задачі; випишіть усі величини в умову задачі для наочності стовпчиком.
4. Ретельно виконайте креслення, що пояснює зміст задачі (в тих випадках, коли це можливо). Є деякі задачі, що розв’язуються графічно, тоді правильно виконане креслення буде розв’язанням задачі.
5. Згадайте, якому закону підпорядкований фізичний процес і якими математичними формулами він описується. Якщо формул декілька, зіставте величини, що входять в різні формули, з величинами, заданими та тими, які необхідно знайти. Якщо при розв’язанні задачі застосовується формула, що безпосередньо не відображає якого-небудь фізичного закону і визначення фізичної величини, її слід вивести, виходячи з фізичної суті процесу, який відображений в умові задачі.
6. На першому етапі розв’язуйте задачу в загальному вигляді, тобто виводьте формулу, в якій шукана величина виражена через величини, задані в умові. Винятки з цього правила вкрай рідкі і бувають в двох випадках: якщо формула якої-небудь проміжної величини настільки громіздка, що обчислення цієї величини значно спрощує подальший запис розв’язання; якщо числовий розв’язок задачі значно простіший, ніж виведення формули.
7. Перевірте, чи дає робоча формула правильну одиницю вимірювання шуканої величини. Для цього в робочу формулу слід підставити одиниці всіх величин у СІ, виконати з ними необхідні дії. Якщо одержана в результаті одиниця не збігається з одиницею шуканої величини, задача розв’язана неправильно. Якщо в обчислювальну формулу входять алгебраїчні суми, слід звернути увагу на одиниці доданків.
8. Підставте в остаточну формулу, одержану в результаті розв’язання задачі в загальному вигляді, числові значення, виражені в одиницях СІ.
9. Виконуйте обчислення згідно з робочою формулою, керуючись правилами наближених обчислень. Запишіть у відповіді числове значення і скорочену назву шуканої величини в СІ.
10. Розв’язання кожної задачі повинне супроводжуватися коротким поясненням, яке розкриває логічну послідовність операцій при її розв’язанні.
11. Одержавши шукану величину, проаналізуйте її кількісно і переконайтесь, що вона реальна в умовах даної задачі.
Приклади розв’язування та оформлення задач
Задача №1
Батарея, замкнута на резистор в 2 Ом, дає струм силою в 1,6 А. При замиканні її на резистор в 1 Ом через нього проходить струм 2 А. Знайти втрату потужності в середині батареї та ККД батареї в обох випадках.
Розв'язання
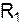 = 2 Ом Відповідно до закону Ома для повного кола:
= 2 Ом Відповідно до закону Ома для повного кола:
 = 1,6 А
= 1,6 А
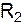 = 1 Ом I =
= 1 Ом I =  , де
, де
 = 2 А
= 2 А
_________ I − сила струму в колі, ε − ЕРС, R − опір,
 - ? Застосовуємо цей закон для обох випадків:
- ? Застосовуємо цей закон для обох випадків:  - ?
- ?
 - ?
- ?
η1 -? 
 ;
; 
(ε та r в обох формулах однакові, бо батарея одна й та сама).
Відповідно:
ε =  ; ε =
; ε =  , або
, або  .
.
Розв'яжемо рівняння відносно r:

 ,
, 


r =  .
.
Обчислимо:
r = 
За формулою N =  r (N потужність, cила струму, r внутрішній опір) обчислимо втрати потужності в обох випадках:
r (N потужність, cила струму, r внутрішній опір) обчислимо втрати потужності в обох випадках:
N  =
= 
 r; N
r; N  = 1,6
= 1,6 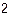 3 = 7,68 (Вт).
3 = 7,68 (Вт).
N  =
= 
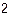 r; N
r; N  = 2
= 2 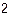 3 = 12 (Вт).
3 = 12 (Вт).
За формулою =  ( ККД, R опір, r внутрішній опір)
( ККД, R опір, r внутрішній опір)
визначимо коефіцієнт корисної дії (ККД) для обох випадків:
 =
=  ;
;  =
= 
 = 40%
= 40%
 =
=  ;
;  =
= 
 = 25%.
= 25%.
Відповідь: N  = 7,7 Вт;
= 7,7 Вт;  = 40%,
= 40%,
N  = 12 Вт;
= 12 Вт;  = 25%.
= 25%.
Задача № 2
Двократно іонізований атом гелію ( 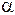 -частинка) рухається в однорідному магнітному полі напруженістю 105
-частинка) рухається в однорідному магнітному полі напруженістю 105  по колу радіусом 100 см. Знайти швидкість
по колу радіусом 100 см. Знайти швидкість 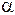 -частинки.
-частинки.
Розв'язання
q = 3,2  10
10  Кл Для
Кл Для 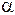 - частинки за таблицями визначаємо
- частинки за таблицями визначаємо
m = 6,64 10  кг q = 3,2 10
кг q = 3,2 10  Кл (заряд
Кл (заряд 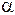 - частинки)
- частинки)
H = 10 
 m = 6,64 10
m = 6,64 10  кг (маса
кг (маса 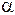 - частинки).
- частинки).
R = 100 см = 1 м На заряджену частинку, що рухається в магнітному полі, діє сила Лоренца
________________ FЛ = q VB sin 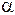 , де
, де
V - ? FЛ − сила Лоренца,
q − заряд частинки,
V − швидкість частинки,
B − індукція магнітного поля,
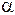 − кут між векторами
− кут між векторами  та
та  , якщо частинка рухається по колу то
, якщо частинка рухається по колу то 

 ,
, 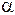 = 90
= 90 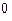 , sin
, sin 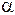 = 1.
= 1.
Індукція магнітного поля  зв'язана з напруженістю магнітного поля
зв'язана з напруженістю магнітного поля  співвідношенням: В=
співвідношенням: В= 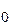 Н,
Н,
− магнітна проникність, для вакууму та повітря =1,
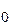 − магнітна стала,
− магнітна стала, 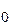 = 4π 10
= 4π 10 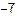 Гн/м,
Гн/м,
тобто FЛ = q V 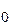 Н.
Н.
Сила Лоренца надає частинці доцентрового (нормального) прискорення, відповідно за II законом Ньютона:
mа  = FЛ, mа
= FЛ, mа  = q V
= q V 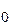 Н,
Н,
m − маса частинки, а  − нормальне прискорення.
− нормальне прискорення.
а  =
=  , де V − швидкість частинки, R − радіус кола.
, де V − швидкість частинки, R − радіус кола.
З урахуванням цього: m  = q V
= q V 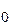 Н, виразимо V:
Н, виразимо V:
V = 
Обчислимо: V=  м/с.
м/с.
Відповідь: V= 6,1106 м/с.
Задача № 3
Під яким кутом до горизонту повинно знаходитися Сонце, щоб його промені, відбиті від поверхні озера, були б найбільш поляризовані?
Розв’язання
| n=1.33 | За законом Брюстера |
| a - ? |  , де і – кут падіння променя, n – показник заломлення. , де і – кут падіння променя, n – показник заломлення. |

 ,
,
 .
.
Відповідно  ,
,
 .
.
Відповідь: a=370.
Задача № 4
Знайти:
а) радіус першої боровської орбіти для однократно іонізованого гелію;
б) швидкість електрона на ній.
Розв’язання
Електрон у воднеподібному атомі рухається по коловій орбіті, тому кулонівська сила взаємодії електрона й ядра є доцентровою силою, тобто
 ,
,
де z – номер елемента, е – заряд електрона,  Кл, r – радіус орбіти, v – швидкість електрона на орбіті, e0 – електрична стала, m – маса електрона, m=9,1×10-31 кг.
Кл, r – радіус орбіти, v – швидкість електрона на орбіті, e0 – електрична стала, m – маса електрона, m=9,1×10-31 кг.
За другим постулатом Бора момент імпульсу електрона на будь-якій орбіті задовольняє умову:  ,
,
де n – номер орбіти, h – стала Планка, h=6.63×10-34 Дж×с, r, v – відповідно радіус орбіти та швидкість електрона на ній.
Розв’яжемо систему рівнянь:

поділимо перше рівняння на друге й отримаємо:
 або
або
 ,
,
за умовою z=2, n=1.
Відповідно:
V = 
 =
=  ,
,
розрахуємо:
 .
.
З другого постулату Бора визначимо радіус орбіти:
 ,
,
відповідно:
 ,
,
якщо n=1, то
 ,
,
розрахуємо:
 (м).
(м).
Відповідь:  ,
,  м.
м.
