Учитывая пропорцию (2.15), получим

,

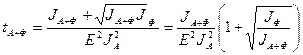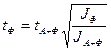(2.18)

Если отношение J_Ф/J_А+Ф<<1, то последняя формула становится проще –

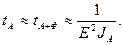(2.19)

С помощью формул (2.18) и (2.19) искомую продолжительность времени наблюдения находят следующим образом. Скорости счета J_Ф и J_А+Ф измеряют в течение 1-2 минуты, и найденные значения подставляют в одну из последних формул. Подстановка дает возможность определить необходимый интервал времени, измерения в пределах которого обеспечивают заданную относительную ошибку. Произвести эти измерения. С учетом фона результат измерения скорости счета от препарата записывают в виде

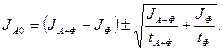(2.20)

В тех случаях, когда скорость счета J_А+Ф значительно больше J_Ф, последняя формула становится проще

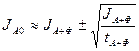. (2.21)

Если измерения проводятся несколько раз (имеется К-мерная выборка), то, записывая результат, следует учесть формулу (2.10).

Распределение Гаусса является предельным случаем распределения Пуассона и многих других законов распределения. Рассмотрим распределение Пуассона при больших n₀ и n. Дискретность распределения по n в этом случае теряет свое значение, так как n меняется практически непрерывно. Будем характеризовать отличие n от n₀ с помощью e, определенного соотношением

.

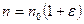Подставляя формулу Стирлинга [см. вывод (1.10)]

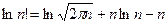
в выражение (2.3), найдем

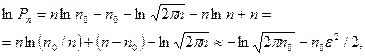
(учтено разложение натурального логарифма в ряд при n₀/n »1) откуда

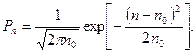(2.22)

Учтем формулу (2.6) и перепишем (2.22) в виде

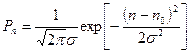. (2.23)

Это последнее распределение называют распределением Гаусса с максимумом вероятности P_n при n=n₀ . Если случайная величина имеет нормальную плотность вероятности с неизвестным средним n₀ и неизвестной дисперсией s², то на основе метода максимального правдоподобия для К-мерной выборки имеем:

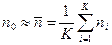, (2.24)

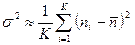. (2.25)

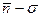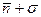Полученные формулы позволяют сделать вывод о том, что с вероятностью 68% истинная величина n₀ находится в интервале от до . Результат определения n₀ запишем в виде

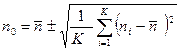. (2.26)

Если все измерения в выборке сделаны с постоянным интервалом времени t, то для скорости счета имеем

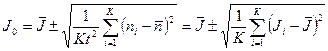. (2.27)

При большом числе измерений результаты определения средней квадратической ошибки в предположении выполнимости законов распределения Пуассона и Гаусса вероятно совпадут.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Работа может быть выполнена на различных лабораторных уста­новках с использованием различных детекторов ионизирующих излучении (счетчиков частиц или квантов) и различных регистрирующих приборов

Целью работы является определение ошибки, возникающей при из­мерении,радиоактивности, а также измерение числа импульсов с заданной степенью точности при изучении активности одного или нескольких нуклидов. В качестве источников ионизирующего излучения могут быть взяты несколько препаратов различной активности или один препарат, еслиусловияпроведения эксперимента позволяют регулировать интенсивность по­тока попадающих в счетчик ионизирующихчастиц или квантов путём их частичного поглощения.

Перед выполнением работы следуетвыяснить, какой комплект аппаратуры будет использован для проведенияизмерений; какие источники необходимы для выполнения поставленной задачи; в течение каких интервалов времени следует проводить измерения.

При выполнении работы рекомендуется следующий порядокдействий.

I. Изучить описание лабораторного комплекта аппаратуры и инструкцию по работе с ним.

2. С разрешения преподавателя включить в сеть приборы комплекта, подготовитьих к проведению измерений.

3. Произвести измерениерадиационного фона в течение нескольких минут с учётом заданной преподавателем относительной ошибки. Вычислить скорость счётафона J_Ф=N_Ф/t_Ф.

4. Выяснить, как изменяется среднеквадратическая ошибка измерения числа импульсов при изучении активности при увеличении времени измерения. Для этого один раз измерить число импульсов от препарата №1 в течение 1 минуты, второй раз – в течение 2-х – 5-ти минут и третий раз – в течение 5-ти – 10-ти минут. Время измерения задаётся преподавателем. Результаты измерений и их обработки занести в табл.1. Объяснить, почему при увеличении времени измерения активности нуклида ошибка уменьшается.

5. Этот же препарат подвергнуть измерению по 2-10 раз в серии, в течение 1 минуты, 2-5 минут,5-10 минут. Количество измерений в сериях и время от­дельных измерений задаются преподавателем. Результаты каждой серии изучения активности препарата обработать и занести в табл. 2.

6. Измерить скорость счета для одного или нескольких препаратов с различными степенями точности, то есть с разными относительными ошибками – от 0,01 до 0,08, по указанию преподавателя. Необходимое для измерения время рассчитывается по формулам (2.18) или (2.19) с учетом рекомендаций по их применению. На основании произведенных измерений рассчитать абсолютные и относительные ошибки по формулам (2.12) и (2.13). Результаты обсудить с преподавателем и принять меры к устранению возможных ошибок. Для скорости счета записать выражение в виде (2.20) или (2.21).

Таблица 1(пример).

№ измер.	Время отд. измер.t, мин	Число импуль- cов n	Скорость cчёта J=n/t	JА=JА+Ф-JФ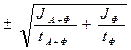

Вывод: среднквадратическая ошибка скорости счёта импульсов уменьшается с увеличением времени измерения.

Таблица 2 (пример).

Время отд. измер. t, мин.	Число имп. ni за t мин. одного изм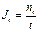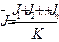.	, имп/мин	имп/мин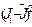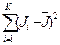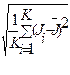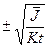

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Широков Ю.М., Юдин Н.П. Ядерная физика. М.: Наука, 1980.-727с.

2. Лабораторные занятия по физике / Под ред. Гольдина Л.Л. –М.: Наука, 1983.-704с.

3. Абрамов А.И., Казанский Ю.А., Матусевич Е.С. Основы экспериментальных методов ядерной физики. М.: Энергоатомиздат, 1985.-488с.

4. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Основы моделирования и первичная обработка данных. М.: Финансы и статистика, 1983. 471 с.

5. Сквайрс Дж. Практическая физика. М.: Мир, 1971. 248 с.

6. Худсон Д. Статистика для физиков. М.: Мир, 1970. 296 с.

Контрольные вопросы

1. Дайте определение постоянной распада и активности нуклида. В каких единицах измеряется активность?

2. Дайте определения основных дозиметрических единиц.

3. Сформулируйте основной закон радиоактивного распада.

4. Дайте определение периода полураспада и среднего времени жизни. Как связаны эти величины между собой?

5. Докажите, что вероятность распада характеризуется распределением Пуассона.

6. Как определяется средняя активность препарата, дисперсия, среднеквадратичное отклонение и относительная ошибка?

7. Как связаны между собой активность нуклида и скорость счёта импульсов счётчика?

8. Почему поток регистрируемых импульсов счётчика подчиняется статистике Пуассона?

9. Какие ошибки возникают при измерении активности нуклида и чем они вызваны?

10. Что называется среднеквадратической ошибкой и от чего она зависит?

11. Как можно оценить ошибку при измерении активности припарата?

12. Как фон влияет на точность измерений?

13. Какими способами можно уменьшить ошибки, возникающие при измерении активности нуклида?

14. Что называется среднеквадратической ошибкой среднего арифметического и от чего она зависит?

15. Как определить время, необходимое для измерения активности нуклида с заданной степенью точности?

16. Что характеризует величины, стоящие в предпоследнем и последнем столбцах табл.2?