Mechanical free damped oscillations
THE AIM is to determine the logarithmic decrement and the damping factor of mechanical oscillations.
INSTRUMENTATION AND APPLIANCES: spring pendulum, stopwatch, set of loads.
Short theory
Oscillatory motion of mechanical system, as a rule, occurs in the presence of friction, resulting in the transformation of mechanical energy of oscillations into heat. Ideal oscillations will continue for ever without change in amplitude. Friction, however, produces damped oscillations. In this case it is possible to write the displacement equations in the form
x = Acoswt, (18.1)
but A is understood to decrease with time.
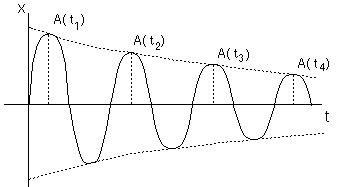
Figure 18.1
To determine in what a way A(t) depends on time, the frictional force must be known for every instant of time during which oscillations occur. A simplifying assumption is that the frictional force is proportional to the velocity of motion
ffr= - r v (18.2)
where the coefficient r is known as the resistance constant.
In the presence of friction the oscillating body is under the action of two forces:
restoring force
F = - kx = - m w02x (18.3)
and the force of friction
ffr= - r v (18.4)
Applying Newton's second law we obtain:
ma = - kx - r v (18.5)
By substitution, it is not difficult to show that this equation is satisfied by the equation
x = A0e- (r/2m) tcoswt . (18.6)
Here, A0 is the amplitude at the instant of time t = 0.
It should be noted that the ratio of two successive amplitudes is a constant. Thus, the expressions for the amplitude after (n – 1) and n periods, respectively, are
An-1= A0e- [r/2m](n-1) T (18.7)
An = A0e- [r/2m] n T
Let as divide the former relation by the latter. The ratio
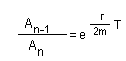 (18.8)
(18.8)
does not depend on n. The rate of damping is sometimes expressed by the logarithmic decrement λ
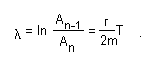 (18.9)
(18.9)
Calculate the velocity and acceleration of motion expressed by the formula
 (18.10)
(18.10)
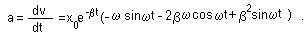 (18.11)
(18.11)
Then we obtain
( -mw2 +mb2 + k - rb ) sinw t + ( 2mbw - rw ) cosw t = 0
This equation holds good at any instant (at any combinations of sinw t and cosw t), which is possible if the coefficients before sine and cosine equal zero. Then
2mb =r ; m(w2 + b2 ) = k = mw02;
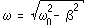 (18.12)
(18.12)
Here ω is the frequency of damped oscillations.
Experimental part

The damping factor is
 (18.13)
(18.13)
1. Make the spring pendulum in oscillation motion.
2. Measure the amplitudes of first - A1 and of fifths - A5 oscillations.
3. Calculate the period of vibration by the formula
T = t/n , (18.14)
where t is the time of "n" oscillations ; "n" is the number of oscillations.
4. Calculate the logarithmic decrement and the damping factor in accordance with the relations
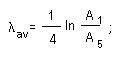 (18.15)
(18.15)
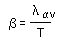 (18.16)
(18.16)
5. Calculate Dl/l , Db/b , Dl and Db for five measurements. Calculate the half-width of the confidence interval for A1 ,A5 and t using the main errors of measurements.
6. Put down the date of measurements and the results of calculation in the table 1.
7. Repeat the measurements for another mass.
8. Put down the date of measurements in table 1.
9. Make analyses of the experimental results.
Table 18.1
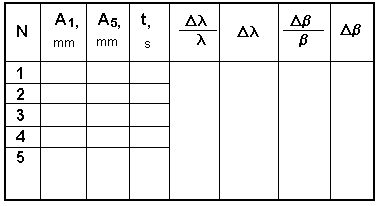
Control questions
1. What oscillations is damped?
2. Write down differential equation of damped oscillations and specify physical value.
3. What law does displacement of damped oscillations change on from time? Write equation of damped oscillations and draw its graph.
4. How does amplitude of damped oscillations depend from time?
5. Give determination and write down expression for logarithmic decrement.
6. What is named times of relaxation?
Translator: S.P. Lushchin, the reader, candidate of physical and mathematical sciences.
Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.
Approved by the chair of physics. Protocol № 6 from 30.03.2009 .
ЛАБОРАТОРНА РОБОТА № 45
ДОСЛІДЖЕННЯ ЗАТУХАЮЧИХ ЕЛЕКТРОМАГНІТНИХ КОЛИВАНЬ У КОЛИВАЛЬНОМУ КОНТУРІ
Мета роботи: дослідити затухаючі електромагнітні коливання у коливальному контурі.
Завдання: визначити характеристики затухаючих коливань: коефіцієнт затухання; логарифмічний декремент; час релаксації;добротність.
Теоретична частина
Електричне коло, яке складається з конденсатора 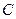 та котушки
та котушки 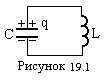 індуктивності
індуктивності  , називається коливальним контуром (рис.19.1). Надамо конденсатору певний заряд
, називається коливальним контуром (рис.19.1). Надамо конденсатору певний заряд 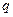 . Конденсатор, замкнений на
. Конденсатор, замкнений на
котушку індуктивності, почне розряджатись, у колі потече електричний струм  . Енергія електричного поля конденсатора:
. Енергія електричного поля конденсатора: 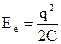 переходить в енергію магнітного поля котушки:
переходить в енергію магнітного поля котушки: 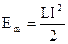 . Після повної розрядки конденсатора, енергія його електричного поля перейде в енергію магнітного поля котушки. Після чого конденсатор почне перезаряджатись, енергія магнітного поля котушки переходить у енергію електричного поля конденсатора і т. д. Таким чином у коливальному контурі відбуваються взаємні перетворення електричної та магнітної енергій, тобто, виникають електромагнітні коливання.
. Після повної розрядки конденсатора, енергія його електричного поля перейде в енергію магнітного поля котушки. Після чого конденсатор почне перезаряджатись, енергія магнітного поля котушки переходить у енергію електричного поля конденсатора і т. д. Таким чином у коливальному контурі відбуваються взаємні перетворення електричної та магнітної енергій, тобто, виникають електромагнітні коливання.
Будь-яке реальне електричне коло має активний опір 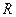 , на якому відбувається розсіювання енергії за рахунок його нагрівання.. Окрім того, частина енергії витрачається на випромінювання. В результаті енергія коливального контуру з часом зменшується і коливання будуть затухати.
, на якому відбувається розсіювання енергії за рахунок його нагрівання.. Окрім того, частина енергії витрачається на випромінювання. В результаті енергія коливального контуру з часом зменшується і коливання будуть затухати.
Для дослідження затухаючих електромагнітних коливань складається електричне коло, схема якого показана на рис.19.2. Синусоїдальний сигнал, що надходить від джерела 1, після проходження через  діод 2 випрямляється і набуває виду (рис.19.3,б). Таким чином з частотою 50 Гц конденсатор коливального контуру періодично одержує певний заряд
діод 2 випрямляється і набуває виду (рис.19.3,б). Таким чином з частотою 50 Гц конденсатор коливального контуру періодично одержує певний заряд  . Піс
. Піс
 |
ля одержання конденсатором цього заряду, в контурі розпочинаються затухаючі коливання. Диференціальне рівняння затухаючих коливань можна одержати з другого закону Кірхгофа, за яким сума падінь напруги на всіх елементах контуру дорівнює сумі е.р.с., що містяться в цьому контурі:
 (19.1)
(19.1)
У даному випадку маємо:
 (19.2)
(19.2)
де  - падіння напруги на активному опорі контуру;
- падіння напруги на активному опорі контуру;  - напруга на конденсаторі;
- напруга на конденсаторі;  - Е.Р.С. самоіндукції. З рівняння (19.2) одержуємо:
- Е.Р.С. самоіндукції. З рівняння (19.2) одержуємо:
 (19.3),
(19.3),
або
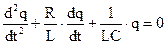 (19.4)
(19.4)
У формулі (19.4) позначимо через:
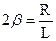 ;
; 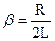 (19.5)
(19.5)
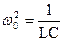 ;
;  (19.6)
(19.6)
З формули (19.6) для періоду вільних коливань у коливальному контурі одержуємо:
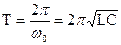 (19.7)
(19.7)
Величина 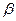 називається коефіцієнтом затухання. З використанням формул (19.5), (19.6) рівняння (19.4) набуває виду:
називається коефіцієнтом затухання. З використанням формул (19.5), (19.6) рівняння (19.4) набуває виду:
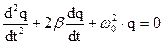 (19.8)
(19.8)
Рівняння (19.8) називається диференціальним рівнянням затухаючих коливань. Його розв’язок має вид:
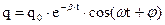 (19.9)
(19.9)
Таким чином, заряд, а також напруга на обкладинках конденсатора, зменшується з часом по експоненті  тим швидше, чим більший коефіцієнт затухання
тим швидше, чим більший коефіцієнт затухання 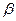 . Для амплітудних значень заряду на обкладинках конденсатора з формули (19.9) маємо:
. Для амплітудних значень заряду на обкладинках конденсатора з формули (19.9) маємо:
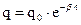 (19.10)
(19.10)
Час, на протязі якого заряд на обкладинках конденсатора зменшується в 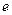 разів, називається часом релаксації. Час релаксації та коефіцієнт затухання є взаємо оберненими величинами:
разів, називається часом релаксації. Час релаксації та коефіцієнт затухання є взаємо оберненими величинами:
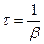 (19.11)
(19.11)
Відношення амплітуд коливань через період, 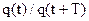 називається декрементом затухання, а натуральний логарифм цього відношення:
називається декрементом затухання, а натуральний логарифм цього відношення:
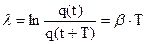 (19.12)
(19.12)
називається логарифмічним декрементомзатухання.
За час релаксації у контурі встигає відбутись певна кількість коливань 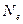 , яка дорівнює:
, яка дорівнює:
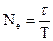 (19.13)
(19.13)
Величина:
 (19.14)
(19.14)
називається добротність. Добротність контуру тим більша, чим більша кількість коливань встигає відбутись у контурі за час релаксації.
Практична частина
1. Скласти та увімкнути в мережу схему, яка показана на рис.19.2.
2. 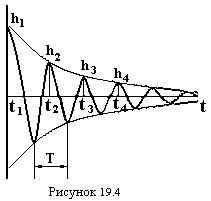 За допомогою потенціометрів “уровень” та ”стабильность”, які знаходяться на передній панелі осцилографа, одержати на екрані стійке зображення затухаючих коливань, яке показано на рис.19.4.
За допомогою потенціометрів “уровень” та ”стабильность”, які знаходяться на передній панелі осцилографа, одержати на екрані стійке зображення затухаючих коливань, яке показано на рис.19.4.
3. Визначити період коливань за формулою:
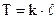 , (19.15)
, (19.15)
де: 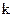 - коефіцієнт розгортки, а
- коефіцієнт розгортки, а 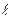 - відстань між двома сусідніми точками, які коливаються в одній фазі – рис. 19.4.
- відстань між двома сусідніми точками, які коливаються в одній фазі – рис. 19.4.
4. Висоти 
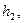
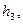 … на рис.19.4 пропорційні амплітудним значенням напруги та заряду на обкладинках конденсатора. Виміряти величини
… на рис.19.4 пропорційні амплітудним значенням напруги та заряду на обкладинках конденсатора. Виміряти величини 
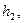
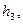 … та розрахувати відповідні моменти часу
… та розрахувати відповідні моменти часу 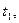
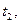
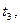 … за формулою:
… за формулою:
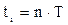 (19.16)
(19.16)
де 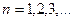 ; данні занести в таблицю 19.1.
; данні занести в таблицю 19.1.
Таблиця 19.1
 | 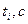 | 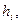 |  | 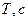 |  | 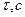 | 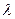 |  |
| … | ||||||||
5.  Побудувати графік залежності:
Побудувати графік залежності: 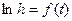 за зразком, який представлено на рис.19.5, тобто провести через експериментальні точки пряму лінію, яка б проходила якнайближче до кожної точки.
за зразком, який представлено на рис.19.5, тобто провести через експериментальні точки пряму лінію, яка б проходила якнайближче до кожної точки.
6. На графіку (але не з таблиці!) вибрати будь-які дві точки по яким знайти коефіцієнт
затухання  за формулою:
за формулою:
 (19.17)
(19.17)
За формулами (19.11), (19.12), (19.14) розрахувати величини  . Результати розрахунків занести в таблицю 19.1.
. Результати розрахунків занести в таблицю 19.1.
7.Помістити в котушку коливального контуру осердя і повторити вимірювання та розрахунки згідно пунктів 2 – 6. Данні занести в таблицю, аналогічну таблиці 19.1. Обидва графіки будувати на одній системі координат, а не окремо.
8. Порівняти данні двох таблиць та графіків. Зробити висновки.
Контрольні запитання
1. Які коливання називають затухаючими?
2. Записати диференціальне рівняння затухаючих коливань і вказати фізичний зміст величин, які входять у нього.
3. По якому закону змінюється зміщення затухаючих коливань з часом? Написати рівняння затухаючих коливань та намалювати його графік.
4. Як залежить амплітуда затухаючих коливань від часу?
5. Дати визначення і записати вираз для логарифмічного декремента затухання.
6. Що називається часом релаксації?
7. Який фізичний зміст логарифмічного декремента та коефіцієнта затухання?
8. Дати визначення добротності. Який її фізичний зміст?
9. Записати зв’язок між коефіцієнтом затухання і логарифмічним декрементом затухання.
Література
1. Сивухин Д. В. Общий курс физики. – т. 2. – М.: Наука, 1980, С.544-556.
2. Савельев И. В. Курс общей физики.– т. 2. – М.: Наука, 1982, С.251-258.
 Лабораторну роботу розробив доц. каф. фізики ЗНТУ
Лабораторну роботу розробив доц. каф. фізики ЗНТУ
Відредагував доц. каф. фізики ЗНТУ Правда М. І.
LABORATORY WORK № 45
