Т е м а 14-15. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ. ВОЛНОВОЕ УРАВНЕНИЕ. ПОЛЯРИЗАЦИЯ

ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ

ЭЛЕКТРОМАГНИТНЫХ ВОЛН

14.1. Покажите, что если электрическое поле зависит от времени t и координаты x (зависимости от y и z нет) в виде

,

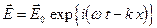то каждая компонента вектора напряженности удовлетворяет волновому уравнению.

14.2. Убедитесь, что вещественная часть 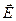описывает плоскую волну, распространяющуюся вдоль оси х. В какую сторону оси х распространяется волна?

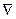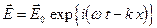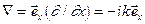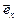14.3. Покажите, что если оператор действует на функции вида , то он имеет вид , где -единичный вектор вдоль оси х, . Можно ли подобное утверждать относительно оператора производной по времени?

14.4. Используя результат 14.3. покажите, какой вид имеют уравнения Максвелла для полей, зависящих от t и х синусоидально. Какая связь должна существовать между 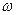и k?

14.5. Как изменятся ответы задач 14.1.-14.4., если электрическое поле имеет вид ?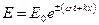

14.6. Две плоские монохроматические линейно поляризованные волны одной частоты распространяются вдоль оси z. Первая волна поляризована по x и имеет амплитуду а, вторая поляризована по y и имеет амплитуду b и опережает первую по фазе на 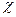. Найти поляризацию результирующей волны.

14.7. Рассмотреть в задаче 14.6. зависимость поляризации от сдвига фаз 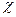для случая а=b.

14.8. Две монохроматические волны одной частоты поляризованы по кругу с противоположными направлениями вращения, имеют одинаковые фазы и распространяются в одном направлении. Амплитуда этих волн а (у правополяризованной волны) и b (у левополяризованной волны). Найти зависимость характера поляризации от а/b (а и b-вещественные).

15.1. Показать, что в плоской электромагнитной волне, распространяющейся в однородной среде, векторы 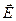и 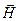взаимно перпендикулярны между собой и каждый из них перпендикулярен а направлению распространения волны. Показать также, что у плоской электромагнитной волны .

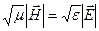15.2. Плоскополяризованная электромагнитная волна падает на границу раздела двух прозрачных сред 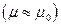с показателями преломления n₁ и n₂. Электрический вектор волны параллелен плоскости раздела сред. Найти коэффициент прохождения электромагнитной волны во вторую среду.

15.3. Показать для плоской монохроматической электромагнитной волны, что средняя по времени энергия, теряемая в волновой среде с удельной проводимостью 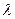, равна количеству выделившегося тепла.

15.6. Перпендикулярно к поверхности проводника с электропроводимостью 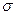и магнитной проницаемостью 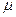падает плоская электромагнитная волна частоты 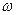. Пренебрегая токами смещения по сравнению с токами проводимости, определить, на какой глубине внутри проводника электромагнитное поле волны ослабевает в е раз (е-основание натуральных логарифмов).