Теорема оптимального кодирования источника

Независимых сообщений.

При заданном ансамбле 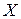из N независимых сообщений с энтропией 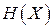возможно так закодировать сообщения ансамбля посредством последовательности символов, что среднее число символов на сообщение удовлетворяет неравенству

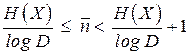,(3.1)

где 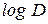- основание кода. Среднее число символов на сообщение 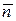не может быть сделано меньше, чем .

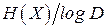Величина 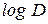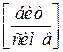- количество информации, приходящееся на один символ при кодировании кодом с основанием D. (При кодировании двоичным кодом 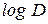=1)

Доказательство. Рассмотрим левую часть неравенства, составим разность 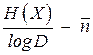и используем неравенство 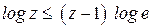, где знак равенства реализуется при z = 1.

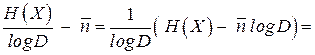
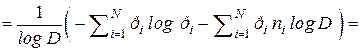
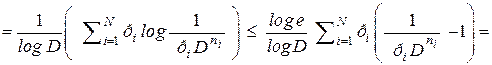
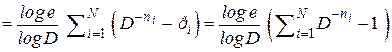. (3.2)

Рассмотрим разность 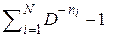. Пусть 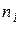- количество символов, употребляемых для кодирования 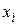-го сообщения, 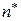- наибольшее количество символов, употребляемых для кодирования сообщения в ансамбле X. Число кодов, содержащих 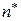символов, которое можно было бы создать, исходя из узла, состоящего из 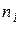символов, равно 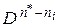. (Для иллюстрации этого предложения на рисунке 3.4 выделено сообщение 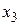, имеющий код 100, т. е. 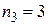. Наибольшее число символов 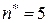на пятом уровне. На рисунке показаны ветви, исходящие из кода 100 на третьем уровне и останавливающиеся на пятом уровне. Число неиспользуемых кодов равно .)

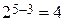Сумма всех неиспользуемых кодов не превышает числа кодов, образованных 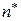разрядными кодами, т.е 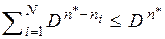или

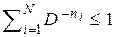(3.3)

Неравенство (3.3) называется неравенством Крафта. Используя неравенство Крафта, из (3.1) получим

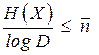. (3.4)

Знак равенства в (3.2) достигается тогда, когда

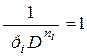. (3.5)

Из выражения (3.5) получим

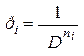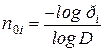, . (3.6)

Как видно из (3.6), чем меньше вероятность реализации события 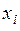, тем больше требуется символов для кодирования этого сообщения. Число символов 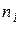- величина целая, но на практике при произвольной вероятности 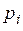получим дробную величину. Поэтому величину 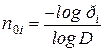округляют до ближайшего целого числа

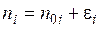, (3.7)

где .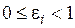

Умножим левую и правую части равенства (6) на 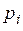и просуммируем полученное выражение

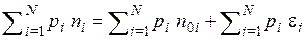. (3.8)

Положим, 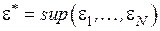.Тогда после соответствующих подстановок получим правую часть неравенства (3.1)

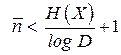. (3.9)

Как видно из неравенства (1) среде число символов, применяемое при кодировании, зависит от метода кодирования и распределения вероятностей реализации сообщений. Теорема не отвечает на вопрос, как оптимально кодировать сообщения, она показывает границы среднего числа символов.

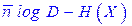- шум кодирования ???

Нет понятия скорости кодирования источника сообщений,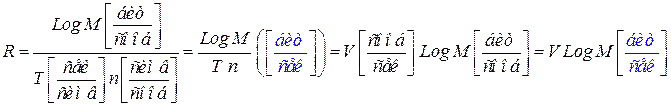

нет понятия ошибки кодирования и декодирования,

нет понятия скорости создания информации

Все это есть у Колесника (≈ Стр 36)

Канал связи

Под каналом связи понимается среда, в которой перемещается сигнал. В зависимости от типа сигнала каналы разделяются на непрерывные и дискретные.

Предполагается, что сигнал, передаваемый по каналу связи, дискретный как по времени, так и по своим состояниям, и сообщения, генерируемые источником, сжаты одним из методов кодирования, (хотя это не обязательно). Модель передачи информации изображена на рисунке 1.1.

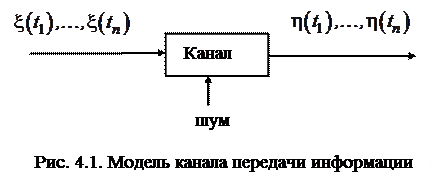Дискретный канал связи описывается ансамблем входных символов 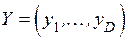с распределением вероятностей 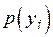, ансамблем выходных символов 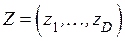и условными вероятностями 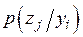= 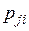перехода одного символа в другой. Условные вероятности составляют матрицу переходов

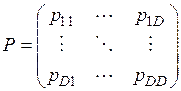(4.1)

Символы 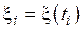, поступающие в канал связи в моменты времени 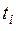выбраны из ансамбля Y, т.е. 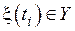. Обычно в канале связи действуют шумы, искажающие физические свойства сигналов, несущих информацию. В результате на выходе канала получают последовательность символов 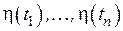таких, что 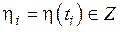. По своим свойствам канала связи классифицируется как

1) неоднородный канал с памятью - условная вероятность 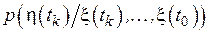получить символ 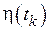в момент времени 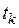зависит от некоторого множества символов поступивших на вход канала до момента времени 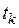. Неоднородность проявляется в том, что сохраняется зависимость условной вероятности от времени.

2) Неоднородный канал без памяти - условная вероятность 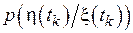не зависит от всех предыдущих символов на входе канала, но зависимость от времени остается

3) Однородный канал без памяти (стационарный канал) - условная вероятность 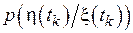не зависит от времени. В этом случае можно записать = .

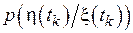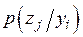В дальнейшем рассматривается стационарный канал.

Канал называется симметричным, если

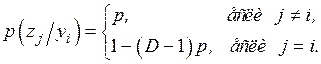
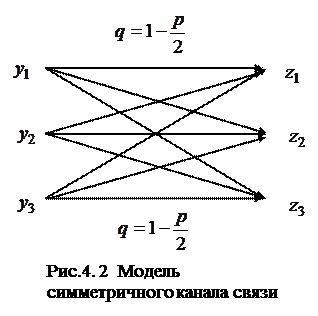
На рисунке 4.2 представлена модель симметричного канала с основанием кода

D = 3. На рисунке 4.3 изображена модель канала со стиранием.

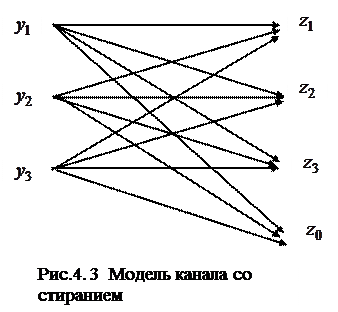
На практике при больших шумах часто нельзя отдать предпочтение тому или иному состоянию ансамбля Z. В этом случае в ансамбль Z вносится новое состояние

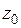. При переходе любого 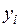в состояние 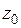должны быть предусмотрены какие-то действия, исключающие эту ошибку: стереть полученный символ, продублировать информацию и т. д. В этом случае имеем канал со стиранием.