Максимально возможная помехоустойчивость при заданном виде сигнала.

Котельников разработал теорию потенциальной помехоустойчивости. Он доказал, что для данного вида модуляции и данного вида помехи приемник обладает предельной помехоустойчивостью, превзойти которую нельзя. Эта помехоустойчивость называется потенциальной помехоустойчивостью. Потенциальная помехоустойчивость, на что впервые обратил внимание Котельников, зависит только от так называемой эквивалентной энергии сигналов. Помехоустойчивость выше (вероятность ошибки меньше) у той системы, у которой больше эквивалентная энергия используемых сигналов. Для определения такой возможной помехоустойчивости приема сигналов, определим среднюю вероятность ошибки при оптимальном приеме для ДЧМ сигнала:

p_ошЧМкг = 0,5× [1 – Ф(h₀)] = 0,067

10. Принятие решения приемником по трем независимым отсчетам.

Для повышения помехоустойчивости приёма дискретных двоичных сообщений, решение о переданном символе принимается не по одному отсчёту на длительности элемента сигнала 0 £ t £ T, а по трем некоррелированным отсчётам z(t₁)=9*10^-3 ,z(t₂)=5,4*10^-3, z(t₃)=9,9*10^-3 принимаемой смеси сигнала и помехи. Данный метод называется методом дискретного накопления. Для принятия решения о переданном символе, должна быть определена совместная трехмерная плотность распределения вероятностей для заданных трехотсчётов, т. е. W₃ (Z /1) и W₃(Z /0). Для случая гауссовского стационарного шума некоррелированные отсчёты смеси сигнала и шума будут независимыми. Следовательно, трехмерная плотность распределения вероятности будет равна произведению одномерных плотностей распределения каждого из отсчётов, т.е.

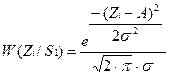
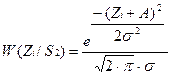
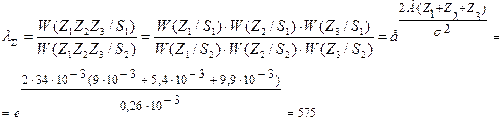
l0=0,33

Так как,l>l0 то в нашем случае принимается S₁.

11.Вероятность ошибки при использовании метода синхронного накопления.

При методе синхронного накопления суммируются k отсчетов (в нашем случае 3), взятых через интервал корреляции .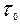

Рассмотрим физически преимущества и недостатки данного способа:

При суммировании k отсчетов полезный сигнал возрастает по амплитуде в k раз, а мощность накопленного сигнала увеличивается в 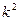раз. Помеха же суммируется со случайной фазами, в результате мощность помехи возрастает в k раз.

Т.е. 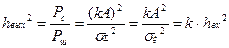и отношение мощность сигнал/шум увеличится в k (3) раза, следовательно вероятность ошибки уменьшится. При увеличении числа k вероятность ошибки еще уменьшится,но с ростом k скорость передачи будет уменьшатся.

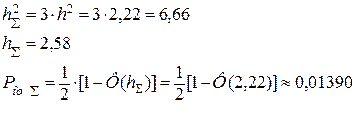
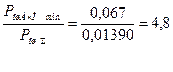
это означает, что помехоустойчивость при использовании данного метода увеличилась бы в 4,8 раз.

12.Применение импульсно-кодовой модуляции для передачи аналоговых сигналов.

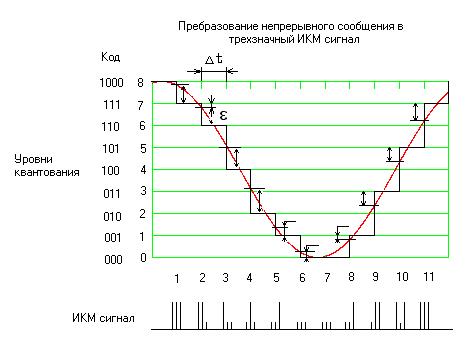
Рис 6. Принцип метода ИКМ

Сущность метода ИКМ заключается в передаче непрерывного сообщения в цифровой форме для этого на передающей стороне используется аналогово-цифровой преобразователь (АЦП) и для обратного преобразования на приемной стороне цифро-аналоговый преобразователь (ЦАП).

Преобразование аналог-цифра состоит из трех операции сначала непрерывное сообщение дискретизируется по времени через интервалы Dt, полученные отсчеты мгновенных значений квантуются, затем полученная последовательность квантованных значений непрерывного сообщения представляется посредством кодирования в виде последовательности кодовых комбинаций. Чаще всего кодирование сводится к записи номера уровня в двоичной системе счисления. При импульсно-кодовой модуляции (ИКМ) передача отдельных значений сигнала сводится к передаче определенных групп импульсов. Эти группы передаются друг за другом через относительно большие промежутки времени по сравнению с длительностью отдельных импульсов в линию связи. На приемной стороне линии связи последовательность импульсов после демодуляции и регенерации в приемнике поступает на ЦАП. В состав ЦАП входят декодирующее устройство, предназначенное для преобразования кодовых комбинации в квантованную последовательность отсчетов, и сглаживающий фильтр, восстанавливающии непрерывное сообщение по квантованным значениям.

К достоинствам ИКМ относится:

Основное техническое преимущество цифровых систем передачи перед непрерывными системами - их помехоустойчивость.

Широкое использование в аппаратуре преобразования сигналов современной элементной базы цифровой вычислительной техники и микроэлектроники.

Возможность приведения всех видов передаваемой информации к цифровой форме позволит осуществить интеграцию систем передачи и систем коммутации, а также расширить область использования вычислительной техники при построении аппаратуры связи и единой автоматизированной сети связи.

Недостатки ИКМ:Основным недостатком является то, что преобразование непрерывных сообщений в цифровую форму в системах ИКМ сопровождается округлением мгновенных значений до ближайших разрешенных уровней квантования.

Возникающая при этом погрешность преобразования является неустранимой, но контролируемой (так как не превышает половины шага квантования).

Произведем расчет мощности шума квантования и отношения сигнал/шум квантования h²_кв для случая поступления на вход приёмника сигнала с максимальной амплитудой.

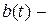непрерывное сообщение;

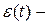погрешность квантования (шум квантования);

П = 3. - пик-фактор входного сигнала;

n =10 - число разрядов двоичного кода (при передаче сигналов методом ИКМ);

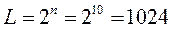- число уровней квантования;

b_max =5,6 в - максимальная амплитуда аналогового сигнала на входе АЦП;

Мощность шума квантования определяется поформуле ;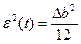

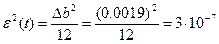, Вт – мощность шума квантования

;

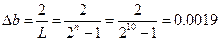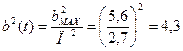Вт – мощность сигнала

Наидем соотношение сигнал/шум квантования по формуле: 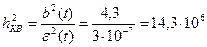; - это отношение мощности сигнала и мощности шума квантования h_кв при максимальной амплитуде аналогового сигнала.

Верность квантованного сообщения зависит от числа уровней квантования. Выбирая его достаточно большим можно уменьшить мощность шума квантования, до любой допустимой величины. Добавление каждого двоичного символа в кодовой комбинации (увеличение разрядности кода) улучшает отношение сигнал/шум приблизительно на 6 дБ. С другой стороны, увеличение разрядности требует повышения быстродействия многоразрядных кодирующих устройств, а также соответствующего расширения полосы частот канала передачи.

13.Использование сложных сигналов и согласованного фильтра.

Решение проблемы повышения помехозащищённости систем связи и управления достигается использованием различных методов и средств, в том числе и сигналов сложной формы (с большой базой).

Широкое практическое применение получили сложные сигналы на основе дискретных кодовых последовательностей, которые представляют собой последовательности символов длительностью Т, принимающих одно из двух значений: +1 или –1. Такие сигналы легко формируются и обрабатываются с использованием элементов цифровой и вычислительной техники.

Сложные сигналы должны удовлетворять ряду требований для достижения наибольшей достоверности их приёма:

а) корреляционная функция должна содержать значительный максимум (пик);

б) взаимная корреляционная функция любой пары сигналов из используемого ансамбля, определяющая степень их ортогональности, должна быть близка к нулю при любом t .

Влияние помехи в линии связи на передаваемый сигнал будет проявляться в изменении знака (полярности) элемента дискретного сигнала, т. е. в переходах вида 1 ® -1 и -1 ® 1. При приёме с помощью согласованного фильтра это будет приводить к изменению формы сигнала на его выходе – уменьшению основного лепестка, увеличению боковых выбросов и, следовательно, к снижению помехоустойчивости приёма. Поэтому целесообразно выбрать оптимальную величину порога решающей схемы приёмника, минимизирующую среднюю вероятность ошибки.

Форма сигналов S 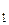(t)(1) и S 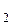(t)(0) при их передаче дискретной последовательностью будет выглядеть, как показано на рисунке 7.

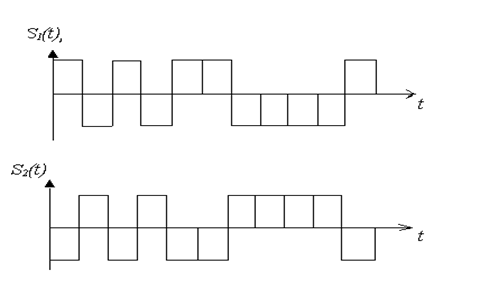Рис.7 Форма сигналов S 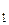(t)(1) и S 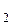(t)(0)

14.Импульсная характеристика согласованного фильтра.

Импульсная характеристика – есть отклик цепи на d-функцию.

; ;

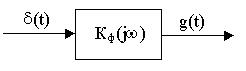
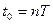
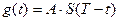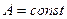Импульсная характеристика согласованного фильтра представляет собой зеркальное отображение S(t) с точностью до некоторого постоянного множителя и со сдвигом влево на величину Т.

Основным соотношением для оптимального фильтра считают импульсную характеристику, которая является зеркальным отображением сигнала S(t), сдвинутым на ве­личину t 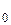.Импульсная характеристика приведена на рисунке

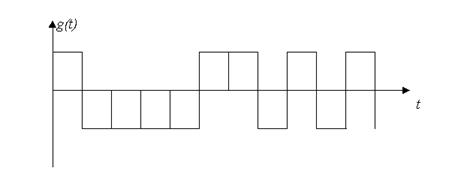
Рис.8 Импульсная характеристика согласованного фильтра

15.Схема согласованного фильтра для приема сложных сигналов. Форма сигналов на выходе согласованного фильтра при передаче символов "1" и "0".

Считаем, сто символы «1» и «0» передаются сложными сигналами S₁(t) S₂(t), которые представляют собой последовательности прямоугольных импульсов положительной и отрицательной полярности длительности Т. Приём этих сигналов осуществляется с помощью согласованного фильтра.

Дана дискретная последовательность из одиннадцати элементов:

1 -1 1 -1 1 1 -1 -1 -1 -1 1

Для этой последовательности нарисуем структурную схему приёмника с оптимальным фильтром, осуществляющего синхронный приём сообщений.

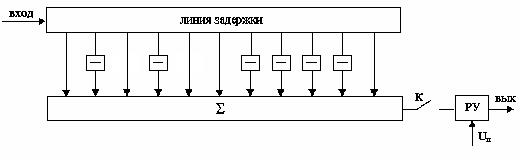
Рис.9 Структурная схема приёмника с оптимальным фильтром, осуществляющий синхронный приём сообщений

При синхронном приёме сообщений ключ К замыкается в области, когда передаваемая дискретная последовательность совпадает с последовательностью, на которую рассчитан фильтр. Поэтому на выходе максимальный сигнал, равный сумме амплитуд всех элементов сигнала. Значит для достижения помехоустойчивости U_п=0.

Структурная схема приёмника с оптимальным фильтром, осуществляющего асинхронный приём сообщений:

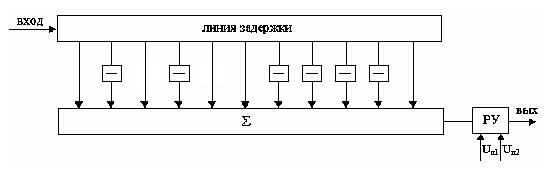
Рис.10 Структурная схема приёмника с оптимальным фильтром, осуществляющего асинхронный приём сообщений

При асинхронном приёме ключа нет, но в решающем устройстве выбираются 2 порога U_п1 и U_п2.На выходе согласованного фильтра получаем под дейст­вием сигнала функцию корреляции сигнала, а под действием помехи функцию взаимной корреляции сигнала и помехи. Если на входе фильтра только помеха (без сигнала), на выходе получаем только функцию взаимной корреляции по­мехи и сигнала, с которым, фильтр согласован. Если на вход согласованного фильтра поступает флуктуационная помеха,

то теоретически функция взаимной корреляции В 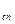должна быть равна нулю, так как сигнал и помеха являются независимыми функциями времени. Однако ва практике В 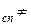0, так как при вычислении функции взаимной корреляции требуется бесконечно большое время интегрирования. В нашем же случае интегрирование ведется за время, равное Т.

Известно, что сигнал на выходе согласованного фильтра в произвольный момент времени характеризуется интегралом свёртки вида

,

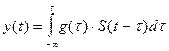где g(t) – импульсная характеристика фильтра.

Выходной сигнал согласованного фильтра совпадает по форме с функцией корреляции входного сигнала, т.е.

y(t) = a×K_ss (t - t₀),

где a – множитель пропорциональности;

t₀ – сдвиг в сторону запаздывания.

На практике величину t₀ выбирают равной длительности сигнала,
т.е. t₀ = T_с.

Для корреляционной функции дискретного сигнала общего вида применима формула

,

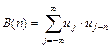здесь n указывает количество элементов, на которое осуществляется сдвиг исходного дискретного сигнала (n – целое число, положительное, отрицательное или нуль), так как важнейшей операцией при корреляционной обработке дискретных сигналов с использованием согласованного фильтра является поэлементный сдвиг такого сигнала.

Взаимная корреляционная функция двух дискретных сигналов по аналогии с корреляционной функцией одиночного сигнала определяется формулой

.

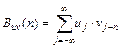Расчитаем форму сигнала на выходе согласованного фильтра при приеме сигнала согласованного с ним .

u ={1, -1, 1, –1, 1, 1, -1, -1, -1, -1, 1} , v = {1, -1, 1, –1, 1, 1, -1, -1, -1, -1, 1} .

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n = 0 v.. . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1 . .

Рез-т перемнож. = 1 1 1 1 1 1 1 1 1 1 1

Рез-т суммиров. В_uv (0) = 11.

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n = 1 v.. . 0 1, -1, 1,-1, 1, 1, -1, -1, -1, -1 . .

Рез-т перемнож. = 0 -1 -1 -1 -1 1 -1 1 1 1 -1

Рез-т суммиров. В_uv (1) = -2.

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n = 2 v.. . 0 0 1, -1, 1,-1, 1, 1, -1, -1, -1 . .

Рез-т перемнож. = 0 0 1 1 1 -1 -1 -1 1 1 -1

Рез-т суммиров. В_uv (2) = 1.

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n = 3 v.. . 0 0 0, 1, -1, 1, -1, 1, 1, -1, -1 . .

Рез-т перемнож. = 0 0 0 -1 -1 1 1 -1 -1 1 -1

Рез-т суммиров. В_uv (3) = -2

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n = 4 v.. . 0 0 0, 0 1, -1, 1, -1, 1, 1, -1 . .

Рез-т перемнож. = 0 0 0 0 1 -1 -1 1 -1 -1 -1

Рез-т суммиров. В_uv (4) = -3

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n = 5 v.. . 0 0 0, 0 0, 1, -1, 1, -1, 1, 1 . .

Рез-т перемнож. = 0 0 0 0 0 1 1 -1 1 -1 1

Рез-т суммиров. В_uv (5) = 2

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n = 6 v.. . 0 0 0, 0 0, 0, 1, -1, 1, -1, 1 . .

Рез-т перемнож. = 0 0 0 0 0 0 -1 1 -1 1 1

Рез-т суммиров. В_uv (6) = 1

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n =7 v.. . 0 0 0, 0 0, 0, 0, 1, -1, 1, -1 . .

Рез-т перемнож. = 0 0 0 0 0 0 0 -1 1 -1 -1

Рез-т суммиров. В_uv (7) = -2

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n =8 v.. . 0 0 0, 0 0, 0, 0, 0, 1, -1, 1 . .

Рез-т перемнож. = 0 0 0 0 0 0 0 0 -1 1 1

Рез-т суммиров. В_uv (8) = 1

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n =9 v.. . 0 0 0, 0 0, 0, 0, 0, 0 1, -1 . .

Рез-т перемнож. = 0 0 0 0 0 0 0 0 0 -1 -1

Рез-т суммиров. В_uv (9) = -2

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n =10 v.. . 0 0 0, 0 0, 0, 0, 0, 0, 0, 1 . .

Рез-т перемнож. = 0 0 0 0 0 0 0 0 0 0 1

Рез-т суммиров. В_uv (10) = 1

u. . . 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1. . .

n =11 v.. . 0 0 0, 0 0, 0, 0, 0, 0, 0, 0 . .

Рез-т перемнож. = 0 0 0 0 0 0 0 0 0 0 0

Рез-т суммиров. В_uv (11) = 0

Т.к. функция корреляции не зависит от направления сдвига то график можно зеркально отразить.

График сигнала на выходе фильтра представлен на рис.11

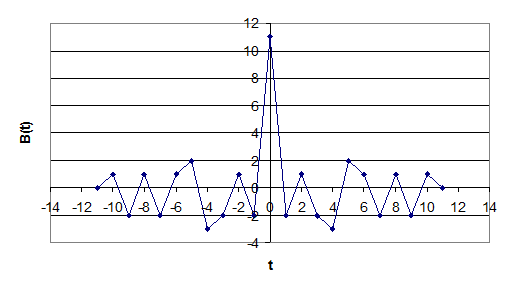
Рис.11 Форма сигнала на выходе согласованного фильтра при приеме сигнала согласованного с ним.